What is Escape Velocity? How do we go to other Planets?
TLDRThis script delves into the historical understanding of planetary orbits, moving from the geocentric model to the heliocentric model, and finally to Kepler's laws and Newton's law of gravitation. It explains the concept of escape velocity and how it relates to the trajectories of spacecraft, introducing the idea of conic sections and their relevance to the paths of celestial bodies. The lesson aims to provide a deeper understanding of the science behind the motion of planets and the technology we use to explore space.
Takeaways
- 🌌 Historical beliefs held that planetary orbits were perfect circles, a shape considered most perfect, but they are actually elliptical.
- 🚀 Escape velocity is the speed required for a spacecraft to break free from a planet's gravitational field and not return.
- 🪐 The concept of conic sections is crucial for understanding the different possible orbits around a planet, which can be a circle, ellipse, parabola, or hyperbola.
- 🔍 Early theories like the geocentric model by Ptolemy and the heliocentric model by Copernicus were later refined by Kepler's laws of planetary motion and Newton's law of gravitation.
- 📈 Newton's law of gravitation explains that every object in the universe attracts every other object with a force proportional to their masses and inversely proportional to the square of the distance between them.
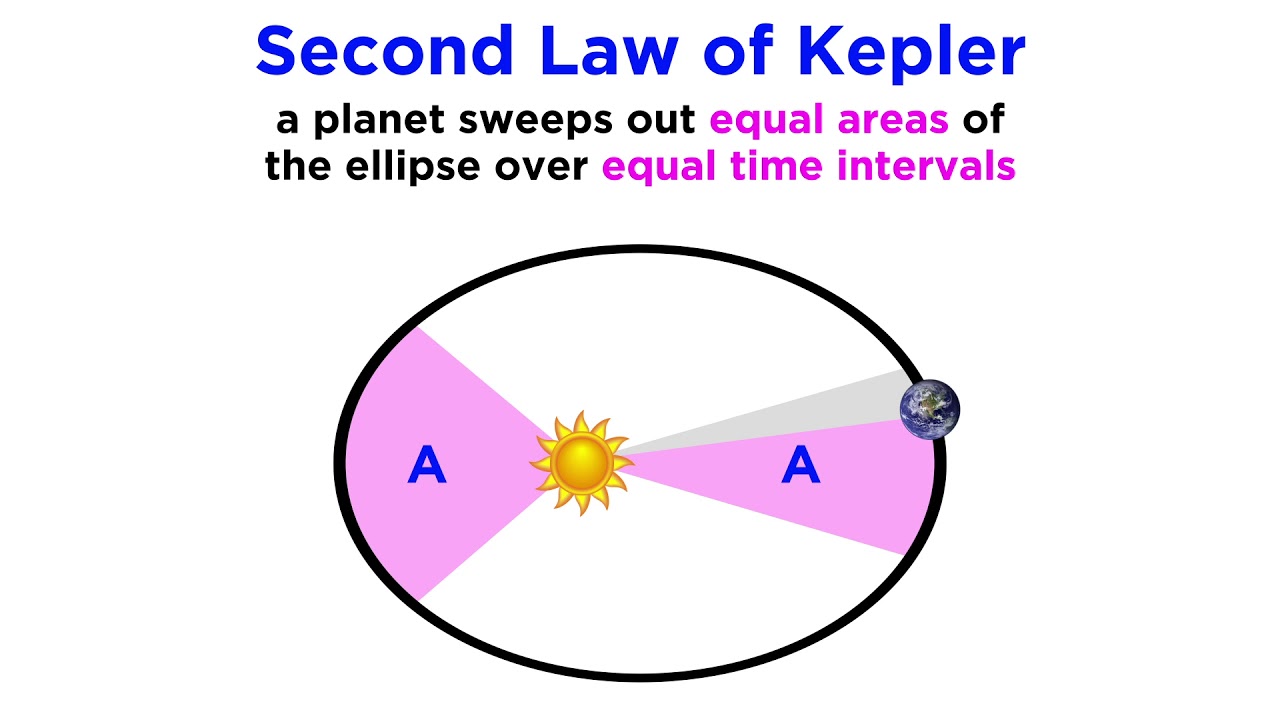
- 🌠 Kepler's first law states that planets move in elliptical orbits with the Sun at one of the foci, which was a significant departure from circular orbit theories.
- 💥 The escape speed varies for different celestial bodies. For Earth, it's about 11.2 km/s, the Moon's is 2.38 km/s, and Jupiter's is 59.5 km/s.
- 🛰️ Spacecraft trajectories are arcs because they follow the curvature of the planet due to gravity, and they cannot travel in a straight line when in the gravitational field.
- 🌞 The escape speed required to leave the Sun's gravitational influence is 618 km/s, a speed achieved by some spacecraft that will never return to our solar system.
- 📊 The study of planetary motion and the shapes of orbits is a triumph of scientific discovery, showing that the same force of gravity that holds objects on Earth also governs the celestial dance of the planets.
Q & A
What was the historical belief about the shape of planetary orbits?
-Historically, it was believed that the orbits of the planets were perfect circles, due to the idea that the circle was the most perfect shape.
What did Nicolaus Copernicus propose about the position of the Sun in the universe?
-Nicolaus Copernicus proposed the heliocentric model, which stated that the Sun was at the center of the universe and the planets revolved around it in circular orbits.
What significant observation did Johannes Kepler make about planetary orbits?
-Johannes Kepler observed that the orbits of the planets were not perfectly circular but elliptical in shape, leading to his formulation of the three laws of planetary motion.
How does Isaac Newton's law of gravitation relate to planetary orbits?
-Isaac Newton's law of gravitation shows that every object in the universe is attracted to every other object with a force proportional to the product of their masses and inversely proportional to the square of the distance between them. He applied this law to show mathematically that planets move in elliptical orbits around the Sun, with the Sun at one of the foci of the ellipse.
What is escape velocity and how does it apply to interplanetary travel?
-Escape velocity is the minimum speed needed for an object to break free from a planet's gravitational field and not fall back. It is crucial in interplanetary travel as spacecraft are sent on escape trajectories using this velocity to transition from one planet to another.
What is the escape speed for Earth?
-The escape speed for Earth is approximately 11.2 kilometers per second.
How does the shape of a spacecraft's orbit change with its speed?
-The shape of a spacecraft's orbit changes depending on its speed relative to the circular orbit speed. If the speed is less than the circular speed, the orbit is an ellipse. At the circular speed, the orbit is a circle. Above the circular speed but below the escape speed, the orbit is a larger ellipse. Exactly at the escape speed, the orbit is a parabola, and above the escape speed, it is a hyperbola.
What are the four types of conic sections and how are they related?
-The four types of conic sections are circles, ellipses, parabolas, and hyperbolas. They are related because all of these shapes can be obtained by slicing a cone in different ways.
How does the shape of a parabola relate to the slicing of a cone?
-A parabola is formed by slicing a cone parallel to its side, resulting in a shape that opens upwards with a rounded bottom and a single curve.
What is the significance of conic sections in astronomy?
-Conic sections are significant in astronomy because they describe the different possible shapes of orbits that celestial bodies can have around a gravitational center, such as planets orbiting a star.
What happens to a spacecraft's trajectory if it exceeds the escape velocity?
-If a spacecraft exceeds the escape velocity, its trajectory becomes a hyperbola. This means it will move away from the gravitational field indefinitely and will not return.
Outlines
🌌 Historical Understanding of Planetary Orbits
This paragraph delves into the historical conception of planetary orbits, starting with the belief that they were perfect circles, a notion challenged by later scientific discoveries. It discusses the evolution of astronomical theories from the geocentric model of Ptolemy to the heliocentric model of Copernicus, and finally to Kepler's laws of planetary motion which revealed that orbits are elliptical. The paragraph also touches on the role of Isaac Newton's law of gravitation in explaining these orbits.
🚀 The Concept of Escape Speed and Orbital Trajectories
This section introduces the concept of escape speed, the speed required for a spacecraft to break free from a planet's gravitational pull and not return. It explains how the velocity of a spacecraft determines the shape of its orbit, transitioning from circular orbits to elliptical paths and finally to parabolic or hyperbolic trajectories as velocity increases. The paragraph also provides specific escape speed values for Earth, the Moon, Jupiter, and the Sun, emphasizing the vast difference in these speeds based on the gravitational pull of each celestial body.
🌍 Gravity's Role in Shaping Orbits
The paragraph discusses the influence of gravity on the shape of planetary orbits, from the early belief in circular orbits to the understanding that orbits are conic sections—circles, ellipses, parabolas, or hyperbolas—based on the velocity of the orbiting body. It explains how gravity, although always pulling an object downward, can result in circular orbits if the object moves fast enough. The paragraph also introduces the concept of circular orbit speed, different from escape speed, which is the velocity needed to maintain a stable orbit around a planet.
🌟 The Transformation of Shapes through Varying Energy Levels
This part of the script explores how varying energy levels result in different conic sections. It explains that at low energy levels, orbits are circular, and as energy increases, they become elliptical. At the exact escape velocity, the orbit is a parabola, and beyond that, a hyperbola. The paragraph visually describes the transition from circles to ellipses, parabolas, and hyperbolas, emphasizing the mathematical and physical principles behind these transitions.
📐 The Origin of Conic Sections
The paragraph introduces the concept of conic sections, explaining that all these shapes—circles, ellipses, parabolas, and hyperbolas—originate from slicing a cone in different ways. It describes the process of obtaining a circle by slicing a cone perpendicular to its base and an ellipse by slicing at an oblique angle. The section also touches on the historical significance of these shapes and sets the stage for a deeper exploration of their mathematical properties and applications in future lessons.
🌐 Application of Conic Sections in Astronomy
This paragraph ties the concept of conic sections to the real-world application of planetary orbits, explaining how the energy levels of celestial bodies determine the type of conic section their orbit follows. It mentions the transition from small ellipses to circles and then to larger ellipses, parabolic trajectories at escape velocity, and hyperbolic trajectories for objects moving faster than the escape velocity. The paragraph concludes by promising a deeper exploration of conic sections, their equations, and their applications in future lessons.
Mindmap
Keywords
💡Orbit
💡Escape Velocity
💡Conic Sections
💡Geocentric Model
💡Heliocentric Model
💡Johannes Kepler
💡Isaac Newton
💡Ellipse
💡Parabolic Trajectory
💡Hyperbolic Trajectory
Highlights
Introduction to planetary orbits originally thought to be perfect circles due to the aesthetic and philosophical preference for the shape.
Revelation that planetary orbits are elliptical, not circular, which corrected historical scientific misconceptions.
Discussion of escape velocity and its relevance in sending spacecraft from one planet to another.
Explanation of conic sections (circle, ellipse, parabola, hyperbola) as fundamental shapes describing orbits around a planet.
Historical context of the geocentric model by Ptolemy and its displacement by Copernicus' heliocentric model.
Johannes Kepler's development of his three laws of planetary motion based on elliptical orbits.
Isaac Newton's formulation of the universal law of gravitation, explaining the elliptical orbits of planets mathematically.
Practical demonstrations of how different velocities affect the trajectory of a thrown object, leading to different orbital shapes.
The concept of different orbital speeds, including the specific escape speeds for Earth, the Moon, and Jupiter.
Illustration of how spacecraft achieve and exceed escape velocity, permanently leaving the Earth's or another celestial body's gravitational field.
The role of velocity in determining the specific type of orbit (circular, elliptical, parabolic, hyperbolic).
Introduction to the conic sections derived from cutting a cone at different angles.
Explanation of how the shapes of orbits (ellipse, parabola, hyperbola) correspond to different energy levels and velocities.
Discussion on the implications of conic sections in understanding the universe's structure and the motion of celestial bodies.
Summary of how ancient astronomers' observations led to the modern understanding of orbits as not merely circular but complex conic sections.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: