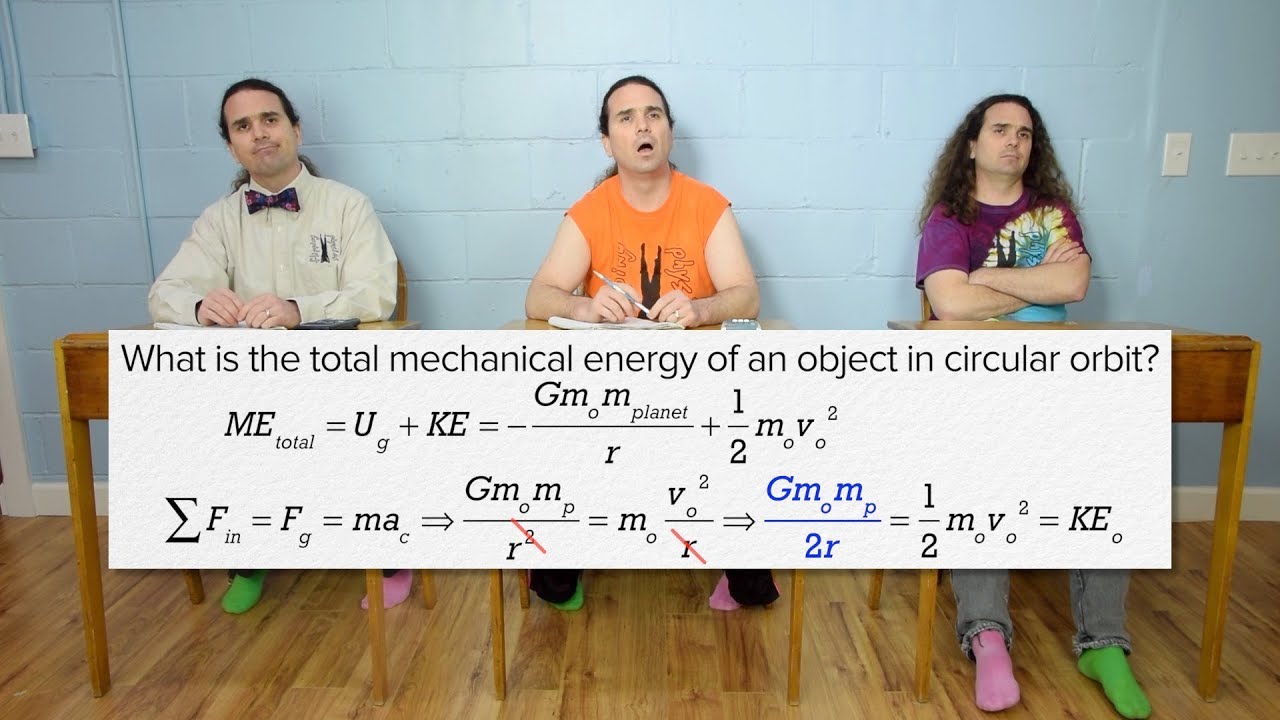Kepler's Laws
TLDRThe transcript discusses Johannes Kepler's laws of planetary motion, which revolutionized the understanding of how planets orbit the sun. Kepler's first law states that planets move in elliptical orbits with the sun at one focus. The second law reveals that a planet sweeps out equal areas in equal times, indicating varying speeds along its orbit. The third law connects a planet's orbital period to its semi-major axis, expressed as the period squared being proportional to the semi-major axis cubed. These laws were derived from Newton's universal law of gravitation, highlighting the interconnected nature of celestial bodies in our solar system.
Takeaways
- 🌞 Kepler's First Law: Planetary orbits are elliptical with the Sun at one of the two foci, marking a shift from the previous belief in circular orbits.
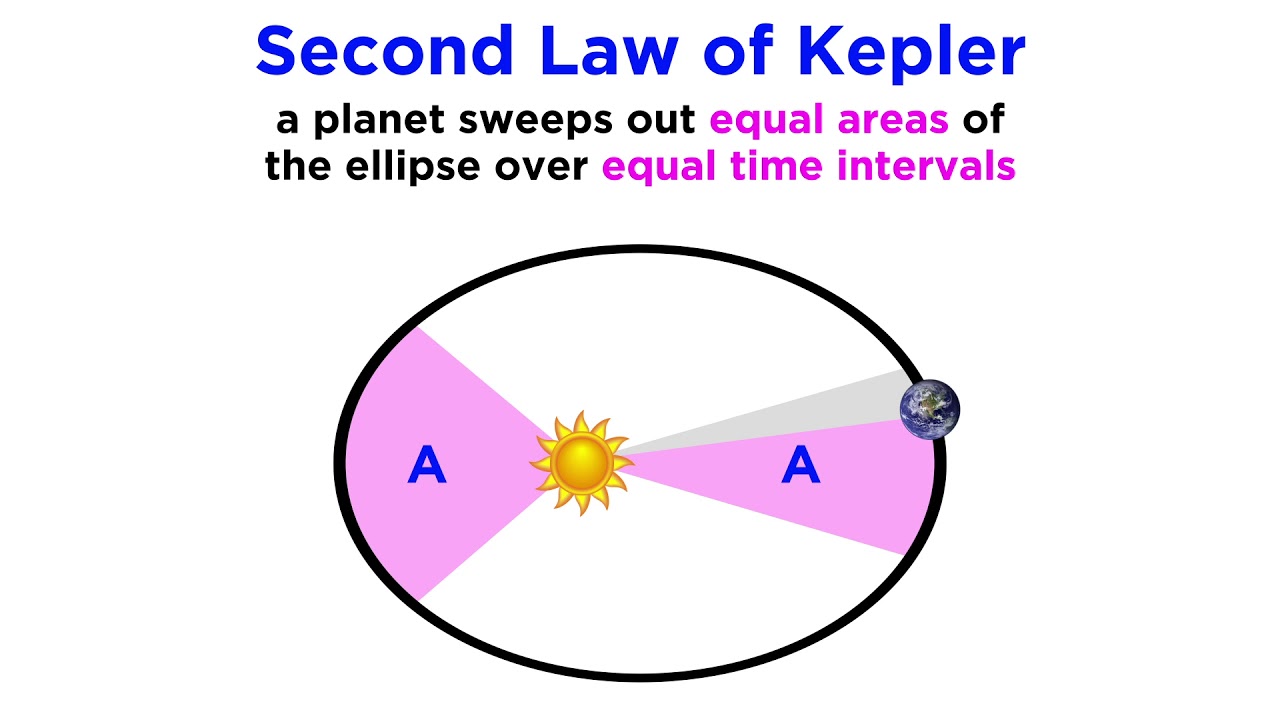
- 📐 Kepler's Second Law: A planet sweeps out equal areas in equal times, indicating that planets move faster when they are closer to the Sun (perihelion) and slower when they are farther away (aphelion).
- 🔢 Kepler's Third Law: The square of a planet's orbital period is proportional to the cube of the semi-major axis of its orbit, providing a mathematical relationship between these two parameters.
- 💫 Johannes Kepler built upon Tycho Brahe's data to develop these laws, enhancing the understanding of planetary motion.
- 🌌 The laws apply to all objects in orbit around the Sun, not just Earth, including other planets and comets like Halley's Comet which has an orbital period of about 76 years.
- 📈 The eccentricity of an orbit describes how 'circular' or 'elliptical' it is; low eccentricity indicates a near-circular orbit, while high eccentricity indicates a highly elliptical orbit.
- 🌠 Halley's Comet, with its high eccentricity, has a long period and is visible from Earth approximately every 76 years.
- 🔗 Newton's Universal Law of Gravitation can be used to derive Kepler's Laws, unifying the understanding of the solar system's dynamics under one law.
- 🌍 Earth's orbit is nearly circular with a low eccentricity, while the orbits of other planets can vary significantly in their eccentricity.
- 🔄 The gravitational force between two masses (like a planet and the Sun) is given by the formula F = G * (m1 * m2) / r^2, where G is the gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the two masses.
- 📊 Kepler's Third Law can be mathematically expressed as T^2 ∝ a^3, where T is the orbital period and a is the semi-major axis, leading to the concept of the Kepler constant (k_s).
Q & A
Who was Johannes Kepler's employer and what was his contribution to astronomy?
-Johannes Kepler was employed by Tycho Brahe, who collected extensive data on the universe, stars, and planetary motions. Brahe's work laid the foundation for Kepler's later achievements in understanding planetary orbits.
What was the prevailing belief about planetary orbits before Kepler's laws?
-Before Kepler's laws, it was commonly believed that planetary orbits were circular due to the near-circular appearance of Earth's orbit around the Sun.
What is the first of Kepler's laws and how does it challenge previous beliefs?
-The first of Kepler's laws states that orbits are elliptical, with the Sun at one of the two foci. This challenged the previous belief of circular orbits by showing that while Earth's orbit is nearly circular, other planets have more eccentric orbits.
Explain Kepler's second law in simple terms.
-Kepler's second law, also known as the law of equal areas, states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This implies that a planet moves faster when it is closer to the Sun and slower when it is farther away.
How does Kepler's third law relate the orbital period of a planet to its orbit's shape?
-Kepler's third law states that the square of a planet's orbital period is directly proportional to the cube of the semi-major axis of its orbit. This means that the larger the semi-major axis (or the wider the orbit), the longer the planet's year.
What is the significance of Newton's universal law of gravitation in relation to Kepler's laws?
-Newton's universal law of gravitation is significant because it allows for the derivation of all of Kepler's laws. It unified the understanding of the solar system by explaining the motion of all planets with a single law.
What is the relationship between a planet's eccentricity and its orbit shape?
-A planet's eccentricity is a measure of how much its orbit deviates from a perfect circle. Orbits with high eccentricity are more elongated (like that of Halley's comet), while low eccentricity indicates orbits that are nearly circular (like Earth's orbit).
How does the semi-major axis relate to the period of a planet's orbit?
-According to Kepler's third law, the period of a planet's orbit (the time it takes to complete one orbit around the Sun) is proportional to the cube of its semi-major axis (half of the major axis of the elliptical orbit).
What is the Kepler constant and how is it used?
-The Kepler constant (k_s) is a proportionality factor used in the formula that relates the period squared (T^2) to the semi-major axis cubed (a^3) of a planet's orbit. It has a specific value that applies to all celestial bodies in the solar system, allowing for the calculation of their orbital periods based on the size of their orbits.
How did the understanding of Kepler's laws contribute to the field of astronomy?
-Kepler's laws revolutionized astronomy by providing a mathematical description of planetary motion. They shifted the understanding from circular orbits to elliptical ones and established a fundamental relationship between a planet's orbital period and its distance from the Sun, which was later explained by Newton's law of gravitation.
What is the period of Halley's comet and when was the last time it was visible from Earth?
-Halley's comet has an orbital period of about 76 years. The most recent time it was visible from Earth was in 2016, and it will next appear in 2060.
Outlines
🌌 Kepler's Laws Explained
This segment introduces Johannes Kepler, who advanced the work of his mentor, Tycho Brahe, on understanding planetary orbits. Kepler formulated three laws from Brahe's comprehensive astronomical data. The first law posits that planetary orbits are elliptical with the Sun at one focus, challenging the then-prevailing notion of circular orbits. Kepler's second law, the law of equal areas, states that a planet covers equal areas in equal times along its orbit, implying that a planet's velocity varies, being fastest when nearest to the Sun. The third law establishes a relationship between the orbital period of a planet and the length of its semi-major axis, stating that the square of the period is proportional to the cube of the semi-major axis. This was a significant leap in understanding planetary motions and laid the groundwork for future astronomical theories.
🔭 From Kepler to Newton: Universal Gravitation
The second paragraph builds on Kepler's laws, emphasizing their validation through Isaac Newton's universal law of gravitation. It illustrates how Newton's work unified the celestial and terrestrial realms through a single physical law, a monumental achievement in science. The discussion elaborates on orbital eccentricity, with Earth's nearly circular orbit as a low-eccentricity example, contrasting with the highly eccentric orbit of Halley's Comet. This section also shares a personal anecdote about witnessing Halley's Comet, highlighting its 76-year orbit period, to underscore the practical implications of Kepler's third law and its derivability from Newton's formulations on gravity, thereby enriching the understanding of celestial mechanics.
🌠 Deriving Kepler's Third Law from Newtonian Mechanics
The final segment delves deeper into the mathematical derivation of Kepler's third law using Newton's laws of motion and universal gravitation. It explains how the gravitational force between the Sun and a planet results in circular motion, with the gravitational force providing the centripetal force necessary for the planet's orbit. By equating the gravitational force to the centripetal force and manipulating the equation, the narrative arrives at the formulation that the square of a planet's orbital period is proportional to the cube of its semi-major axis, exactly as Kepler had proposed. This mathematical journey not only solidifies the connection between Kepler's empirical laws and Newton's theoretical framework but also illustrates the predictive power of physics in understanding the cosmos.
Mindmap
Keywords
💡Kepler's Laws
💡Johannes Kepler
💡Tycho Brahe
💡Elliptical Orbits
💡Equal Areas in Equal Times
💡Period Squared
💡Semi-Major Axis
💡Eccentricity
💡Halley's Comet
💡Newton's Universal Law of Gravitation
💡Kepler Constant
Highlights
Johannes Kepler was Tycho Brahe's assistant and continued his work on understanding planetary orbits.
Kepler formulated three laws of planetary motion, now known as Kepler's Laws.
Kepler's First Law states that planetary orbits are elliptical with the Sun at one focus.
This was a significant departure from the previous belief in circular orbits.
Kepler's Second Law, also known as the Law of Equal Areas, states that a planet sweeps out equal areas in equal times.
This law implies that a planet moves faster when it is closer to the Sun and slower when it is farther away.
Kepler's Third Law relates the orbital period of a planet to its semi-major axis, stating that the period squared is proportional to the semi-major axis cubed.
Kepler's Laws were derived from Newton's Universal Law of Gravitation, tying the entire solar system together with one law.
Highly elliptical orbits are more eccentric, while near-circular orbits have low eccentricity.
Halley's Comet has a highly eccentric orbit and a period of about 76 years.
Kepler's Third Law can be derived from Newton's Law of Gravitation, showing a direct relationship between the period squared and the semi-major axis cubed.
The Kepler constant, k_s, is a specific value that applies to all celestial bodies in our solar system.
Kepler's Laws have practical applications, such as predicting the return of comets like Halley's Comet.
The transition from circular to elliptical orbit models was a significant scientific advancement.
The concept of gravitational slingshot is related to the varying speeds of a planet in its elliptical orbit.
Kepler's Laws are fundamental to understanding the motion of celestial bodies in our solar system and beyond.
The historical context of Kepler's work, building upon the observations of Tycho Brahe, highlights the importance of scientific collaboration and legacy.
The mathematical relationships in Kepler's Third Law provide a universal formula for the orbital periods of planets.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: