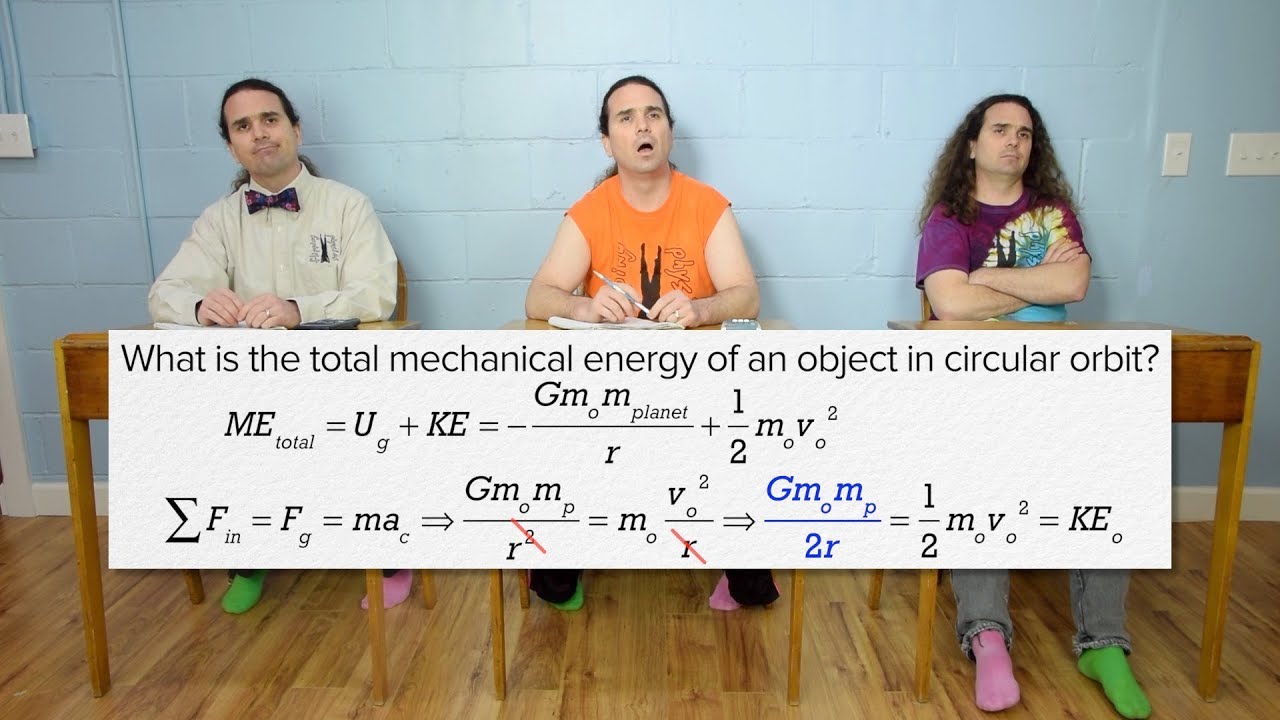AP Physics 1 - Kepler's Laws
TLDRIn this A+ Physics lesson, Dan Fullerton explains Kepler's laws of planetary motion, which describe the orbits of planets around the Sun. Kepler's first law states that planetary orbits are ellipses with the Sun at a focus. The second law, the Law of Equal Areas, indicates that a planet sweeps out equal areas in equal times. The third law connects the square of a planet's orbital period to the cube of its average orbital radius. These laws laid the foundation for Newton's Laws of Universal Gravitation and continue to be fundamental in understanding our solar system's dynamics.
Takeaways
- 📜 Kepler's Laws of Planetary Motion describe the orbits of planetary objects around the Sun, based on observations by German mathematician and astronomer, Johannes Kepler.
- 🥊 First Law: Planetary orbits are ellipses, with the Sun at one of the foci, indicating that planets move in a slightly oval-shaped path around the Sun.
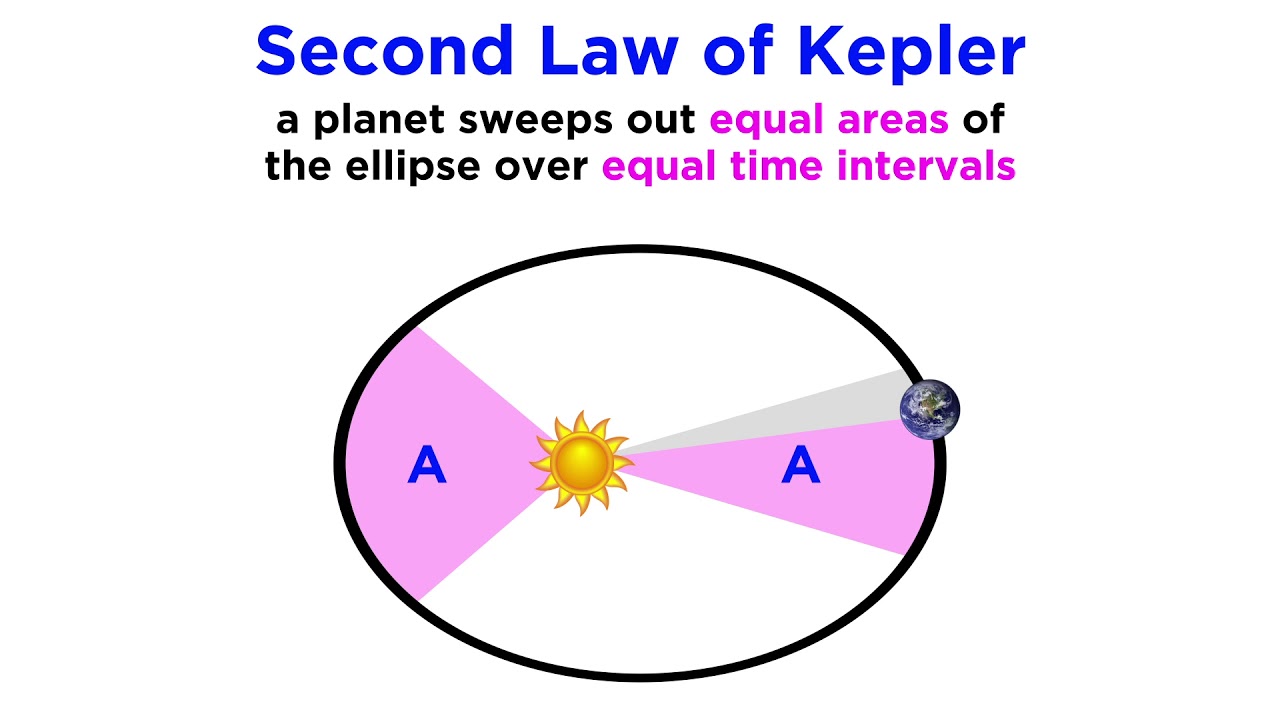
- 🏢 Second Law (Law of Equal Areas): A planet sweeps out equal areas in equal times, suggesting that the speed of a planet varies depending on its distance from the Sun, being fastest at the closest point (perihelion) and slowest at the farthest point (aphelion).
- 🔄 Third Law (Harmonic Law): The ratio of the squares of the periods of any two planets is equal to the ratio of the cubes of their average orbital radii. This law implies that planets closer to the Sun have shorter orbital periods than those farther away.
- 📈 Example Application: Mercury, being the closest planet to the Sun, has the shortest orbital period, which is approximately 0.24 Earth years, demonstrating the principles of Kepler's Third Law.
- 🌌 Conservation of Angular Momentum: The second law also reflects the conservation of angular momentum, meaning that the product of a planet's mass, velocity, and the sine of its orbital angle remains constant throughout its orbit.
- 🚀 Speed Variation: A planet's speed is greatest when it is closest to the Sun (perihelion) and least when it is farthest from the Sun (aphelion), as a result of the conservation of angular momentum.
- 🌠 Gravitational Potential Energy: The greatest gravitational potential energy occurs when a planet is at its farthest point from the Sun (aphelion), while the lowest potential energy corresponds to the closest point (perihelion).
- 🌐 Mars' Orbit: The shape of Mars' orbit around the Sun is most accurately described as an ellipse, in accordance with Kepler's First Law.
- 🌟 Kepler's Laws laid the groundwork for Isaac Newton's Laws of Motion and Universal Gravitation, significantly contributing to the Scientific Revolution in the 17th century.
Q & A
What are Kepler's laws of planetary motion?
-Kepler's laws of planetary motion are three fundamental rules that describe the orbits of planets around the Sun. They include the shape of the orbits (ellipses), the conservation of angular momentum (equal areas swept out in equal times), and the relationship between the squares of the periods of planets and the cubes of their orbital radii.
Who was Johann Kepler?
-Johann Kepler was a German mathematician and astronomer who lived in the late 16th and early 17th centuries. He is best known for his laws of planetary motion, which laid the groundwork for Isaac Newton's laws of universal gravitation and contributed significantly to the 17th-century Scientific Revolution.
What does Kepler's first law state?
-Kepler's first law states that the orbits of planetary bodies are ellipses, with the Sun at one of the foci of the ellipse. This means that planets move in a slightly elongated circular path around the Sun.
What is the significance of Kepler's second law, also known as the Law of Equal Areas?
-Kepler's second law, the Law of Equal Areas, states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This implies that the planet moves faster when it is closer to the Sun and slower when it is farther away, conserving angular momentum.
How does Kepler's third law relate the period of a planet's orbit to its distance from the Sun?
-Kepler's third law states that the ratio of the squares of the periods of two planets is equal to the ratio of the cubes of their average orbital radii. This means that planets closer to the Sun have shorter periods and thus orbit the Sun more quickly than planets that are farther away.
What is the role of angular momentum conservation in Kepler's second law?
-The conservation of angular momentum is a fundamental principle behind Kepler's second law. It states that in the absence of external forces or torques, the angular momentum of a system must remain constant. This is why planets move faster when they are closer to the Sun, as their linear speed increases to maintain the same angular momentum while moving in their elliptical orbits.
How does the shape of a planet's orbit affect its speed?
-According to Kepler's laws, the speed of a planet in its orbit is affected by its position in the orbit. A planet moves faster when it is closer to the Sun (perihelion) and slower when it is farther away (aphelion). This is due to the conservation of angular momentum and the shape of the elliptical orbit.
What is the relationship between a planet's distance from the Sun and its orbital period?
-According to Kepler's third law, the further a planet is from the Sun, the longer its orbital period. This is because the ratio of the square of the period to the cube of the average orbital radius is a constant value for all planets in the solar system.
How can we estimate the orbital period of a planet given its distance from the Sun?
-We can estimate the orbital period of a planet by using Kepler's third law. By knowing the average distance of the planet from the Sun (its orbital radius), we can apply the formula that relates the square of the period to the cube of the orbital radius, using the constant value for the solar system, to find the period in Earth years.
What is the significance of the conservation of mechanical energy in planetary orbits?
-The conservation of mechanical energy in planetary orbits implies that the total mechanical energy (the sum of kinetic and potential energy) remains constant throughout the orbit. This is because there are no external forces doing work on the system. When a planet is closest to the Sun (perihelion), it has the highest speed and lowest potential energy, and when it is farthest from the Sun (aphelion), it has the lowest speed and highest potential energy.
How does the shape of Mars's orbit around the Sun affect its orbital characteristics?
-The shape of Mars's orbit, like that of other planets, is an ellipse with the Sun at one focus. This elliptical shape, as described by Kepler's first law, affects Mars's speed and distance from the Sun throughout its orbit. Mars moves faster when it is closer to the Sun (perihelion) and slower when it is farther away (aphelion), as explained by Kepler's second law.
Outlines
📜 Introduction to Kepler's Laws of Planetary Motion
This paragraph introduces the topic of Kepler's laws of planetary motion, emphasizing their significance in describing the orbits of planetary objects around the Sun. It mentions the historical context of Johannes Kepler, a German mathematician and astronomer, and his contributions to the Scientific Revolution and Newton's Laws of universal gravitation. The paragraph outlines the objective of explaining Kepler's laws, which include the elliptical shape of planetary orbits with the Sun at one focus, the Law of Equal Areas which states that a planet sweeps out equal areas in equal times, and the conservation of angular momentum. It also sets the stage for a deeper exploration of these laws and their implications on planetary motion.
📐 Explanation of Kepler's Second and Third Laws
This paragraph delves into Kepler's second and third laws of planetary motion. The second law, also known as the Law of Equal Areas and Times, is explained through the concept of conservation of angular momentum, highlighting that the areas swept out by a planet in equal times are equal. The third law, which relates the periods of planets to their orbital radii, is simplified by considering circular orbits and using the relationship between speed, distance, and time. The mathematical formulation of the third law is explored, leading to the conclusion that planets closer to the Sun have shorter periods, and thus, years. The paragraph also provides examples to illustrate these laws, such as the highest speed of a planet at its closest point to the Sun and the longest revolution time for the farthest planet from the Sun.
🚀 Application of Kepler's Laws in Estimating Planetary Periods
The final paragraph applies Kepler's third law to estimate the orbital period of Mercury in terms of Earth years. It explains the process of using the given orbital radius and the constant ratio of periods to the cubes of orbital radii to calculate Mercury's period. The calculation involves converting the period from seconds to Earth years, considering the conversion factors for time. The result confirms that Mercury, being closer to the Sun, has a shorter period than Earth, aligning with the principles of Kepler's laws. The paragraph concludes by encouraging further exploration of Kepler's laws for a deeper understanding of planetary motion.
Mindmap
Keywords
💡Kepler's Laws of Planetary Motion
💡Ellipses
💡Conservation of Angular Momentum
💡Orbital Radius
💡Period of Orbit
💡Universal Gravitation
💡Johannes Kepler
💡Scientific Revolution
💡Gravitational Constant
💡Mechanical Energy
💡Gravitational Potential Energy
Highlights
Kepler's laws of planetary motion describe the orbits of planetary objects around the Sun.
Johan Kepler was a German mathematician and astronomer who contributed to the 17th century Scientific Revolution and laid groundwork for Newton's Laws of universal gravitation.
Kepler's first law states that the orbits of planetary bodies are ellipses, with the Sun as one of the foci.
Kepler's second law, also known as the Law of Equal Areas, states that a planet sweeps out equal areas in equal times.
The second law is related to the conservation of angular momentum, meaning the angular momentum of a system is constant when no external forces are present.
Kepler's third law establishes a relationship between the square of a planet's orbital period and the cube of its orbital radius.
The third law simplifies to a constant ratio of the squares of the periods to the cubes of the orbital radii for planets in the solar system.
Planets closer to the Sun have shorter periods and thus experience a shorter year compared to those farther away.
The highest speed of a planet in its elliptical orbit occurs when it is closest to the Sun, as per Kepler's laws.
Gravitational potential energy is greatest when a planet or satellite is farthest from the Sun, while kinetic energy is highest when closest.
The total mechanical energy remains constant at all points in a planet's orbit due to the conservation of energy and absence of external forces.
Mars's orbit around the Sun is accurately described as an ellipse, according to Kepler's first law.
Mercury, having a shorter orbital radius, has a period of less than one Earth year, in accordance with Kepler's third law.
Kepler's laws of planetary motion are fundamental to understanding the dynamics of celestial bodies and their interactions within the solar system.
The laws provide a framework for predicting and analyzing the motion of planets, which was revolutionary for astronomy and physics.
Kepler's work was instrumental in the development of modern astronomy and had a profound impact on the scientific understanding of our universe.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: