Calculus 1 Lecture 1.1: An Introduction to Limits
TLDRThis engaging calculus lesson introduces the concept of limits, which is foundational to understanding calculus. The instructor explains the importance of limits in finding the slope of a curve at a specific point and approximating the area under a curve. Through illustrative examples, the lesson demonstrates how to compute one-sided limits and highlights the significance of the function values approaching a certain number from both the left and right. The session also touches on the concept of asymptotes and how they relate to limits, providing a solid grasp of the basics of limits in calculus.
Takeaways
- 📚 The foundation of calculus is the concept of limits, which is essential for understanding the subject.
- 🎯 The primary goals of calculus are to find the slope (or tangent) of a curve at a point and to calculate the area under a curve between two points.
- 🚩 The tangent problem involves finding the slope of a curve at a specific point, which is crucial for understanding calculus.
- 🤔 The idea of a limit is to determine how close one point can get to another without them being the same point, which is fundamental in calculus.
- 📈 The process of finding the slope of a curve involves using the concept of a secant line, which approximates the tangent line as it gets closer to the point of interest.
- 🔢 The slope of a secant line is found using the formula (Y2 - Y1) / (X2 - X1), which helps in understanding the behavior of the curve.
- 🌐 The area problem in calculus is about finding the area under a curve, which can be approximated by breaking it down into infinitesimally small rectangles.
- 💡 The concept of limits is not about the function's value at a specific point but what happens as the variable approaches that value.
- 🛑 It's important to note that for a limit to exist at a point, the left-sided limit and the right-sided limit must be equal.
- 📊 The process of finding limits can be demonstrated graphically through the behavior of the function as it approaches certain values.
Q & A
What are the two primary goals of calculus as introduced in the lecture?
-The two primary goals of calculus discussed are: 1) finding the slope or tangent of a curve at a specific point, and 2) determining the area under a curve between two points. These concepts form the foundational objectives for understanding differential and integral calculus.
What is the significance of limits in calculus according to the transcript?
-Limits are fundamental to calculus as they help understand how functions behave as inputs approach a certain value. The concept of limits is crucial for defining derivatives and integrals, which are central to studying the changes and areas under curves, respectively.
How does the lecture describe finding the slope of a curve at a point?
-The lecture explains that finding the slope of a curve at a point involves using the concept of limits to make a secant line (which intersects the curve at two points) approximate a tangent line (which touches the curve at exactly one point) more closely by moving one point of the secant line closer to the point of interest.
Why can't we just let the point Q equal P when trying to find the tangent line at point P?
-If point Q were to equal P, it would mean we only have one point, not two distinct points needed to define a line. This would make it impossible to determine the slope at that point, as the concept requires a comparison between two distinct points on the function.
What does it mean when the transcript mentions moving point Q 'infinitesimally close' to point P?
-Moving point Q 'infinitesimally close' to P refers to the idea of making Q approach P as closely as possible without actually being the same point. This approach helps in approximating the slope of the tangent more accurately by limiting the difference between the secant and tangent lines.
What is the tangent problem introduced in the lecture?
-The tangent problem involves determining the equation of a tangent line to a curve at a specific point. This problem highlights the need to find the slope at that point using the concept of limits, as directly calculating the slope at a single point on a curve is not feasible with straightforward methods.
How does the concept of a secant line help in understanding calculus?
-A secant line, which intersects a curve at two points, serves as an initial approximation for a tangent line. By adjusting the position of one point of the secant closer to the target point, the slope of the secant line becomes a closer approximation to that of the tangent line, illustrating the limit process in calculus.
What is the 'area problem' in calculus as described in the transcript?
-The 'area problem' in calculus is about determining the area under a curve between two points. This is fundamentally challenging with basic geometry and requires calculus, specifically integral calculus, to solve by approximating the area using an infinite number of infinitesimally thin rectangles under the curve.
Why is it impossible to find the area under a curve using only pre-calculus methods according to the transcript?
-Pre-calculus methods are insufficient for finding the area under curves because they typically involve formulas applicable to simple geometric shapes like rectangles or triangles. Curves, however, require an understanding of limits and the ability to sum an infinite number of infinitesimal elements, which is beyond basic algebraic methods.
How does moving Q closer to P make the secant line a better approximation of the tangent line?
-Moving Q closer to P reduces the distance between the two points on the secant line, thus making the angle and slope of the secant line increasingly similar to those of the tangent line at P. This process leverages the concept of limits to ensure the secant line nearly replicates the tangent at the point of tangency.
Outlines
📚 Introduction to Calculus and Limits
The video begins with an introduction to calculus, emphasizing the importance of limits as the foundation of the subject. The instructor outlines the two primary goals of calculus: to find the slope of a curve at a specific point (the tangent) and to calculate the area under a curve between two points. The concept of a tangent line as a line that intersects a curve at a single point is introduced, and the idea of using calculus to determine this slope is discussed. The video sets the stage for a deeper exploration of calculus by highlighting the significance of limits in achieving these goals.
📈 Understanding the Tangent Problem
The second paragraph delves into the tangent problem, explaining the challenge of finding the slope of a curve at a given point. The instructor uses the analogy of a secant line, a line that connects two points on a curve, to illustrate the concept of approximation. The idea is to make the secant line as close as possible to the curve's tangent line by moving the second point, Q, closer to the first point, P. The instructor emphasizes that the secant line becomes a better approximation of the tangent line as point Q approaches point P, introducing the concept of a limit in calculus.
🔍 The Concept of Limits
This paragraph further explores the concept of limits, explaining how close one point can get to another without them being the same. The instructor clarifies that while two points are needed to define a line, the idea of a limit allows us to consider points that are 'infinitely close' to each other. The notion of a limit is used to describe the process of a quantity approaching a certain value but never actually reaching it. The instructor emphasizes that understanding limits is crucial for grasping the fundamentals of calculus.
🌟 Applying Limits to Find Tangent Slopes
The fourth paragraph demonstrates how to apply the concept of limits to find the slope of a tangent line at a specific point on a curve. The instructor guides the audience through the process of using a secant line and the slope formula to find the slope of the tangent. The example given involves a point on the curve and a secant line that approaches the point. By using limits to allow the point on the secant line to get infinitely close to the point on the curve, the instructor shows how to calculate the slope of the tangent line, which is the central goal in studying calculus.
📝 Working with Functions and Slopes
In this paragraph, the instructor continues the discussion on finding the slope of a tangent line by introducing the concept of functions and how they relate to the coordinates of points on a curve. The focus is on understanding the relationship between the x and y coordinates, particularly in the context of the slope formula. The instructor emphasizes the importance of keeping the variables in terms of one variable and uses the example of a function y = x^2 to illustrate how to find the slope of the tangent line at the point (1,1). The process involves factoring and simplifying expressions to find the slope, which is key to solving calculus problems.
🤔 Reflecting on the Limit Process
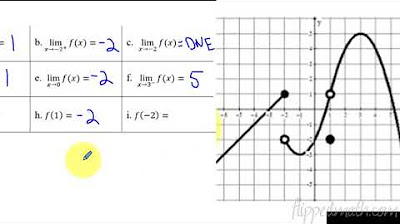
The instructor reflects on the process of finding limits and the significance of understanding what a function does as a variable approaches a certain value. The discussion includes the importance of not focusing on the function's value at the exact point but rather on the behavior as it gets closer to that point. The concept of one-sided limits is introduced, explaining that the function must approach the same value from both the left and the right for a limit to exist. The instructor emphasizes that the limit is about the function's behavior as it approaches a value, not the value itself.
📊 Visualizing Limits with Tables
The paragraph discusses the use of tables to visualize and understand limits. The instructor guides the audience through creating a table to find the limit of a function as x approaches a certain value. The table includes values of x approaching the point of interest from both the left and the right, along with the corresponding function values. The process involves observing the trend of the function values as they get closer to the point, which helps determine the limit. The instructor highlights the importance of symmetry in the approach from both sides to confirm the existence of a limit.
🤯 Understanding One-Sided Limits
The video continues with a deeper exploration of one-sided limits, explaining how to find the limit as x approaches a certain value from the right or from the left. The instructor clarifies the notation used for right-sided and left-sided limits and emphasizes that for a limit to exist at a point, the left-sided limit must equal the right-sided limit. The concept is illustrated by examining the behavior of the function values as they approach the point from both directions and comparing whether they meet at the same value.
🌐 Graphing and Analyzing Limits
The final paragraph of the video script discusses the application of limits in graphing functions, particularly focusing on what happens when the function approaches zero. The instructor explains the concept of positive and negative infinity in the context of limits and how they relate to asymptotes. The discussion includes the behavior of function values as they approach a certain point from the right or the left, and how these behaviors can be used to determine the existence of a limit. The instructor also introduces the idea of using limits to predict the behavior of a function near undefined points, providing a deeper understanding of the function's overall trend.
Mindmap
Keywords
💡Calculus
💡Limits
💡Tangent
💡Slope
💡Secant Line
💡Area Under a Curve
💡Rate of Change
💡Approximation
💡Instantaneous
💡Derivatives
Highlights
The introduction to calculus and its fundamental concept of limits.
Explaining how limits allow us to find the slope of a curve at a specific point.
The two main goals of calculus: finding the slope or tangent of a curve and calculating the area under a curve.
The concept of a secant line and how it approximates the tangent line.
The importance of understanding the difference between a secant and a tangent line.
The illustration of how moving a point on a curve closer to another point can approximate the tangent line.
The explanation of the limit concept and its role in calculus.
The process of finding the slope of a curve using the idea of a limit.
The introduction of the slope formula and its application to the secant line.
The concept of undefined expressions and how factoring can help in finding limits.
The method of simplifying expressions to better understand the slope of a secant line.
The idea of a limit as a function approaches a given value without necessarily reaching it.
The demonstration of how the limit can be used to find the equation of a tangent line.
The explanation of how calculus can be used to find the area under a curve between two points.
The concept of approaching a value from the right and left in the context of limits.
The importance of the function approaching the same value from both sides for the limit to exist.
The introduction of right-sided and left-sided limits and their significance in understanding the behavior of functions.
The explanation of how limits can involve infinity and the concept of asymptotes.
The method of using tables to discover limits and understand the behavior of functions as they approach certain values.
The discussion on the non-existence of limits in certain cases and how that affects the understanding of function behavior.
The practical application of limits in understanding the behavior of functions and their graphical representation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: