AP Calculus AB - 1.3 Estimating Limit Values From Graphs

Daniel Bortnick

4 Oct 202018:33

EducationalLearning

32 Likes 10 Comments

TLDRIn this AP Calculus AB Unit 1 video, Mr. Bortnick explores limits, continuity, and the concept of estimating limit values from graphs. He introduces notation, informal and formal definitions of limits, and the significance of one-sided limits. The instructor illustrates how to determine limits from the left and right, emphasizing the importance of direction in limit calculations. Through examples, he demonstrates how to interpret graphs to find limits and construct functions that satisfy given limit conditions, providing a comprehensive understanding of limits in calculus.

Takeaways

📚 The lesson is focused on estimating limit values from graphs, which is a key topic in the AP Calculus AB Unit 1.
📝 The notation for a limit statement is introduced as \( \lim_{x \to c} f(x) = l \), emphasizing that \( c \) and \( l \) are real numbers and the components should not be separated.
🔍 An informal definition of a limit is provided, stating that as \( x \) approaches \( c \) from both sides, the function values \( f(x) \) approach a value \( l \).
👉 The concept of one-sided limits is introduced, highlighting the direction from which \( x \) approaches \( c \), either from the left (negative direction) or from the right (positive direction).
🔢 The notation for one-sided limits is explained, with a '+' sign indicating approach from the right and a '-' sign indicating approach from the left.
📉 The formal definition of a limit is presented, stating that an overall limit exists if and only if the left and right limits are equal, otherwise the limit does not exist (DNE).
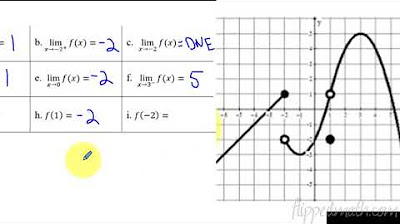
📈 The script provides examples of how to determine one-sided limits from a graph, illustrating how to read the y-values as \( x \) approaches a certain point from different directions.
📊 The importance of understanding whether a limit exists at a point is discussed, which relies on the equality of the left and right limits.
📐 A practical example is given to sketch a graph of a function that satisfies given conditions, including specific points, limit values, and the behavior of the function (increasing/decreasing).
📚 The lesson concludes with an invitation for students to practice estimating limits from graphs and to check their solutions against provided answers.
💬 The instructor encourages students to reach out with any questions, emphasizing the importance of understanding the concepts of limits and continuity.

Q & A

What is the topic of the lecture by Mr. Bortnick?
-The topic of the lecture is estimating limit values from graphs, which is part of the AP Calculus AB Unit 1.
What is the limit statement notation and what does it represent?
-The limit statement notation is 'lim (f(x) as x approaches c) = l', where c and l are real numbers. It represents the value that the function f(x) approaches as x gets arbitrarily close to c.
What is the informal definition of a limit?
-The informal definition of a limit states that as x gets really close to c from both sides, the y values of the function f(x) get really close to some value l.
What are one-sided limits and how are they notated?
-One-sided limits are limits that come from a certain direction, either from the left or the right. They are notated with a '+' sign for the right side (lim (f(x) as x approaches c+) = l) and a '-' sign for the left side (lim (f(x) as x approaches c-) = l).
What is the formal definition of a limit according to the script?
-The formal definition of a limit is that if the limit from the right side (lim (f(x) as x approaches c+) = l) and the limit from the left side (lim (f(x) as x approaches c-) = l) are equal to each other, then the overall limit (lim (f(x) as x approaches c) = l) exists and is equal to l.
What does it mean if the one-sided limits from the left and right are not equal?
-If the one-sided limits from the left and right are not equal, it means that the overall limit does not exist, which can be abbreviated as 'DNE' for 'does not exist'.
How can you determine the limit of a function as x approaches a certain value from the graph?
-You can determine the limit by observing the y-value that the function approaches as x gets closer to the given value from either the left or the right side.
What is the difference between the actual output of a function and the limit of the function at a certain point?
-The actual output of a function at a certain point is the y-value of the function when x equals that specific value. The limit of the function at that point is the y-value the function approaches as x gets arbitrarily close to that value.
How does the script illustrate the concept of a function increasing?
-The script illustrates the concept of a function increasing by stating that between two points, say from x = -2 to x = 3, the function's graph is going upwards, indicating that the function is increasing over that interval.
What is a piecewise function and how is it related to the script?
-A piecewise function is a function that is defined by different expressions over different intervals. The script relates to this by providing an example of sketching a graph of a function that satisfies multiple conditions, which could be represented as a piecewise function.

Outlines

00:00

📚 Introduction to Limits and Continuity

This paragraph introduces the topic of limits and continuity in the context of AP Calculus AB. The speaker, Mr. Bortnick, begins by discussing the notation and informal definition of limits, emphasizing the importance of keeping the function notation together. He explains limits as y-values that the function approaches as x gets close to a certain value, c, from both sides. The concept of one-sided limits is introduced, highlighting the difference between approaching a value from the left (negative direction) and from the right (positive direction), and how this is denoted in mathematical notation with a plus or minus sign next to the value c.

05:01

🔍 Formal Definition and Existence of Limits

The speaker proceeds to the formal definition of a limit, explaining that for an overall limit to exist, the one-sided limits from the left and right must be equal. If these one-sided limits differ, the overall limit does not exist, denoted by 'DNE' (does not exist). This paragraph also includes examples of how to interpret one-sided limits from a graph and how to write the corresponding limit statements, emphasizing the importance of recognizing when the function does not have a limit at a certain point.

10:01

📉 Analyzing Limits from Graphs

This section delves into the process of estimating limit values directly from graphs. The speaker provides step-by-step analysis of various points on a graph, demonstrating how to determine one-sided limits and the overall limit when applicable. The importance of recognizing when a function does not have a limit at a certain point is reiterated, with examples showing how to interpret the graph's behavior as x approaches specific values from both the left and right sides.

15:02

📈 Constructing a Function with Given Limit Conditions

The final paragraph focuses on constructing a function that satisfies a set of limit conditions. The speaker guides the audience through the process of sketching a function that meets specific criteria, such as passing through certain points, having defined limits as x approaches particular values, and exhibiting certain behaviors like being increasing over an interval. The process involves understanding the implications of the given conditions on the function's graph and connecting these points to form a coherent piecewise function that meets all the stipulated requirements.

Mindmap

Keywords

💡Limit

A 'limit' in calculus is a fundamental concept that describes the value that a function approaches as the input (x) approaches a particular value. It is central to the video's theme of understanding the behavior of functions. The script introduces the limit notation \( \lim_{x \to c} f(x) = l \), where 'c' is the value x approaches and 'l' is the limit value. The video discusses how limits can be estimated from graphs and the importance of one-sided limits, which are limits approached from the left or right.

💡Continuity

While not explicitly defined in the script, 'continuity' is a concept closely related to limits. A function is continuous at a point if the limit of the function as x approaches that point is equal to the function's value at that point. The script's focus on estimating limit values from graphs implies the importance of continuity in analyzing the behavior of functions.

💡One-sided Limit

A 'one-sided limit' refers to the value a function approaches as x gets arbitrarily close to a certain point from either the left or the right. The script distinguishes between limits approached from the right, denoted by \( \lim_{x \to c^+} \), and from the left, denoted by \( \lim_{x \to c^-} \). These are crucial for understanding the behavior of functions near points where the function may not be defined or where the function's value jumps.

💡Graph

A 'graph' in the context of the video represents the visual representation of a function's behavior, plotting the y-values (output) against the x-values (input). The script emphasizes estimating limit values from graphs, which is a practical way to visualize and understand the approach of a function's values towards a limit.

💡AP Calculus AB

AP Calculus AB is a college-level calculus course and exam offered by the College Board. The script is part of a series on this topic, indicating that the content is geared towards high school students preparing for the AP exam. The video specifically covers unit 1, which is focused on foundational concepts like limits and continuity.

💡Notation

In the context of the script, 'notation' refers to the specific symbols and expressions used to represent mathematical concepts, such as limits. The script explains the standard limit notation and the significance of keeping the function notation together when writing limit statements.

💡Formal Definition

The 'formal definition' of a limit in the script provides the precise mathematical criteria for when a limit exists. It states that if the one-sided limits from the left and right are equal, then the overall limit exists and is equal to that common value. This is contrasted with the informal definition, which is more conceptual.

💡Informal Definition

An 'informal definition' is a less rigorous explanation of a concept, used here to describe a limit as the value that the y-values of a function get close to as x gets close to a certain value from both sides. The script uses this to introduce the concept before presenting the formal definition.

💡Existence of a Limit

The 'existence of a limit' is determined by comparing the one-sided limits. If the limit from the left and the limit from the right are equal, the overall limit exists and is equal to that value. The script uses this concept to explain when a function has a limit at a particular point and when it does not.

💡DNE (Does Not Exist)

DNE stands for 'Does Not Exist' and is used in the script to denote situations where the overall limit of a function as x approaches a certain value does not exist because the one-sided limits are not equal. This is a key concept in understanding the limitations of limits and the behavior of functions at certain points.

💡Practice Problems

The script includes 'practice problems' as a way for students to apply their understanding of limits and one-sided limits by estimating limit values from given graphs. These problems are an integral part of the learning process, allowing students to see the concepts in action and to develop their problem-solving skills.

Highlights

Introduction to limits and the concept of estimating limit values from graphs.

Explanation of limit notation and its importance in mathematical expressions.

Informal definition of a limit in terms of the function's y-values approaching a specific value.

Introduction of one-sided limits and the significance of direction in limit evaluation.

Notation differences for limits coming from the right or left side.

Formal definition of a limit requiring equality of left and right limits.

Use of 'dne' to denote that a limit does not exist.

Graphical representation of one-sided limits and how to interpret them.

Examples of determining one-sided limits from a graph.

Conditions for the existence of an overall limit based on left and right limits.

Graphical method to determine if a function is increasing or decreasing.

How to sketch a graph of a function that satisfies given limit conditions.

Process of verifying if a sketched graph meets all the specified limit conditions.

Explanation of how to handle discontinuities and undefined points on a graph.

Importance of understanding the direction of limits in function analysis.

Practical application of limit concepts in solving calculus problems.

Encouragement for students to practice limit problems for better understanding.

Offer of solutions and support for students to check their work and ask questions.

Transcripts

Browse More Related Video

AP Calculus AB - 1.5 Determining Limits Using Algebraic Properties of Limits

Calculus AB/BC – 1.3 Estimating Limit Values from Graphs

AP Calculus AB - 1.9 Connecting Multiple Representations of Limits

How To Tell If The Limit Exists

AP Calculus AB - 1.4 Estimating Limit Values from Tables

One-sided limits from tables | Limits and continuity | AP Calculus AB | Khan Academy