Equations of motion - Kinematics in one dimension - acceleration, velocity (initial, final) -Physics
TLDRThe video script is an engaging and informative lecture on the fundamentals of physics, specifically focusing on the equations of motion and kinematics in one dimension. The speaker, Meosis Perfectional, breaks down complex concepts into simpler terms, using analogies and clear explanations to illustrate key principles such as velocity, acceleration, displacement, and their interrelations. The lecture progresses systematically, introducing each equation and its corresponding graphical representation, and then applying them to solve practical problems. The speaker encourages active participation, prompting viewers to solve problems along the way and providing detailed walkthroughs of the solutions. The content is both educational and entertaining, making it an excellent resource for anyone looking to understand or review the basics of physics motion.
Takeaways
- 📚 The basics of physics kinematics, specifically motion in one dimension, are discussed in the video.
- 🌟 The first equation introduced is displacement (D) equals velocity (V) times time (T), or D = VT.
- 📈 The relationship between displacement and time can be graphed, with the slope representing velocity.
- 🔄 The second equation derived is the change in displacement over change in time equals velocity, leading to the final position equation: final position = initial position + V*T.
- 🚀 The concept of acceleration is introduced as the change in velocity over change in time, with the second equation relating to acceleration being final velocity equals initial velocity plus acceleration times time (Vf = Vi + a*T).
- 📊 The third key equation relates displacement to time and acceleration, showing displacement equals initial velocity times time plus half of acceleration times time squared (D = Vi*T + 0.5*a*T^2).
- 📈 The video emphasizes the direct proportionality between velocity and time when acceleration is constant, and graphically represents this as a straight line on a graph.
- 🤔 The average velocity is defined as the total displacement over total time, and can be calculated as the average of the initial and final velocities.
- 🔢 A fourth equation is presented relating velocity, displacement, and acceleration: displacement equals final velocity squared minus initial velocity squared divided by 2 times acceleration (D = (Vf^2 - Vi^2) / 2a).
- 🚗 The script includes practical examples and problems involving a car's motion, deceleration, and uniform acceleration to illustrate the application of the equations.
- 📝 The importance of understanding and applying these kinematic equations for problem-solving in physics is highlighted throughout the video.
Q & A
What is the first equation of motion discussed in the video?
-The first equation of motion discussed is D = VT, where D represents displacement, V is velocity, and T is time.
How can the relationship between displacement and time be graphed?
-The relationship between displacement and time can be graphed with the change in displacement in meters on the Y-axis and the change in time in seconds on the X-axis. The slope of the line represents velocity.
What is the second equation of motion derived in the video?
-The second equation of motion derived is V = VI + a*T, where V is the final velocity, VI is the initial velocity, a is acceleration, and T is time.
How is acceleration defined in the context of motion?
-Acceleration is defined as the change in velocity over the change in time, represented by the equation a = (Vf - Vi) / T, where Vf is the final velocity, Vi is the initial velocity, and T is the time interval.
What does the video explain about the direct proportionality between two entities?
-The video explains that if two entities are divisible by one another or subtractable from one another, their relationship is directly proportional. For example, if acceleration (a) remains constant, velocity (V) is directly proportional to time (T).
How does the video describe the concept of average velocity?
-The video describes average velocity as the total displacement divided by the total time, represented by the equation V_avg = (Vf + Vi) / 2, where Vf is the final velocity and Vi is the initial velocity.
What is the third equation of motion presented in the video?
-The third equation of motion presented is D = Vi*T + 0.5*a*T^2, where D is displacement, Vi is the initial velocity, T is time, and a is acceleration.
How can the relationship between displacement and time when starting from rest be represented graphically?
-When starting from rest, the relationship between displacement and time can be represented graphically as a straight line with a slope equal to half of the acceleration (a/2), since the initial velocity is zero.
What is the significance of the equation 2ad = Vf^2 - Vi^2?
-The equation 2ad = Vf^2 - Vi^2 is significant because it relates displacement, initial and final velocities, and acceleration, allowing us to solve for one of these variables if the others are known.
How does the video explain the concept of uniform acceleration?
-The video explains uniform acceleration as a constant rate of change of velocity, meaning the acceleration does not change over time. This results in a straight line graph when velocity is plotted against time.
What is the practical example given in the video to illustrate the equations of motion?
-The practical example given in the video is an airplane landing on a runway at a certain velocity and decelerating uniformly until it stops. The example is used to illustrate how to use the equations of motion to calculate the time it takes for the airplane to come to a stop.
Outlines
📘 Introduction to Equations of Motion
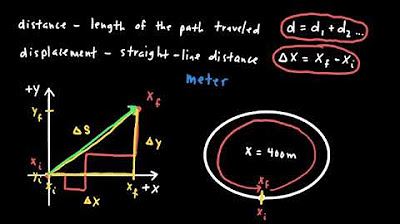
The video begins with an introduction to the equations of motion in one dimension, specifically focusing on kinematics. The speaker, Meosis, welcomes viewers back to the physics playlist and provides a brief recap of previous topics covered. Today's focus is on relating displacement, velocity, time, and acceleration through various equations. The first equation discussed is the basic formula for speed, which is distance over time, and then velocity, which is displacement over time. The speaker emphasizes the importance of understanding each equation and its corresponding graph, setting the stage for a deep dive into the physics of motion.
📊 Graphing Velocity and Displacement
This paragraph delves into the graphical representation of the relationship between velocity and displacement over time. The speaker explains how to graph the equation for velocity, emphasizing the significance of the Y-axis (change in displacement in meters) and the X-axis (change in time in seconds). The concept of velocity as the slope of the line (ΔD/ΔT) is clarified. The speaker then introduces another equation for velocity in terms of change in displacement over change in time. The explanation includes a discussion on the relationship between initial and final positions and how to derive the equation for velocity in this context.
🚀 Understanding Acceleration
The speaker moves on to explain the concept of acceleration, which is the rate of change of velocity over time. The relationship between speed, displacement, velocity, and acceleration is explored, with a focus on how acceleration is calculated as the change in velocity over time. The speaker also introduces the equation for final velocity in terms of initial velocity, acceleration, and time. The graphical representation of this relationship is discussed, with the slope of the line representing acceleration. The concept of direct proportionality between velocity and time, given a constant acceleration, is also introduced.
📈 Deriving Equations from Basic Principles
In this section, the speaker derives further equations from fundamental principles. The process of elimination and rearrangement of terms to isolate variables is explained, leading to the development of equations that describe the motion of an object. The speaker emphasizes the importance of understanding the derivation process to gain a deeper understanding of the physics involved. The concept of average velocity is introduced, along with its equation and graphical representation. The relationship between average velocity, total displacement, and total time is clarified.
🔢 Solving for Displacement and Time
The speaker continues to explore the equations of motion, focusing on solving for displacement and time. The equations relating displacement to time and velocity to displacement are discussed, with the speaker demonstrating how to manipulate these equations to solve for the unknown variable. The concept of directly proportional relationships is revisited, with the speaker explaining how displacement is directly proportional to time when velocity is constant. The graphical representation of this relationship is also covered, with the slope of the line representing the constant acceleration.
📚 Applying Equations to Real-World Scenarios
The speaker applies the learned equations to real-world scenarios, such as an airplane decelerating to a stop and a car moving with uniform velocity. The process of converting units and using the equations to find unknown quantities is demonstrated. The speaker also introduces a method for determining the initial velocity and acceleration of an object based on its displacement over time. The importance of understanding the direction of acceleration (positive or negative) is emphasized, as well as the ability to simplify equations based on the given conditions of a problem.
🎯 Graphical Analysis of Motion
This paragraph focuses on the graphical analysis of motion, with the speaker examining different graphs that represent the motion of an object under various conditions. The speaker explains how to interpret the slope of the lines in these graphs to determine acceleration and other physical quantities. The concept of uniform versus nonuniform acceleration is discussed, as well as the implications of starting from rest or a nonzero initial velocity. The speaker also provides guidance on how to identify the correct graph that represents a specific type of motion, such as uniform acceleration from rest.
📝 Solving Problems with Kinematic Equations
The speaker presents a series of problems that involve using the kinematic equations to find unknown quantities such as the final velocity, displacement, and time of motion. The problems involve different scenarios like a car stopping from a certain initial velocity and a car passing a traffic sign while decelerating. The speaker demonstrates how to apply the equations and unit conversions to solve these problems, emphasizing the importance of understanding the physical situation and selecting the appropriate equation to use. The speaker also provides answers to the problems and encourages viewers to practice solving similar problems to gain proficiency.
🎓 Summary of Kinematic Equations
In the concluding paragraph, the speaker summarizes the three main kinematic equations covered in the video: the relationship between displacement and time, the equation for final velocity in terms of initial velocity and acceleration, and the equation relating displacement, initial velocity, and acceleration. The speaker also provides a brief overview of the key concepts discussed, such as the importance of understanding the graphical representation of these equations and the direct proportionality between certain physical quantities. The speaker encourages viewers to review the equations and practice problem-solving to reinforce their understanding of the material.
📚 Additional Resources and Encouragement
The speaker concludes the video by providing information on where to find additional resources for learning physics, including notes on various topics and premium video courses. The speaker also encourages viewers to support the channel through various means and to subscribe for more content. A final word of encouragement is given, reminding viewers to stay safe, happy, and to study hard in their pursuit of understanding physics.
Mindmap
Keywords
💡Physics
💡Kinematics
💡Displacement
💡Velocity
💡Acceleration
💡Equations of Motion
💡Graphs
💡Deceleration
💡Uniform Motion
💡Direct Proportionality
💡Inverse Proportionality
Highlights
Introduction to the physics playlist and the topic of equations of motion in one dimension.
Explanation of the first equation, displacement equals velocity times time (D = VT).
Graphing the first equation to understand the relationship between velocity and time.
Derivation of the second equation from the concept of acceleration as the change in velocity over time.
Explanation of how to graph acceleration over time and its implications.
Introduction to the concept of directly proportional relationships using the example of velocity and time.
Derivation and simplification of the equation for displacement in terms of initial velocity, acceleration, and time.
Explanation of the relationship between average velocity, total displacement, and total time.
Derivation of the final equation for displacement in terms of velocity and acceleration.
Application of the equations of motion to solve real-world physics problems, such as an airplane decelerating to a stop.
Use of the equations to determine the initial velocity and acceleration of an object given its motion.
Explanation of uniform acceleration and how to identify it in graphical representations.
Solution to a problem involving a car decelerating to a stop and finding the displacement.
Discussion on the difference between positive and negative acceleration and its impact on motion.
Identification of the correct graph representing the motion of an object with uniform acceleration from rest.
Explanation of how to find the slope in various graphs and what it represents in terms of physical quantities.
Real-world application problem involving a car approaching a traffic light and the calculation of whether it will stop in time.
Summary of the key equations learned in the video and their practical applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: