The Metric System - Basic Introduction
TLDRThe video script discusses the metric system's prefixes and their corresponding multipliers, explaining how to convert between units. It covers prefixes from deca (10^1) to yocto (10^-24), and from deci (10^-1) to pico (10^-12), highlighting their symbols and multipliers. The script also provides a detailed methodology for unit conversion, using examples to illustrate how to convert quantities like meters to kilometers and liters to milliliters. It emphasizes the importance of understanding conversion factors and demonstrates how to perform both one-step and two-step conversions, ultimately enhancing the viewer's ability to handle metric system calculations effectively.
Takeaways
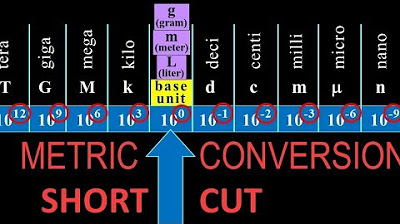
- 📐 The metric system prefixes are based on powers of 10, with deca (10^1), hecto (10^2), kilo (10^3), mega (10^6), giga (10^9), tera (10^12), and higher orders like peta (10^15), exa (10^18), zeta (10^21), and yotta (10^24).
- 🔄 Conversion within the metric system involves attaching the prefix multiplier to the base unit, such as 'deca' meaning 10 times the unit (e.g., 1 decameter = 10 meters).
- 📈 The script introduces both positive and negative exponents, where positive indicates larger units (like mega for million) and negative indicates smaller units (like deci for tenth).
- 🔢 For negative prefixes, such as deci (10^-1), centi (10^-2), and milli (10^-3), the conversion factors involve moving the decimal point to the left to reduce the size of the unit.
- 🌟 The script emphasizes the importance of understanding conversion factors, as they are crucial for solving problems that involve changing from one unit to another within the metric system.
- 🔄 When converting units, the process often involves simplifying the equation by canceling out unwanted units and leaving the desired unit.
- 📊 The script provides examples of one-step and two-step conversions, demonstrating how to manipulate the conversion factors to achieve the desired outcome.
- 🧠 Mental math can be used for unit conversions by understanding how moving negative exponents to the top of a fraction changes their sign and allows for addition with positive exponents.
- 🔍 The script encourages viewers to practice unit conversion by attempting examples on their own and referring to additional resources for more complex problems.
- 👨🏫 The information provided is valuable for educational purposes, particularly for those studying science or fields where understanding of the metric system is essential.
- 📚 The script serves as a comprehensive guide to understanding the metric system's prefixes, their symbols, and how to effectively use them for unit conversion.
Q & A
What is the prefix 'deca' and its corresponding symbol and multiplier in the metric system?
-The prefix 'deca' refers to a factor of 10 to the 1, or simply 10. Its symbol is 'd'.
What does the prefix 'hecto' represent in the metric system, and what are its symbol and multiplier?
-The prefix 'hecto' represents a factor of 10 squared, or 100. Its symbol is 'h', and the multiplier is 10 to the 2, which is 100.
What is the symbol and multiplier for the prefix 'kilo' in the metric system?
-The prefix 'kilo' has the symbol 'k' and represents a multiplier of 10 to the 3, or 1000.
How is the prefix 'mega' written, and what does it represent?
-The prefix 'mega' is written with a capital 'M' and represents a factor of 10 to the 6, or 1,000,000.
What is the prefix 'giga', and what does it stand for in terms of multiplication?
-The prefix 'giga' is represented by the capital letter 'G' and stands for a multiplication factor of 10 to the 9, which is equivalent to 1,000,000,000.
What is the conversion factor for converting centimeters to meters, and how is it derived?
-The conversion factor for centimeters to meters is 1 centimeter equals 10 to the negative 2 meters, derived from the prefix 'centi' meaning 10 to the minus 2.
How can you convert liters to milliliters using the conversion factor?
-To convert liters to milliliters, you use the conversion factor where 1 milliliter equals 10 to the negative 3 liters. You multiply the given liters by 10 to the 3 to get milliliters.
What is the process for converting a two-step unit like picometers to micrometers?
-To convert picometers to micrometers, first convert picometers to meters using the conversion factor (1 picometer = 10 to the negative 12 meters), then convert the resulting meters to micrometers using the conversion factor (1 micrometer = 10 to the negative 6 meters).
How do you mentally convert a large number of nanometers to kilometers?
-To mentally convert nanometers to kilometers, first convert nanometers to meters (1 nanometer = 10 to the negative 9 meters), then convert the resulting meters to kilometers (1 kilometer = 10 to the 3 meters). Adjust the decimal place accordingly to express the result in scientific notation.
What is the significance of the conversion factors in the metric system?
-Conversion factors are crucial for converting between different units within the metric system. They simplify the process by allowing you to attach a 1 to the prefix and then multiply by the base unit to convert from one unit to another.
What are the steps to perform a one-step conversion from meters to kilometers?
-To convert meters to kilometers, you start with the given number of meters, write the conversion factor (1 kilometer = 10 to the 3 meters), and then set up a fraction to cancel out the meters, leaving you with the result in kilometers.
What are the negative exponent prefixes in the metric system and their order?
-The negative exponent prefixes in the metric system, in order from smallest to largest, are: yocto (10 to the negative 24), zepto (10 to the negative 21), atto (10 to the negative 18), femto (10 to the negative 15), pico (10 to the negative 12), nano (10 to the negative 9), micro (10 to the negative 6), and milli (10 to the negative 3).
Outlines
📏 Introduction to Metric System Prefixes
This paragraph introduces the metric system prefixes and their corresponding symbols and multipliers. It begins with the deca prefix (symbol 'd', multiplier 10^1) and hecto ('h', 10^2), followed by kilo ('k', 10^3), mega ('M', 10^6), and giga ('G', 10^9). The explanation includes how to use these prefixes with base units, such as grams for mass, watts for power, and joules for energy. The paragraph also introduces the concept of conversion factors for problem-solving and emphasizes attaching the multiplier to the base unit for ease of use.
🔄 Writing Conversion Factors and Negative Exponents
This section delves into writing conversion factors using the metric system prefixes and understanding the significance of negative exponents. It explains how to convert standard units to smaller ones, such as centimeters to meters, milliliters to liters, and vice versa. The paragraph also covers prefixes like micro ('µ', 10^-6), nano ('n', 10^-9), and pico ('p', 10^-12), and their application in conversion factors. Additionally, it provides a method for adjusting equations to find common conversion factors and explains the process of converting units with a step-by-step example.
🔄 Converting Units: One-Step and Two-Step Processes
This paragraph discusses the methods for converting units within the metric system, both in one-step and two-step processes. It provides a clear explanation of how to convert larger units to smaller ones, such as meters to kilometers, and smaller units to larger ones, like liters to milliliters. The paragraph also introduces a two-step conversion example, where units like picometers are converted to meters and then to micrometers. The explanation includes the use of conversion factors and the importance of canceling out unwanted units to arrive at the desired unit.
🤔 Mental Math and Scientific Notation
The final paragraph focuses on mental math techniques and the use of scientific notation for unit conversion, particularly for more complex problems involving large or small numbers. It explains how to move negative exponents from the bottom to the top of a fraction and change their signs, allowing for the addition of exponents when multiplying common bases. The paragraph provides a detailed example of converting nanometers to kilometers, emphasizing the use of scientific notation for clarity and precision in the final answer. It also encourages viewers to practice these techniques and seek out additional resources for further learning.
Mindmap
Keywords
💡Metric System
💡Prefixes
💡Multipliers
💡Conversion Factors
💡Base Units
💡Positive and Negative Exponents
💡Scientific Notation
💡Unit Conversion
💡Decimal Places
💡Powers of Ten
💡Common Conversions
Highlights
Discussion of metric system prefixes and their corresponding symbols and multipliers begins with 'deca', which multiplies by 10.
The symbol for 'hecto' is lowercase 'h', and it multiplies by 10 squared or 100.
The prefix 'kilo' is symbolized by lowercase 'k' and represents multiplication by 10 to the third power or 1000.
One kilogram is a thousand grams, illustrating the relationship between kilo and grams.
The prefix 'mega' is denoted by a capital 'M' and signifies multiplication by 10 to the sixth power or a million.
A megawatt power plant produces energy equivalent to 1 times 10 to the sixth power watts or a million watts.
The prefix 'giga' is symbolized by a capital 'G' and stands for multiplication by 10 to the ninth power or a billion.
A giga joule is 1 times 10 to the ninth power joules, emphasizing the scale of the giga prefix.
Conversion factors are essential for solving problems and should always attach a '1' to the prefix, with the multiplier following the base unit.
The prefix 'tera' is symbolized by a capital 'T' and represents multiplication by 10 to the twelfth power or a trillion.
The prefix 'peta' is beyond the usual scope of most exams, with 'tera' typically being the limit.
Beyond 'tera', the prefix 'exa' is symbolized by a capital 'E' and stands for multiplication by 10 to the eighteenth power or a quintillion.
The prefix 'yotta' is symbolized by a capital 'Y' and represents multiplication by 10 to the twenty-fourth power or a septillion.
Negative exponent prefixes include 'deci', 'centi', and 'milli', with 'deci' being 10 to the minus one.
The prefix 'micro' is symbolized by a lowercase 'μ' and stands for multiplication by 10 to the minus six.
The process of converting units involves writing conversion factors and using them to cancel out the original unit and obtain the desired unit.
A step-by-step example of converting 478 meters to kilometers is provided, demonstrating the use of conversion factors.
A two-step conversion example is given, converting 496 picometers to micrometers, showcasing the method of converting between multiple units.
The transcript emphasizes the importance of understanding metric system prefixes and conversion factors for problem-solving.
Transcripts
Browse More Related Video
metric unit conversions shortcut: fast, easy how-to with examples

Converting Units With Conversion Factors - Metric System Review & Dimensional Analysis

Converting units of measurement with scientific notation (3 examples)

College Physics 1: Lecture 4 - Units and Unit Conversions

How to Convert Units in Chemistry

Shortcut for Metric Unit Conversion
5.0 / 5 (0 votes)
Thanks for rating: