Second Derivative Test
TLDRThe video script explains the second derivative test, a method to determine if a function has a maximum or minimum at a critical point. It demonstrates the process using an example function, showing how to find critical points, calculate the first and second derivatives, and apply the test to identify relative extrema. The script also covers an application of the test to a composite function G.
Takeaways
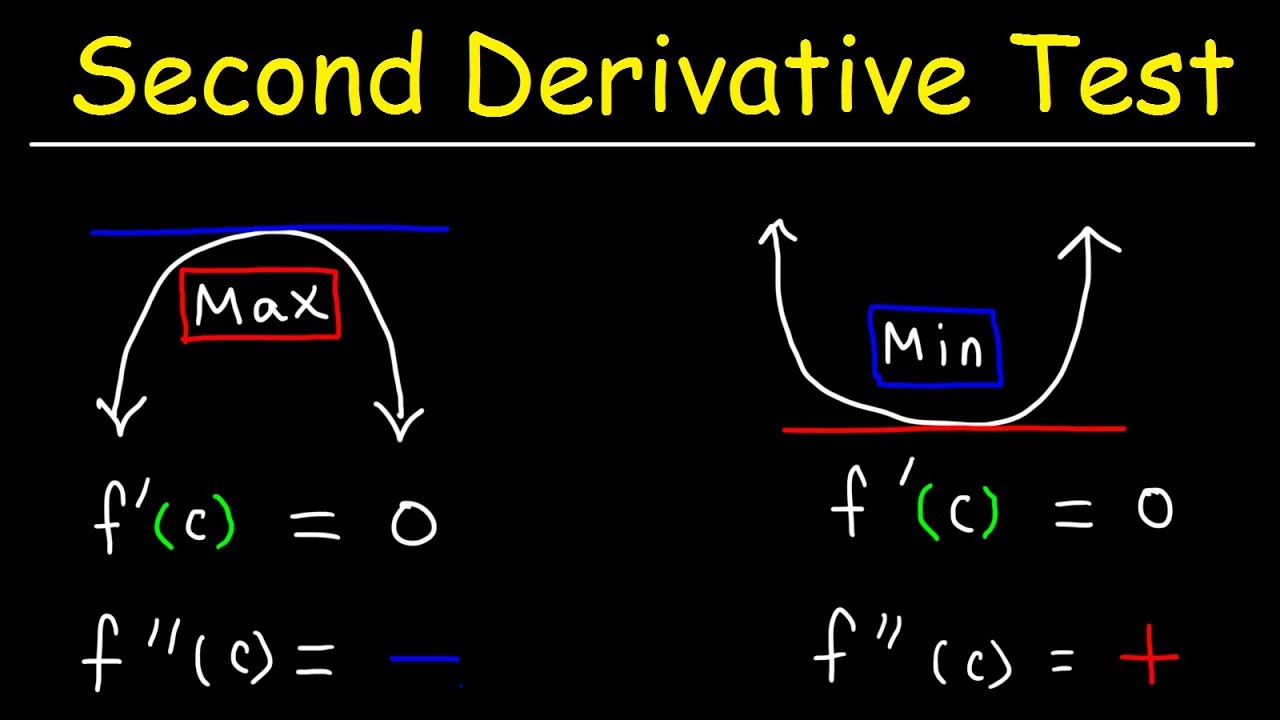
- 📘 The second derivative test is used to determine if a function has a maximum or minimum at a critical point where the first derivative is zero.
- 📚 If the second derivative (f'') is greater than zero at a critical point, the function has a relative minimum at that point.
- 📚 If the second derivative (f'') is less than zero at a critical point, the function has a relative maximum at that point.
- 🔍 To apply the second derivative test, first find the first derivative of the function and set it equal to zero to find critical points.
- 🔍 After finding critical points, calculate the second derivative of the function.
- 📊 The test involves substituting the critical points into the second derivative to determine if the function is concave up (minimum) or concave down (maximum).
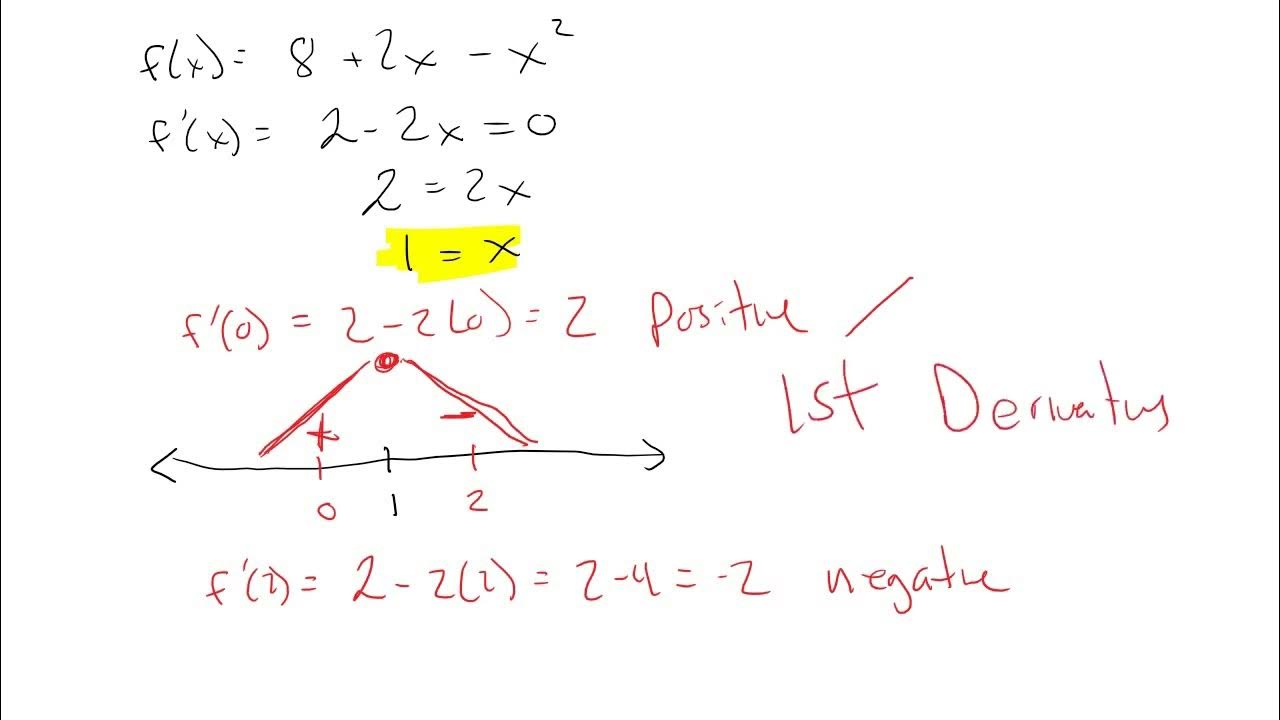
- 🔢 For the example given, the function's first derivative is factored to find critical points at x = 0 and x = ±1.
- 📈 The second derivative of the example function is calculated and used to determine that x = 1 is a relative maximum and x = -1 is a relative minimum.
- 📚 Another example involves a composite function G, which is defined in terms of another function f and its derivatives.
- 🔍 For G, the first derivative is set to zero to find critical points, and the second derivative is used to determine if G has a local maximum or minimum at x = 3.
- 📈 The calculation shows that G has a relative maximum at x = 3 because its second derivative is negative at this point.
Q & A
What is the second derivative test used for?
-The second derivative test is used to determine whether a critical point of a function is a relative minimum or maximum. It involves finding the second derivative of the function and evaluating its sign at the critical points.
What does it mean if the second derivative is greater than zero at a critical point?
-If the second derivative is greater than zero at a critical point, it indicates that the function is concave up at that point, which typically corresponds to a relative minimum.
What does it mean if the second derivative is less than zero at a critical point?
-If the second derivative is less than zero at a critical point, it indicates that the function is concave down at that point, which typically corresponds to a relative maximum.
How do you find the critical points of a function?
-To find the critical points of a function, you first take the first derivative of the function and set it equal to zero or where it does not exist. Solving these equations will give you the critical points.
What is the first step in applying the second derivative test?
-The first step in applying the second derivative test is to find the first derivative of the function and set it equal to zero to identify the critical points.
What happens if the second derivative at a critical point is zero?
-If the second derivative at a critical point is zero, the test is inconclusive, and you would need to use other methods, such as the first derivative test, to determine the nature of the critical point.
What is the function given in the script for the first example?
-The function given in the script for the first example is not explicitly stated, but it is implied to be a function whose first derivative involves a term that can be factored to \(x^2 - 1\).
What are the critical points found in the first example?
-In the first example, the critical points are found to be at \(x = 0\) and \(x = \pm 1\).
How does the script determine the nature of the critical points in the first example?
-The script determines the nature of the critical points by evaluating the second derivative at these points. A positive second derivative indicates a relative minimum, and a negative second derivative indicates a relative maximum.
What is the function G in the second example, and how is it related to the function F?
-The function G in the second example is defined as \(G(x) = x^2 - 9 \times 2f(x) + 5f'(x)\), where \(f(x)\) and \(f'(x)\) are given functions and their derivatives, respectively.
What is the conclusion about the function G at \(x = 3\) in the second example?
-In the second example, it is concluded that G has a relative maximum at \(x = 3\) because \(G'(3) = 0\) and \(G''(3) < 0\).
Outlines
📚 Introduction to the Second Derivative Test
The script introduces the second derivative test, a method used to determine whether a critical point on the graph of a function represents a relative maximum or minimum. It explains that if the first derivative (f') is zero and the second derivative (f'') is positive, the function is concave up, indicating a relative minimum. Conversely, if f'' is negative at a critical point, the function is concave down, indicating a relative maximum. The explanation is supported by an example where the first and second derivatives of a function are calculated to find the critical points and apply the second derivative test to determine the nature of these points.
🔍 Applying the Second Derivative Test with an Example
This paragraph delves into the application of the second derivative test using a specific function. The process involves taking the first derivative, setting it to zero to find critical points, and then calculating the second derivative. The critical points are tested by plugging them into the second derivative: a positive result indicates a relative minimum, while a negative result indicates a relative maximum. The example provided finds a relative maximum at x=1 and a relative minimum at x=-1 based on the second derivative test. Additionally, the paragraph explores a composite function G, which is defined in terms of another function f and its derivatives, and applies the second derivative test to determine whether G has a local maximum or minimum at x=3.
Mindmap
Keywords
💡Second Derivative Test
💡Critical Point
💡Concave Up
💡Concave Down
💡Derivative
💡Relative Minimum
💡Relative Maximum
💡Factoring
💡Product Rule
💡Composite Function
💡First Derivative Test
Highlights
Introduction to the second derivative test for determining relative maxima and minima.
Explanation of critical points and their significance in the second derivative test.
Condition for a relative minimum when the second derivative is greater than zero.
Condition for a relative maximum when the second derivative is less than zero.
Demonstration of finding critical points by setting the first derivative equal to zero.
Determination of critical points at x equals 0 and plus or minus 1.
Calculation of the second derivative and its role in the second derivative test.
Application of the second derivative test to determine a relative minimum at x equals negative one.
Application of the second derivative test to determine a relative maximum at x equals one.
Introduction of a function G and its relation to F and F prime.
Condition for a local maximum in function G based on G prime and G double prime.
Condition for a local minimum in function G based on G prime and G double prime.
Calculation of G prime at x equals 3 and its result being zero.
Determination that x equals 3 is a critical point for G.
Calculation of G double prime and its components.
Application of the second derivative test to function G at x equals 3.
Conclusion that G has a relative maximum at x equals 3 based on the second derivative test.
Transcripts
Browse More Related Video

Second derivative test | Using derivatives to analyze functions | AP Calculus AB | Khan Academy

Fiding Relative Max, Min and Inflection Point with Derivatives F4
Second Derivative Test

Calculus 1: Relative Extrema Examples
The First Derivative Test

Use the Second Derivative Test to Find Any Extrema and Saddle Points: f(x,y) = -4x^2 + 8y^2 - 3
5.0 / 5 (0 votes)
Thanks for rating: