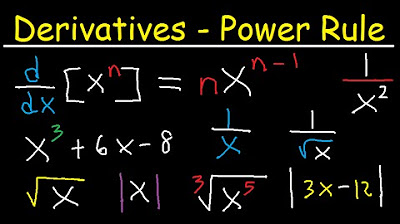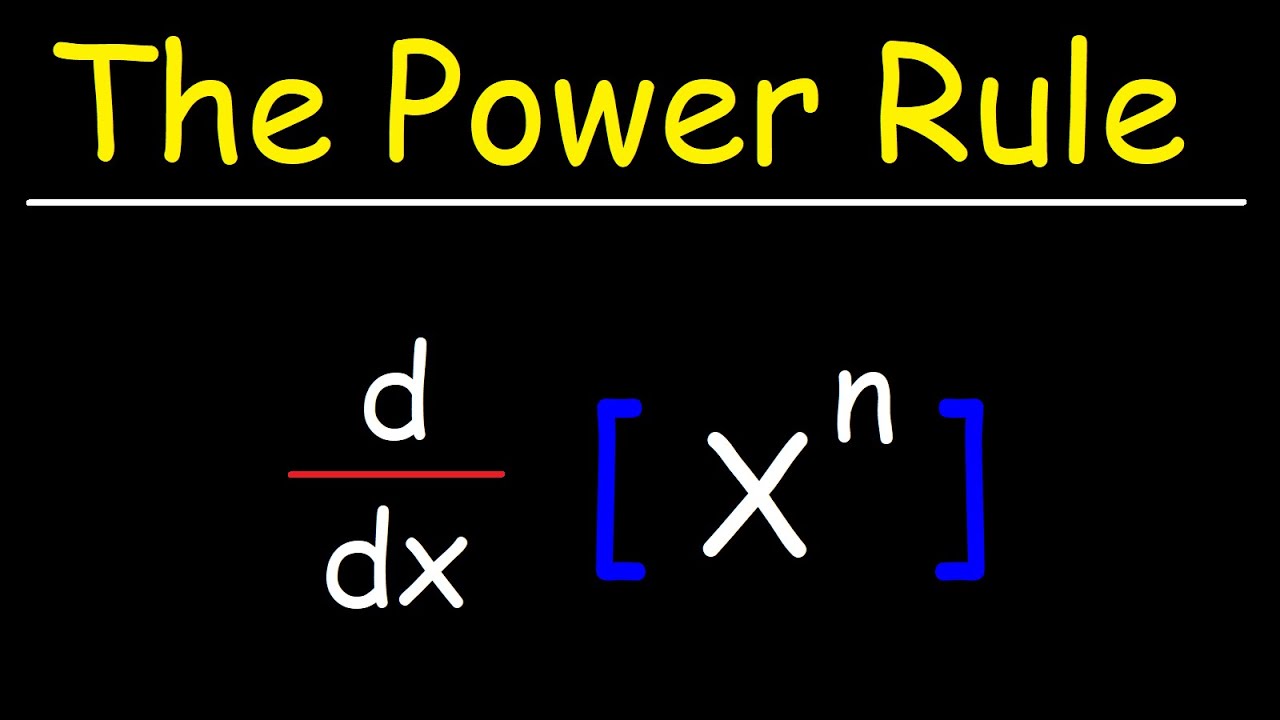Derivatives of Radical Functions

The Organic Chemistry Tutor
26 Feb 201815:30
EducationalLearning
32 Likes 10 Comments

TLDRThis transcript offers a comprehensive guide on deriving the derivatives of radical functions. It begins with simplifying radical expressions into rational exponents and applying the power rule. The video explains the use of the chain rule for composite functions and demonstrates multiple examples, including derivatives of square and cube roots, as well as rationalizing denominators in the final answers. The process is methodical, emphasizing the importance of understanding the underlying mathematical principles to solve such problems effectively.

Takeaways
  • 📝 The process of finding the derivative of radical functions involves rewriting the radical expression as a rational exponent.
  • 📌 To differentiate the square root of x, apply the power rule by rewriting the square root as x to the power of 1/2 and then use the rule to find the derivative, which results in (1/2)x^(-1/2) or 1/(2√x).
  • 🔄 When dealing with radical functions, the chain rule is often used in conjunction with the power rule to handle composite functions.
  • 🌟 For the square root of (x + 5), the derivative is found by differentiating using the power rule and chain rule, resulting in (1/2)√(x + 5).
  • 📈 For more complex expressions like the square root of (x^2 - 4), the chain rule is applied to find the derivative, which simplifies to x/√(x^2 - 4).
  • 👉 The cube root of (5x + 2) is differentiated by rewriting the expression with rational exponents and applying the chain rule, leading to the result of 5(√(5x + 2))/[3(5x + 2)^2] after rationalizing the denominator.
  • 📝 When rationalizing the denominator, multiply both the numerator and the denominator by the conjugate of the denominator to eliminate the radical from the denominator.
  • 🔢 For the expression 1/(√(x^5)), the derivative is found by first rewriting the expression and then applying the power rule, resulting in the final answer of -(5/4)√(x^9).
  • 🔧 The constant multiple rule is used when differentiating constants multiplied by expressions, which is evident in the example of 8/(√(3 - 2x)^4), where the derivative is -64/(7√(3 - 2x)^3).
  • 📊 The script emphasizes the importance of simplifying and converting back to radical form after finding the derivative of radical functions for clarity and standardization.
  • 📚 Practice is key to mastering the process of differentiating radical functions, as suggested by working through various examples provided in the script.
Q & A

  • What is the process for finding the derivative of the square root of x?

    -To find the derivative of the square root of x, first rewrite the square root as a rational exponent (x to the power of 1/2). Then apply the power rule, which involves moving the exponent to the front and subtracting 1 from the exponent. The result is 1/2 multiplied by x to the power of -1/2. Simplify the expression by taking the variable to the bottom and converting the negative exponent back to a positive one. Finally, convert the rational exponent back to its radical form, which gives the derivative as the square root of x divided by 2.

  • How do you use the chain rule to find the derivative of the square root of (x + 5)?

    -When using the chain rule for the derivative of the square root of (x + 5), you treat the function as a composite function with the inside function being x + 5 and the outside function being x to the 1/2. Differentiate the outside function to get 1/2 and keep the inside function the same. Then, subtract the exponent by 1 using the power rule, resulting in -1/2. Multiply by the derivative of the inside function, which is 1, to get the final derivative as 1/2 times the square root of (x + 5).

  • What is the derivative of the expression (x^2 - 4)^(1/2)?

    -The derivative of (x^2 - 4)^(1/2) is found by first applying the chain rule. Rewrite the expression, bring the exponent to the front, and subtract the exponent by 1. This gives 1/2 times the derivative of the inside function, which is 2x. So, the derivative is 1/2 times 2x, or x divided by the square root of (x^2 - 4).

  • How do you find the derivative of the cube root of (5x + 2)?

    -To find the derivative of the cube root of (5x + 2), first rewrite the expression using the chain rule. Move the exponent of 1/3 to the front and keep the inside function the same. Subtract the exponent by 1, resulting in 2/3. Multiply by the derivative of the inside function, which is 5, to get the final derivative as 5/3 times the cube root of (5x + 2) squared.

  • What is the process for rationalizing the denominator of a radical expression?

    -To rationalize the denominator of a radical expression, you multiply both the numerator and the denominator by the radical that is in the denominator. This process eliminates the radical from the denominator, resulting in a rationalized expression.

  • What is the derivative of (1/4) * (x^(5/4))?

    -The derivative of (1/4) * (x^(5/4)) is found by applying the power rule. First, move the exponent 5/4 to the front, resulting in -5/4. Then subtract 1 from the exponent, giving -9/4. The final derivative is -5/4 times x to the -9/4 power, divided by 4.

  • How do you differentiate an expression with a radical in the numerator and a constant in the denominator?

    -To differentiate an expression where the numerator is a radical and the denominator is a constant, you first apply the chain rule to the radical part of the numerator. Then, use the constant multiple rule, multiplying the constant by the derivative of the radical expression. Finally, simplify the result by combining terms and converting the rational exponent back into its radical form.

  • What is the final form of the derivative for the expression 8 divided by the seventh root of (3 - 2x) to the fourth power?

    -The final form of the derivative for the expression 8 divided by the seventh root of (3 - 2x) to the fourth power is -64 times the seventh root of (3 - 2x) to the fourth power, divided by 7 times the seventh root of (3 - 2x) to the seventh power.

  • What is the power rule for differentiation?

    -The power rule states that the derivative of x to the power of n, denoted as x^n, is n times x to the power of n minus 1, written as n*x^(n-1).

  • Why is it necessary to convert a rational exponent back to its radical form when differentiating radical functions?

    -Converting a rational exponent back to its radical form is necessary to express the derivative in the same format as the original function. This makes the final answer more understandable and in line with the standard form of radical functions, which is especially important when dealing with square roots, cube roots, and other radical expressions.

  • What is the purpose of the chain rule in differentiation?

    -The chain rule is used to differentiate composite functions, where the outer function is a function of an inner function. It allows you to differentiate the outer function first, treat the inner function as a single entity, and then multiply by the derivative of the inner function. This rule is essential for handling more complex functions where the relationship between the variables is not direct.

  • How does the constant multiple rule apply to the differentiation of an expression with a constant in the numerator and a radical in the denominator?

    -The constant multiple rule states that if there is a constant in the numerator of an expression with a radical in the denominator, the constant is treated as a factor and is multiplied by the derivative of the radical part. This rule helps to simplify the expression and maintain the correct relationship between the variables in the derivative.

Outlines
00:00
📚 Derivative of Radical Functions

This paragraph introduces the concept of finding the derivative of radical functions. It begins with a simple example, the derivative of the square root of x, and explains the process of rewriting the radical expression as a rational exponent. The power rule is reviewed, and the steps to apply it are outlined. The paragraph then demonstrates how to simplify the result and convert it back to radical form. The concept is further applied to the derivative of the square root of (x + 5), using both the power rule and the chain rule. The process is explained step by step, emphasizing the importance of differentiating composite functions and simplifying the final answer.

05:02
🔢 Solving Derivatives of More Complex Radical Expressions

This paragraph continues the discussion on finding derivatives of radical functions, focusing on more complex expressions. It starts with the derivative of the square root of (x^2 - 4), explaining the use of the chain rule and how to simplify the resulting expression. The paragraph then moves on to the derivative of the cube root of (5x + 2), again using the chain rule and providing a detailed explanation of the steps involved. The process of rationalizing the denominator is also discussed, offering an alternative form of the final answer for this example.

10:02
📈 Advanced Derivative Calculations with Rational Exponents

This paragraph delves into advanced derivative calculations involving rational exponents. It begins with the derivative of (1/(x^(5/4))) and explains the process of converting the rational exponent to a radical form. The paragraph then tackles the derivative of a more complex expression, (8/(∛(3 - 2x)^(4/7))), using the chain rule and constant multiple rule. The steps are outlined in detail, including the simplification of the expression and the conversion back to radical form. The paragraph emphasizes the importance of understanding the rules of exponents and radicals in solving these types of derivatives.

15:06
📊 Further Applications of Derivative Rules

The final paragraph of the script is not provided in the input, thus no summary can be generated for it.

Mindmap
Keywords
💡derivative
The derivative is a fundamental concept in calculus that represents the rate of change or the slope of a function at a particular point. In the context of the video, the derivative is used to find how a quantity changes in relation to another, specifically focusing on the behavior of radical functions. The video provides examples of finding derivatives for various radical expressions, such as the square root and cube root of x, illustrating the process of differentiating these functions using the power rule and chain rule.
💡radical functions
Radical functions are mathematical functions that include roots in their expressions, such as square roots, cube roots, and other nth roots. In the video, the focus is on understanding how to find the derivatives of these types of functions, which involves converting radical expressions into rational exponents and then applying the power rule and chain rule to differentiate them. The video demonstrates the process of differentiating radical functions through various examples, emphasizing the importance of rewriting expressions and simplifying results.
💡power rule
The power rule is a basic differentiation rule in calculus that states the derivative of a function f(x) = x^n, where n is a constant, is f'(x) = n * x^(n-1). This rule is fundamental for finding derivatives of functions with exponents and is used extensively in the video when dealing with radical functions. The power rule simplifies the process of finding derivatives by allowing us to treat the exponent as a separate entity that can be manipulated according to the rule.
💡chain rule
The chain rule is a crucial concept in calculus used for differentiating composite functions, which are functions composed of one function nested inside another. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function. In the video, the chain rule is employed to find the derivatives of more complex radical expressions, such as the square root of x + 5 and the cube root of 5x + 2.
💡rational exponent
A rational exponent is an exponent that is a fraction, representing a power that can be expressed as a root. For example, x^(3/4) is the same as the fourth root of x cubed. In the context of the video, rational exponents are used to rewrite radical expressions in a form that allows for easier application of differentiation rules. The process of converting between radical and rational exponents is essential for differentiating radical functions and finding their derivatives.
💡simplify
Simplification in mathematics refers to the process of making a mathematical expression or equation more straightforward or easier to understand. In the context of the video, simplification is an important step after applying differentiation rules to radical functions. It often involves converting rational exponents back into radical form, reducing fractions, and eliminating unnecessary terms to arrive at a clean, final answer.
💡common denominators
A common denominator is a number that is shared by several or all fractions in a given mathematical expression. When fractions have a common denominator, it is possible to combine or compare them more easily. In the video, finding common denominators is a step in the process of simplifying expressions after differentiation, particularly when dealing with terms that have different denominators resulting from the application of differentiation rules.
💡negative exponent
A negative exponent indicates that a term should be taken as the reciprocal when dealing with powers of variables. For example, x^(-n) is equivalent to 1/x^n. Negative exponents often arise in the process of differentiation and require careful handling to ensure the correct simplification of expressions. In the video, negative exponents are encountered when applying the power rule to differentiate radical functions, and they are converted into positive exponents by taking the reciprocal of the base.
💡composite function
A composite function is a function that is created by combining two or more functions in such a way that the output of one function becomes the input of another. In the video, composite functions are discussed in the context of the chain rule, where the derivative of the composite function is found by differentiating the outer function with respect to the inner function's result.
💡differentiate
To differentiate is to find the derivative of a function, which gives the rate of change or the slope of the function at any point. Differentiation is a key process in calculus and is the primary operation discussed in the video. The video focuses on differentiating radical functions, which involves converting them into rational exponents and applying the power rule and chain rule.
💡rationalize the denominator
Rationalizing the denominator is the process of eliminating radicals or irrational numbers from the denominator of a fraction. This is often done to simplify the expression or to prepare it for further calculations. In the video, rationalization is mentioned as an optional step after differentiating certain radical functions, particularly when the result includes a radical in the denominator.
Highlights

The process of finding the derivative of radical functions is discussed.

The derivative of the square root of x is derived by rewriting the radical as a rational exponent and applying the power rule.

For the fifth root of x cubed, the radical is rewritten as x to the three fifths.

The chain rule is introduced for finding the derivative of composite functions.

The derivative of the square root of x plus five is calculated using both the power rule and the chain rule.

The derivative of the square root of x squared minus four is found by applying the chain rule and simplifying the result.

The cube root of 5x plus two is derived by rewriting the expression and using the chain rule.

The process of rationalizing the denominator is explained for the cube root of 5x plus two.

The derivative of one over the fourth root of x to the fifth power is calculated and simplified.

The method of rationalizing the radical form is demonstrated for the derivative of x to the 9/4 power.

The derivative of eight divided by the seventh root of three minus two x to the fourth power is detailed using the chain rule and constant multiple rule.

The final answer for the derivative of eight divided by the seventh root of three minus two x to the fourth power is provided in both radical and rationalized forms.

The importance of practice in improving skills and understanding of calculus is emphasized.

The method of converting rational exponents back to radical form is a key step in deriving radical functions.

The use of common denominators is crucial for simplifying the derivatives of radical functions.

The power rule is reviewed as a fundamental tool for finding derivatives of functions with exponents.

The concept of negative exponents and how to handle them in the context of derivatives is explained.

The process of differentiating composite functions is broken down into manageable steps.

Transcripts

Browse More Related Video

Derivatives of Trig Functions - Calculus | MCV4U

Derivatives - Power Rule

Basic Derivative Rules - Part 2: Combining the Rules

The Power Rule For Derivatives

Derivatives for Beginners - Basic Introduction

Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DerivativeCalculusMathematicsEducationRadicalFunctionsPowerRuleChainRuleRationalExponentsStepByStepGuideMathTutorialsDifferentialCalculusMathematicsTipsEducationalContent