High School Physics - Metric System
TLDRThis script introduces the metric system, emphasizing its importance in physics for accurate communication of real-world measurements. It outlines the seven fundamental units, the convenience of the base-10 system, and how it contrasts with the English system. The script explains the conversion process between different metric units, including fundamental and derived units, and provides examples of such conversions. It also touches on estimating values in the metric system, offering a practical approach to understanding measurements in physics.
Takeaways
- 📏 The metric system is used in physics to standardize measurements and is based on powers of 10, making calculations easier compared to the English system.
- 🔢 It consists of seven fundamental units including the metre (m) for length, kilogram (kg) for mass, and second (s) for time, with derived units like velocity and acceleration.
- 📐 Smaller units than a metre include centimetre (cm), millimetre (mm), micrometer (µm), and nanometer (nm), while larger units include the kilometre (km).
- 📈 Units of mass smaller than a kilogram are grams (g) and milligrams (mg), while larger units include the mega gram and metric tonne, both equivalent to 1000 kilograms.
- ⏱️ Time units in the metric system are not always based on powers of 10, with minutes, hours, and years being examples of larger units.
- 🔄 Conversion between metric units is done using reference tables and mathematical operations, such as multiplying or dividing by powers of 10.
- 🚀 Derived units are composed of combinations of fundamental units, such as meters per second (m/s) for velocity and Newtons (N) for force, which is equivalent to kg·m/s².
- 📊 Estimating values in the metric system can be done by comparing known quantities, such as approximating the length of a football field to 100 meters or a marathon to 44 kilometers.
- 📝 Practice is key to mastering metric conversions, and using online tools can help verify the accuracy of conversions.
- 📚 Additional resources like physics guides and online platforms offer more examples and practice problems for learning and applying metric system conversions.
Q & A
What is the primary purpose of the metric system in the context of physics?
-The primary purpose of the metric system in physics is to provide a standardized set of units for accurate communication and quantification of measurements, facilitating the study, prediction, and analysis of real-world phenomena.
How does the metric system differ from the English system in terms of mathematical ease?
-The metric system is based on powers of 10, which makes mathematical operations easier compared to the English system, which lacks a consistent standard and includes units like 12 inches in a foot, 3 feet in a yard, and 5,280 feet in a mile.
What are the seven fundamental units of the metric system?
-The seven fundamental units of the metric system are the meter (m) for length, kilogram (kg) for mass, second (s) for time, ampere (A) for electric current, kelvin (K) for temperature, mole (mol) for amount of substance, and candela (cd) for luminous intensity.
How is the meter related to smaller units of length?
-The meter is the base unit of length in the metric system. Smaller units include the centimeter (cm), millimeter (mm), micrometer (µm), and nanometer (nm), which are powers of 10 smaller than a meter.
What are the larger units of mass in the metric system?
-Larger units of mass in the metric system include the kilogram (kg), gram (g), and milligram (mg) for smaller masses, and the mega gram (Mg) and metric tonne (t) for very large masses, with 1 metric tonne being equivalent to 1,000 kilograms.
How does the metric system handle time measurements that are not based on powers of 10?
-While the base unit of time is the second and smaller units like milliseconds and microseconds follow powers of 10, larger units such as minutes, hours, and days do not strictly adhere to powers of 10, with 60 seconds in a minute, 60 minutes in an hour, and 24 hours in a day.
What is an example of a derived unit in the metric system?
-An example of a derived unit is velocity, which is measured in meters per second (m/s), and acceleration, which is measured in meters per second squared (m/s²). Force is another derived unit, measured in Newtons (N), which is equivalent to a kilogram times a meter per second squared (kg·m/s²).
How can you convert 248 meters to kilometers?
-To convert 248 meters to kilometers, you would divide the number of meters by 10 to the third power (1,000), which gives you 0.248 kilometers.
What is the process for converting 5375 kilograms to grams?
-To convert 5375 kilograms to grams, you would multiply the number of kilograms by 10 to the third power (1,000) to get grams, resulting in 5,375,000 grams.
How many seconds are there in a year?
-There are approximately 31,557,600 seconds in a year, calculated by multiplying 365.25 (days in a year) by 24 (hours in a day) by 60 (minutes in an hour) by 60 (seconds in a minute).
How can you estimate the length of a football field in meters?
-A football field is approximately 100 yards in length. Since a yard is roughly equivalent to a meter, you can estimate the length of a football field to be around 100 meters.
How would you estimate the mass of an average student in kilograms?
-An average student might weigh around 150 pounds. Since there are roughly 2.2 pounds in a kilogram, you could estimate the student's mass to be around 68 kilograms (150 / 2.2).
Outlines
📏 Introduction to the Metric System
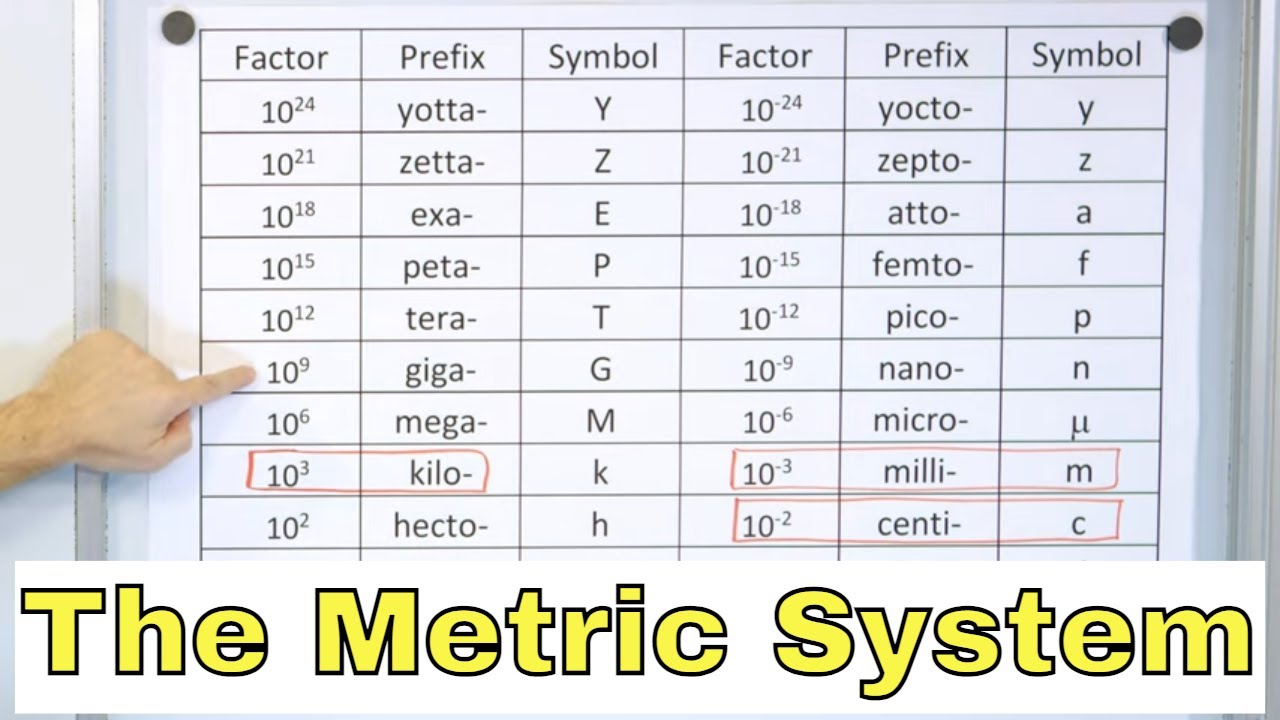
This paragraph introduces the concept of the metric system and its importance in physics. It explains the need for standardized units to accurately communicate observations and measurements in the real world. The metric system, also known as the International System of Units (SI), is highlighted as the standard used by physicists and is based on seven fundamental units derived from powers of 10. This makes calculations easier compared to the English system, which lacks a consistent standard. The paragraph emphasizes the use of meters (m) for length, kilograms (kg) for mass, and seconds for time, with a brief mention of the ampere as a unit for electric current. It also outlines the metric prefixes for smaller and larger units of length and mass, providing examples of their real-world applications.
🔄 Unit Conversion in the Metric System
This paragraph delves into the process of converting units within the metric system. It explains the method of using reference tables to understand the meaning of metric prefixes and how to convert between different units. The paragraph provides step-by-step examples of converting meters to kilometers and kilograms to grams, emphasizing the use of powers of 10 and the process of canceling out units. It also introduces the concept of two-step conversions, using the example of converting milliseconds to nanoseconds. The paragraph aims to help users understand and apply the principles of unit conversion in the metric system.
🏃♂️ Derived Unit Conversion and Estimation
This paragraph focuses on derived unit conversions and estimation in the metric system. It explains how to convert derived units such as velocity from meters per second to kilometers per hour, using the same conversion principles discussed earlier. The paragraph also provides examples of estimating values in the metric system, such as the length of a football field, the mass of a student, and the length of a marathon. It encourages users to practice conversions on their own and to verify their results using online tools or resources like Google. The paragraph concludes with a suggestion to consult additional resources for more sample problems and information on the metric system.
📚 Additional Resources for Learning
In this final paragraph, the speaker provides additional resources for those interested in learning more about the metric system and its applications. The paragraph briefly mentions the availability of more sample problems and comprehensive guides in resources such as 'a plus physics comm' or 'a plus physics your guide to regents physics essentials'. These resources are recommended for users to further enhance their understanding and practice of unit conversions and estimations within the metric system.
Mindmap
Keywords
💡Metric System
💡Fundamental Units
💡Derived Units
💡Conversion
💡Prefixes
💡Estimation
💡Physics
💡English System
💡Length
💡Mass
💡Time
Highlights
The importance of the metric system in physics for accurate communication of measurements.
The metric system is based on seven fundamental units and powers of 10, making calculations easier compared to the English system.
The metre (m) is the basic unit of length in the metric system, similar to a yard in the English system.
Smaller length units include centimeters (cm), millimeters (mm), micrometers (µm), and nanometers (nm).
Larger length units include kilometers (km), which are slightly more than half a mile.
The kilogram (kg) is the base unit of mass, roughly equivalent to 2.2 pounds in the English system.
Smaller mass units include grams (g) and milligrams (mg), while larger units include megagrams and metric tonnes.
The base unit of time in the metric system is the second, with smaller units like milliseconds (ms) and microseconds (µs).
Derived units are combinations of fundamental units, such as velocity in meters per second (m/s) and acceleration in meters per second squared (m/s²).
Force is measured in Newtons, which is equivalent to a kilogram times a meter per second squared (kg·m/s²).
Conversion between units is facilitated by a reference table of metric prefixes and their corresponding powers of 10.
A step-by-step procedure for unit conversion is demonstrated, such as converting meters to kilometers and kilograms to grams.
Two-step conversions are explained, like converting milliseconds to nanoseconds.
Derived unit conversions are also explained, such as changing meters per second to kilometers per hour.
Estimating values in the metric system is discussed, with examples like the length of a football field and the mass of a student.
The length of a marathon is estimated to be around 44 kilometers using the metric system.
The mass of a paper clip is estimated to be around one gram.
The method of converting years to seconds is demonstrated, resulting in approximately 3.16 × 10^7 seconds in one year.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: