Converting Metric Units

Mr. Kohne
21 Mar 202008:55
EducationalLearning
32 Likes 10 Comments

TLDRThe script introduces the metric system, emphasizing its base-10 structure and the importance of understanding the basic units of gram, meter, and liter, as well as their larger and smaller counterparts. It explains the method of converting between units by moving the decimal pointη›ΈεΊ” to the unit prefix, using the acronym 'King Henry died unexpectedly drinking chocolate milk' to remember the order of metric units. The process is demonstrated with examples, highlighting the simplicity of converting between units by adjusting the decimal point and appending zeros as necessary.

Takeaways
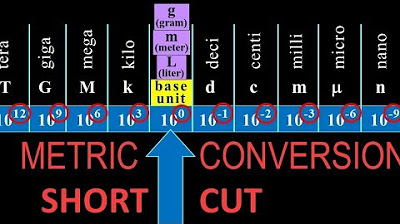
  • πŸ“ The metric system is based on three fundamental units: gram (mass), meter (length), and liter (volume).
  • πŸ”’ There are both larger and smaller units derived from the basic metric units with different prefixes such as kilo-, hecto-, deca-, deci-, centi-, milli-.
  • 🌐 The metric system operates on a base-10 structure, meaning each unit to the left is ten times greater than the one to its right.
  • πŸ”„ Conversion between metric units involves moving the decimal point to account for the scale change, effectively multiplying or dividing by powers of ten.
  • πŸ“ˆ To convert from a larger to a smaller unit, move the decimal point to the right and append zeros as needed to fill in the value places.
  • πŸ“‰ To convert from a smaller to a larger unit, move the decimal point to the left and remove unnecessary zeros after the decimal point.
  • πŸ’‘ Acronyms like 'King Henry Died Unexpectedly Drinking Chocolate Milk' can help remember the order of metric prefixes from largest to smallest.
  • 🎯 When converting, it's crucial to identify the correct starting unit and the desired ending unit based on the context of the problem.
  • πŸ”Ž Pay attention to the presence of decimals in the given values and adjust the starting position of the decimal point accordingly during conversion.
  • 🌟 The process of converting units is essentially moving between the basic units (u) and understanding the mathematical relationship between them.
  • βš™οΈ Examples provided in the script demonstrate how to move the decimal point based on the scale of the units, whether converting to a larger or smaller unit.
Q & A

  • What are the three basic metric units mentioned in the script?

    -The three basic metric units mentioned are gram, meter, and liter.

  • What does the prefix 'kilo' represent in the metric system?

    -The prefix 'kilo' represents a factor of one thousand in the metric system, as in kilogram or kilometer.

  • What is the base-10 property of the metric system?

    -The base-10 property of the metric system means that units to the left are ten times greater than the units to the right, and units to the right are one-tenth of the units to the left.

  • How can you convert a larger unit to a smaller unit in the metric system?

    -To convert a larger unit to a smaller unit, you multiply by the factor of 10 corresponding to the number of unit divisions. For example, to convert kilograms to grams, you multiply by 1000.

  • How do you remember the order of metric units?

    -One mnemonic device to remember the order of metric units is the phrase 'King Henry died unexpectedly drinking chocolate milk,' which helps recall the prefixes in order.

  • What is the process for converting milliliters to liters?

    -To convert milliliters to liters, you move the decimal point three places to the left and fill in any blank spaces with zeros. For example, 39.5 milliliters is 0.0395 liters.

  • How can you convert centimeters to meters?

    -To convert centimeters to meters, you move the decimal point two places to the left because there are 100 centimeters in a meter. For example, 237 centimeters is 2.37 meters.

  • What is the significance of the 'U' in the script when discussing metric units?

    -The 'U' stands for 'basic units' in the script, representing the fundamental units of gram (g), meter (m), and liter (L) in the metric system.

  • How can you convert kilometers to millimeters?

    -To convert kilometers to millimeters, you move the decimal point six places to the left because there are 1,000,000 millimeters in a kilometer. For example, 78 kilometers is 78,000,000 millimeters.

  • What is the importance of moving the decimal point when converting metric units?

    -Moving the decimal point is important because it allows you to quickly and accurately convert between metric units by multiplying or dividing by powers of 10, which simplifies the calculation process.

  • Why is it important to be careful with units that have similar abbreviations?

    -It is important to be careful with similar abbreviations because they can be easily confused, leading to incorrect conversions. For example, 'm' can stand for both 'meter' and 'milli', so understanding the context is crucial.

Outlines
00:00
πŸ“ Introduction to Metric Units and Conversion Basics

This paragraph introduces the concept of metric units and the importance of understanding them for conversion purposes. It outlines the three basic metric units: gram, meter, and liter, and explains the existence of both larger and smaller units derived from these with different prefixes. The paragraph emphasizes the base-10 nature of the metric system, highlighting how units to the left are ten times greater than those to the right, and vice versa when moving in the opposite direction. It also introduces a mnemonic device, 'King Henry died unexpectedly drinking chocolate milk,' to remember the order of metric units, and provides an example of converting kilograms to grams by moving the decimal point accordingly.

05:01
πŸ“ Converting Smaller Units to Larger Units

This paragraph delves into the process of converting smaller units to larger ones, using the example of converting centimeters to meters. It cautions against confusing similar-sounding units, such as meters and millimeters, and reiterates the base-10 principle of the metric system. The paragraph explains how to move the decimal point to the left to convert from a smaller to a larger unit, and provides a step-by-step example of converting 237 centimeters to meters, resulting in 2.37 hundredths of a meter. It also encourages practice with more examples to solidify understanding of the conversion process.

Mindmap
Keywords
πŸ’‘Metric Units
Metric units are standardized units of measurement used globally, primarily in science, industry, and medicine. The video introduces metric units as fundamental to learning conversions within the system. Examples of basic metric units mentioned are grams, meters, and liters, which serve as the foundational units for mass, length, and volume, respectively. The script emphasizes understanding these units to effectively engage in conversions like changing meters to kilometers or grams to kilograms.
πŸ’‘Prefixes
In the metric system, prefixes are used to denote multiples or fractions of the basic units. The video discusses prefixes like 'kilo-', 'hecta-', 'deca-', 'deci-', 'centi-', and 'milli-', which modify the base units to indicate magnitudes either larger or smaller than the base unit by powers of ten. These prefixes help in scaling the units up or down, essential in converting units, such as kilogram being 1000 times a gram.
πŸ’‘Base-10 System
The metric system is described as a 'base-10 system' in the video, meaning each step up or down in unit magnitude involves multiplying or dividing by ten. This system's simplicity facilitates easier calculation and conversion across different scales of measurement. The video uses this concept to explain how moving from meters to kilometers involves multiplying by powers of ten, aligning with the system's base-10 nature.
πŸ’‘Conversion
Conversion in the context of the video refers to the process of changing a measurement from one unit to another within the metric system. The script illustrates conversions through examples, showing how to use the position of decimal points and the number of places moved to convert between units, such as converting kilograms to grams or centimeters to meters.
πŸ’‘Decimal Point Movement
The movement of the decimal point is a critical concept in metric conversions explained in the video. As the metric system is a base-10 system, converting between units often requires simply moving the decimal point left or right depending on whether one is scaling up or down. The video provides practical examples, like converting 1 kilogram to 1000 grams by moving the decimal three places to the right.
πŸ’‘Acronyms
Acronyms are mnemonic devices used to aid memory, as illustrated by the video's use of 'King Henry Died Unexpectedly Drinking Chocolate Milk'. This acronym helps viewers remember the order of metric prefixes from kilo to milli, which is crucial for proper unit conversion. Such mnemonics make it easier to recall complex sequences or lists, enhancing learning efficiency.
πŸ’‘Kilogram
A kilogram is a unit of mass in the metric system and one of the base units mentioned in the video. The script explains how a kilogram is larger than a gram and serves as a starting point for understanding larger units of mass. The kilogram is used as an example to demonstrate how to convert into smaller units (grams) by using decimal point movements.
πŸ’‘Milliliter
Milliliter is a unit of volume in the metric system, typically used to measure smaller liquid quantities. The video uses milliliters to show conversions to liters, emphasizing understanding of conversions from smaller to larger volume units. The discussion includes moving the decimal point to convert 39.5 milliliters to liters, illustrating the practical application of the base-10 system.
πŸ’‘Hectometer
A hectometer, although less commonly used, is a metric unit of length mentioned in the video. It represents one hundred meters. The video includes hectometers when discussing larger scale conversions, such as converting meters to hectometers, to demonstrate the broad range of measurements that can be accommodated within the metric system.
πŸ’‘Multiplying by Powers of 10
Multiplying by powers of 10 is a fundamental operation in the metric system, as highlighted in the video. This approach simplifies the process of conversion by utilizing the base-10 system's structure. The video demonstrates this through examples, where converting larger to smaller units or vice versa involves multiplying or dividing the quantities by 10, 100, or 1000, depending on the unit change.
Highlights

Introduction to metric unit conversion

Three basic metric units: gram, meter, liter

Explanation of larger and smaller metric units with prefixes

The metric system is a base-10 system

Conversion involves multiplying or dividing by powers of 10

Using the acronym 'King Henry died unexpectedly drinking chocolate milk' to remember metric units order

Example of converting kilograms to grams

Explanation of how to move the decimal point in conversion

Example of converting centimeters to meters

Clarification on distinguishing between similar metric units like meters and millimeters

Example of converting milliliters to liters with an existing decimal

Guidance on starting the decimal point movement from the existing decimal place

Example of converting kilometers to millimeters with a large unit jump

Counting the number of spaces to move the decimal point for large unit conversions

Filling in zeros when moving the decimal point results in blank spaces

Transcripts

Browse More Related Video

Shortcut for Metric Unit Conversion

metric unit conversions shortcut: fast, easy how-to with examples

High School Physics - Metric System

Metric Units of Mass | Convert mg, g, and kg

Converting Metric Units Of Measure For Dosage Calculation | @LevelUpRN

How to Convert Units in Chemistry

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MetricConversionMathematicsScienceEducationUnitConversionBase-10SystemKGtoGramsMeterstoCentimetersLiteratureDecimalPointMovementEducationalContent