AP Physics Workbook 7.D Forces vs Torques
TLDRThe video script discusses a physics problem involving torque and rotation, specifically focusing on a box tied to a rope around a pulley. The scenario describes the box's motion as it initially moves upward, stops, and then moves downward. The forces acting on the box and the pulley are analyzed, including gravity, tension, and the normal force. The key takeaway is understanding how the force of tension creates a net torque on the pulley, causing it to rotate. The problem also involves sketching the angular velocity as a function of time, highlighting the change from counterclockwise to clockwise motion and the corresponding angular acceleration.
Takeaways
- 📚 The scenario involves a box of mass M tied to a rope wrapped around a pulley, initially rotating clockwise and pulling the box upwards.
- 🔽 The box initially moves upward, slows down, stops, and then moves back downwards due to the net force acting on it.
- 🎨 When drawing a Freebody diagram, label the forces acting on the box, such as gravity pulling it down and the tension in the rope.
- 🔄 The pulley experiences a net torque due to the force of tension in the rope, which causes it to rotate.
- 🔽 The force of gravity acts downwards on both the box and the pulley, but it's the tension force that contributes to the rotational torque.
- 📊 To graph the angular velocity as a function of time, consider the direction of rotation (counterclockwise is positive, clockwise is negative).
- 🚫 The box's angular velocity starts positive (counterclockwise), becomes zero (stops), and then goes negative (clockwise) as it moves downward.
- 📉 The angular acceleration can be determined by taking the derivative or slope of the angular velocity graph.
- 🔄 The pulley's rotation is driven by the tension force, which creates a torque when it is applied at a distance from the axis of rotation.
- 📈 The angular velocity graph shows a linear change in angular velocity, reflecting a constant angular acceleration.
- 📚 Understanding the relationship between force diagrams and torque is crucial for solving problems involving rotational motion.
Q & A
What is the scenario described in the transcript?
-The scenario involves a box of mass M tied to a rope that is wrapped around a pulley. The pulley is initially rotating clockwise and is planned to pull the box upwards. The box slows down, stops, and then moves back downwards.
What are the forces acting on the box initially?
-Initially, the forces acting on the box include gravity pulling it downwards and the tension in the rope pulling it upwards. The force normal (opposite to gravity) is also present.
Why does the box move back downwards after stopping?
-The box moves back downwards after stopping because there is a net force acting downwards, which is the force of gravity overcoming the force tension from the rope.
What is the role of the pulley in this scenario?
-The pulley is a central rotating object around which the rope is wrapped. It experiences forces from the rope (tension force) and the force of gravity acting on the box.
What force is responsible for the net torque on the pulley?
-The net torque on the pulley is caused by the force of tension in the rope. This is because the force of gravity acts vertically downwards, but the tension force is applied at a distance from the axis of rotation, creating a torque.
How does the angular velocity of the pulley change over time?
-The angular velocity of the pulley starts positive (counterclockwise) as it is initially rotating counterclockwise. It then stops instantaneously and changes direction, becoming negative (clockwise) as the box moves back downwards.
What is the relationship between angular velocity and angular acceleration?
-Angular acceleration is the derivative of angular velocity with respect to time. It represents the rate of change of the angular velocity, indicating whether the velocity is increasing or decreasing.
How is the slope of the angular velocity-time graph related to angular acceleration?
-The slope of the angular velocity-time graph represents the angular acceleration. A positive slope indicates positive angular acceleration (speeding up), while a negative slope indicates negative angular acceleration (slowing down).
What are the units for angular velocity (Omega) and angular acceleration (Alpha)?
-Angular velocity (Omega) is measured in radians per second (rad/s) and angular acceleration (Alpha) is measured in radians per second squared (rad/s^2).
How can the direction of rotation be determined in the context of this problem?
-In this problem, counterclockwise rotation is considered positive, while clockwise rotation is considered negative. This convention is used to analyze the changes in the pulley's angular velocity.
Outlines
📚 Introduction to Torque and Rotations in AP Physics
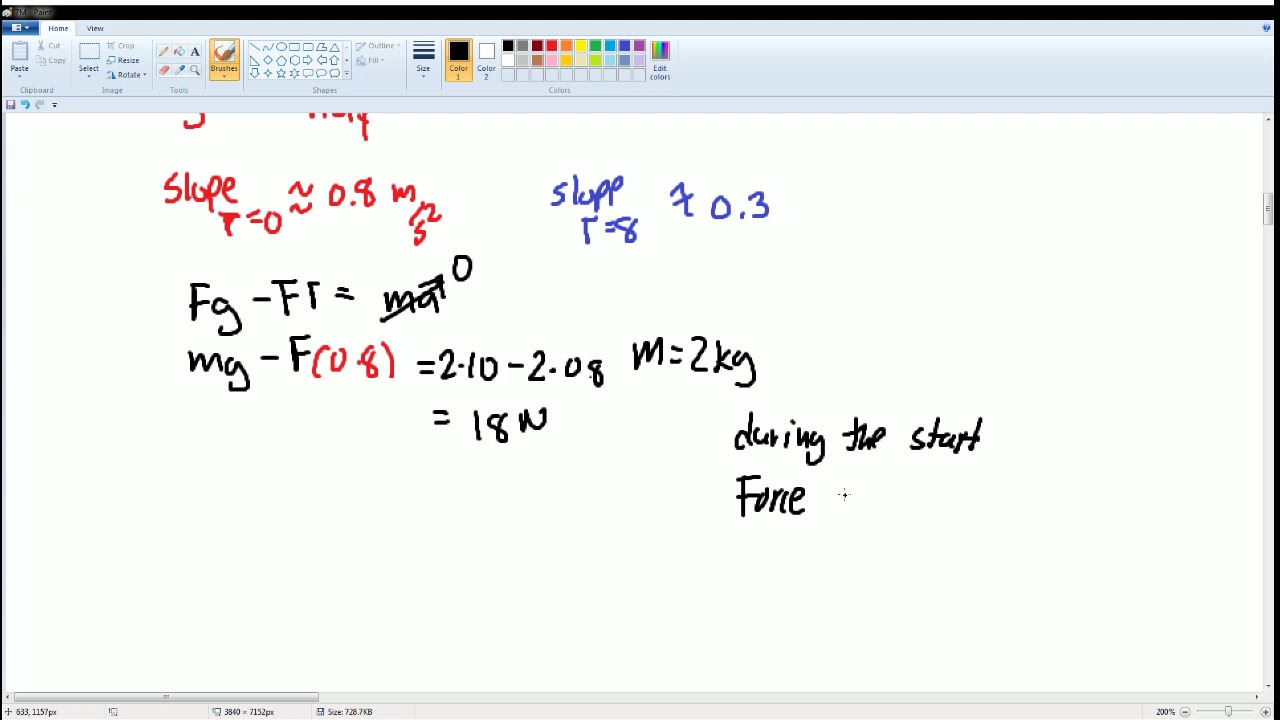
This paragraph introduces the topic of unit 7, which focuses on torque and rotations in the context of AP Physics. The scenario described involves a box of mass M tied to a rope wrapped around a pulley. Initially, the pulley is rotating clockwise, and the rope is pulling the box upwards. However, the box eventually slows down, stops, and moves back downwards. The paragraph emphasizes the importance of drawing a Freebody diagram to represent and label the forces acting on the box, treating it as a point particle for simplicity. It discusses the forces of gravity and tension, and how they affect the box's motion. The key point is understanding the net force that causes the box to move downwards and how the forces change as the box's motion changes.
🔄 Analyzing Torque and Angular Velocity in a System
This paragraph delves deeper into the concept of torque and its relationship with angular velocity in a physical system. It explains why torque exists due to the force of tension being applied at a distance (R value) from the center of the pulley, which is the axis of rotation. The net torque is caused by the force of tension, which is responsible for the pulley's rotation. The paragraph then describes the process of sketching the angular velocity as a function of time, starting from the initial instance when the system is in motion until it returns to its original height. It highlights the importance of understanding the direction of rotation (counterclockwise being positive and clockwise being negative) and how to convert angular velocity into angular acceleration through differentiation or slope calculation. The summary concludes with a brief mention of the symbols used for angular velocity (Omega) and angular acceleration (alpha).
Mindmap
Keywords
💡Torque
💡Rotation
💡Force
💡Freebody Diagram
💡Pulley
💡Gravity
💡Tension
💡Axis of Rotation
💡Angular Velocity
💡Angular Acceleration
Highlights
The scenario involves a box of mass M tied to a rope wrapped around a pulley, which is initially rotating clockwise and pulling the box upwards.
The box initially moves upwards, slows down, stops, and then moves back downwards.
A Freebody diagram should be drawn to represent and label the forces exerting on the box, treating it as a point particle for simplicity.
The forces on the box include gravity pulling it down and the tension in the rope pulling it up.
The force normal to the box should be slightly smaller than the force of gravity to allow for the box's downward motion.
On the pulley, the forces include gravity, the normal force, and the tension force, with the latter being responsible for the net torque.
The net torque on the pulley is caused by the force of tension, as it is the force applied at a distance from the axis of rotation.
The pulley's rotation is caused by the force of tension, which is the only force contributing to the net torque.
A graph of angular velocity as a function of time is to be sketched from the initial instance until the weight comes back down to the same height.
Counterclockwise rotation is considered positive, while clockwise is negative.
The angular acceleration is derived from the slope of the angular velocity-time graph.
The slope of the angular velocity-time graph indicates the rate of change of angular velocity.
The angular velocity initially has a positive value due to the counterclockwise rotation.
When the box stops and starts moving downwards, the angular velocity becomes negative, indicating clockwise motion.
The angular acceleration is flat when the box is not rotating, showing a net slope of zero.
The relationship between angular velocity (Omega) and angular acceleration (Alpha) is derived from the slope of the velocity-time graph.
The solutions provided are based on the force diagram and torque analysis, offering a comprehensive understanding of the system's dynamics.
The explanation of torque and its effect on the pulley's rotation is a key concept in understanding the physics of the scenario.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: