6 Pulley Problems
TLDRIn this educational video, Physics Ninja tackles six diverse pulley problems commonly found in AP and undergraduate physics. Assuming negligible pulley mass and rope weight, the video demonstrates step-by-step solutions focusing on calculating acceleration and tension. The host guides viewers through Newton's second law applications, force diagrams, and algebraic manipulations to solve each problem. The video caters to those seeking to understand the principles of pulley systems and improve problem-solving skills in physics.
Takeaways
- 📚 The video is an educational tutorial focused on solving six different pulley problems, commonly found in AP Physics and undergraduate physics.
- 🔁 The key approximation made in these problems is that the mass of the pulley is negligible compared to the mass of the blocks, and the mass or weight of the rope is also neglected.
- 📉 The video aims to calculate the acceleration and tension in various pulley systems, which are essential for understanding the dynamics of the systems.
- 📚 The first problem involves a block of Big M connected to another of little m, with no friction considered between the surface and the block, simplifying the problem.
- 🔄 The method used to solve the problems involves creating free body diagrams for each mass, identifying all forces acting on them, and applying Newton's second law.
- 🔢 In the problems, the tension in the rope is assumed to be uniform everywhere due to the negligible mass of the pulley, which simplifies the calculations.
- 📈 The tutorial demonstrates how to set up equations for the system's acceleration and tension, and how to solve these equations by adding them to eliminate the tension variable.
- 🤔 The video encourages viewers to think about what would happen if certain conditions change, such as the mass of the blocks or the presence of friction, to understand the physical implications.
- 🔍 The process involves breaking down forces into components, especially when dealing with inclined planes, and considering the normal force in addition to the tension and weight.
- 📉 The tutorial also covers problems with multiple pulleys, emphasizing the advantage of using such systems to distribute forces and reduce the effort needed to lift heavy objects.
- 💪 The final problems illustrate how to calculate the force required to either maintain a constant speed or to accelerate a mass upward using a pulley system.
Q & A
What is the key approximation made in all the pulley problems discussed in the video?
-The key approximation made in all the pulley problems is that the mass of the pulley is negligible compared to the mass of the blocks, and the mass or the weight of the rope is also neglected.
What is the primary focus of the problems in the video?
-The primary focus of the problems in the video is to calculate the acceleration and tension in various pulley systems, assuming ideal conditions with negligible pulley mass and rope weight.
In the first problem, how is the system expected to behave when released from rest?
-In the first problem, with no friction and given the masses of the blocks, it is expected that the larger block (Big M) will accelerate to the right and the smaller block (little m) will accelerate downward when released from rest.
What is the significance of the tension being uniform everywhere on the rope in the problems discussed?
-The significance of the tension being uniform everywhere on the rope is that it simplifies the calculation of forces acting on the blocks, as the tension in the rope does not change regardless of the point where it is considered.
How does the video approach solving for acceleration and tension in the pulley problems?
-The video approaches solving for acceleration and tension by using Newton's second law for both blocks involved in the system, setting up equations based on the forces acting on each block, and then solving the system of equations.
What is the result of the acceleration for the first problem if big M is 10 kg and little m is 1 kg?
-For the first problem, with big M being 10 kg and little m being 1 kg, the acceleration is calculated to be approximately 0.89 meters per second squared.
How does the presence of a slope affect the forces acting on a block in the pulley system?
-The presence of a slope introduces a component of the weight force acting perpendicular to the ramp and another component acting parallel to the ramp, which affects how the block accelerates along the slope.
What is the normal force in a pulley system with a block on a slope, and how does it relate to the weight of the block?
-The normal force in a pulley system with a block on a slope is equal to the component of the weight of the block acting perpendicular to the slope, which is mg cos(theta), where mg is the weight and theta is the angle of the slope.
In the video, how is the tension in the rope calculated for a system with a single string and two pulleys?
-In the video, the tension in the rope for a system with a single string and two pulleys is calculated by considering the forces acting on the block (or system of blocks) and solving for the tension force F, which is the same throughout the entire rope due to the negligible mass of the pulleys and rope.
What is the advantage of using a pulley system with multiple ropes attached to a single force application?
-The advantage of using a pulley system with multiple ropes attached to a single force application is that it distributes the force, allowing for a smaller applied force to support or move a heavier load, effectively multiplying the applied force by the number of rope segments.
How does the video script handle the calculation of forces and accelerations when the system is required to move at a constant speed or accelerate?
-The video script handles the calculation by setting the acceleration to zero for constant speed scenarios, which simplifies the Newton's second law equations to a balance of forces. For acceleration scenarios, the script includes the acceleration in the equations to find the net force and then solves for the required applied force.
Outlines
📚 Introduction to Pulley Problems
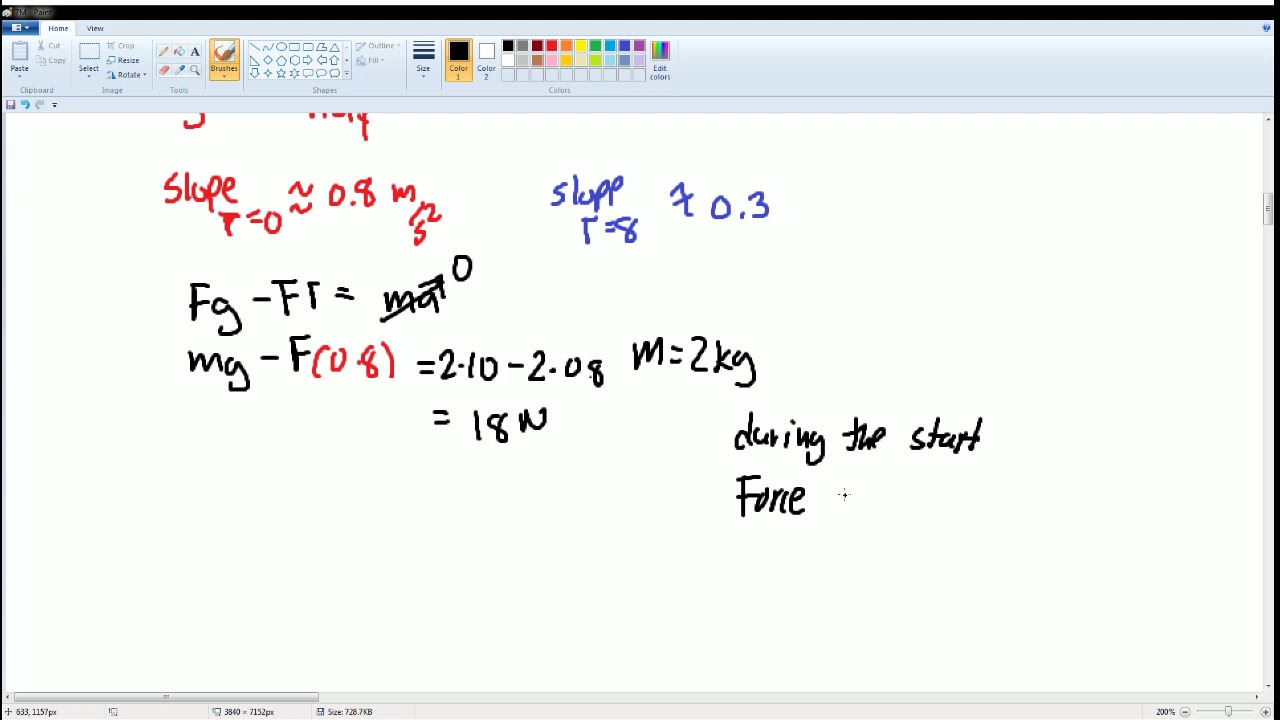
Physics Ninja introduces a series of six pulley problems commonly found in AP and undergraduate physics. The key assumption made in these problems is that the mass of the pulleys is negligible compared to the mass of the blocks, and the weight of the rope is also neglected. The focus is on calculating acceleration and tension within the system. The first problem involves two blocks of different masses connected by a rope over a pulley, with friction neglected. A free body diagram is used to determine the forces acting on each block, and Newton's second law is applied to find the acceleration and tension. The masses are hypothetically set to 10 kg for the large block and 1 kg for the small block.
🔍 Solving Pulley Problems with Uniform Tension
The second paragraph delves into the process of solving pulley problems by identifying the forces involved and applying Newton's second law. It discusses a scenario where both blocks are hanging directly from a single rope, moving up and down. The solution involves creating free body diagrams for each mass, identifying the weight, tension, and normal forces. The tension is found to be uniform due to the negligible mass of the pulley. By adding the equations of motion for both blocks and canceling out the tension, an expression for acceleration is derived. The problem is solved by substituting given values to find the acceleration and tension, demonstrating a systematic approach to solving pulley problems.
📐 Pulley Systems with Inclined Planes
This section introduces a variation of the pulley problem where one block is on an inclined plane. The forces acting on the blocks are broken down into components, considering the angle of the incline. The weight of the blocks is decomposed into components perpendicular and parallel to the ramp. Newton's second law is applied in both the x and y directions for the block on the slope, and in the vertical direction for the hanging block. By adding the equations for both blocks and eliminating the tension, an expression for the acceleration of the system is obtained. The solution involves substituting the given masses and angle to find the acceleration and tension in the rope.
🔄 Advanced Pulley Configurations
The script continues with a more complex pulley system involving a single string wrapping around a pulley with a suspended block. The problem is simplified by considering the entire setup as a single system, with all forces acting on it. The tension in the rope is uniform throughout due to the negligible mass of the pulley and rope. The first scenario involves lowering the block at a constant speed, requiring a force F that is half the weight of the block due to the mechanical advantage provided by the pulley system. The second scenario involves accelerating the block upward, necessitating a greater force F to overcome the weight and provide the desired acceleration.
🚀 Solving for Acceleration and Force in Complex Pulley Systems
The final paragraph presents a complex pulley system with six pulleys and a 300 kg mass. The objective is to determine the force required to either lower or raise the mass at a constant speed, and to accelerate it upward. By placing the system within a conceptual 'box', all forces acting on the box are considered, including the weight of the mass and the tension in the ropes. For constant speed, the force applied (F) is equal to the weight divided by the number of ropes (six), leveraging the mechanical advantage of the pulley system. To achieve upward acceleration, the force F must be greater, calculated by considering the mass, desired acceleration, and gravitational acceleration, and then divided by the number of ropes.
Mindmap
Keywords
💡Pulley
💡Friction
💡Mass
💡Acceleration
💡Tension
💡Newton's Second Law
💡Atwood Machine
💡Free Body Diagram
💡Slope
💡Normal Force
💡Component
Highlights
Six pulley problems are discussed with a focus on AP Physics and undergraduate physics.
The mass of the pulley is considered negligible compared to the mass of the blocks.
The weight of the rope is neglected in the calculations.
The acceleration and tension in the system are the primary calculations.
Problem 1 involves a block of Big M connected to another of little m with no friction.
Free body diagrams are used to determine the forces acting on each block.
Newton's second law is applied to calculate the acceleration of the blocks.
The tension in the rope is found to be uniform due to the negligible mass of the pulley.
Problem 2 features both masses hanging directly with a focus on up and down movement.
An Atwood machine setup is used to derive expressions for acceleration and tension.
Problem 3 introduces a block on a slope with a focus on component forces.
The normal force and its relation to the weight of the blocks are discussed.
Problem 4 involves a single string and multiple pulleys, emphasizing the force distribution.
The effect of multiple ropes on the force required to move a block is calculated.
Problem 5 with a large mass and multiple pulleys demonstrates the advantage of pulley systems.
The force required to accelerate a mass upward using a pulley system is calculated.
A step-by-step approach to solving pulley problems is provided, emphasizing the importance of Newton's laws.
The video concludes with a summary of the methods used to solve pulley problems.
Transcripts
Browse More Related Video

Treating systems (the hard way) | Forces and Newton's laws of motion | Physics | Khan Academy

2019 AP Physics 1 Solutions Free Response #2
AP Physics Workbook 7.M Massive Pulley
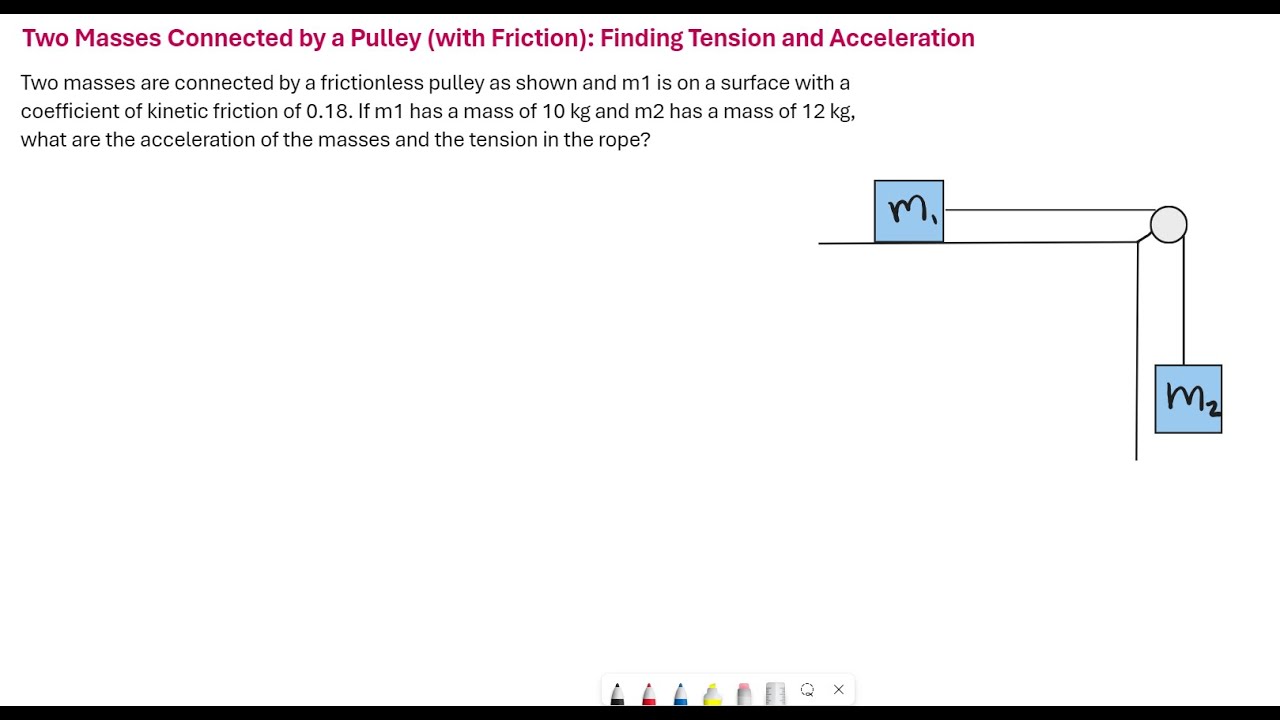
Finding the Tension and Acceleration for a Two Mass Pulley (with Friction)

2019 #2 Free Response Question - AP Physics 1 - Exam Solution
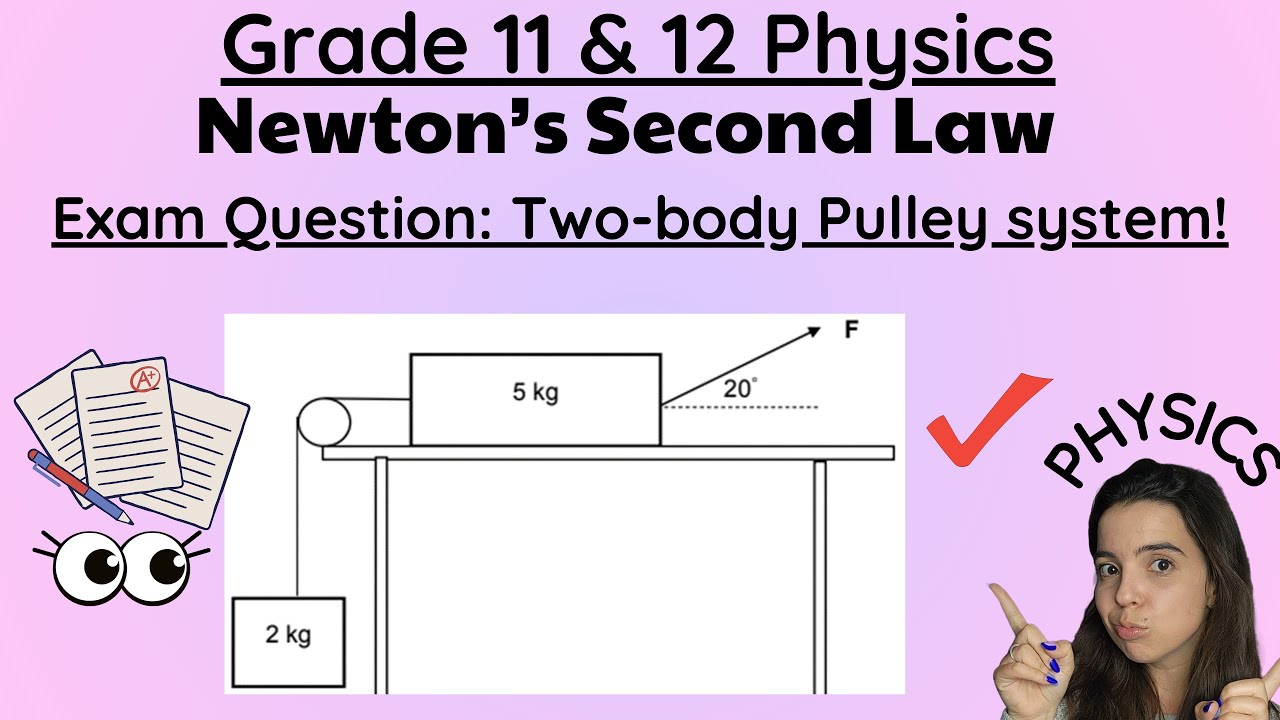
Newton's Second Law Exam Question: Two-body systems Pulley practice
5.0 / 5 (0 votes)
Thanks for rating: