AP Physics Workbook 3.K Friction as the Centripetal Force
TLDRThe video script outlines an experiment to determine the coefficient of static friction (μs) between a coin and a steel plate. A student measures the distance (R) from the center of rotation to the coin and the period (t) of the plate's rotation. By gradually increasing the rotation speed and recording the critical speed at which the coin slips, the student can calculate the centripetal force required to keep the coin in circular motion. Using Newton's second law and the derived equation relating T squared to R and μG, the student can plot a graph and calculate the static friction coefficient. The process emphasizes the importance of accurate measurements and reducing experimental error, suggesting the use of electronic devices for precise timing.
Takeaways
- 📚 The problem involves determining the coefficient of static friction (μs) between a coin and a steel plate using circular motion and gravitation principles.
- 🔍 The student measures the distance (R) from the center of rotation to the coin and the period (t) of the plate's rotation to gather data for calculations.
- 💡 The centripetal force required for the coin to maintain circular motion is provided by the force of static friction, which is directed radially towards the center of the path.
- 🌀 The velocity of the coin in circular motion can be calculated using the formula V = 2πR/T, where R is the radius and T is the period.
- ⏱️ The period (T) is defined as the time for one complete cycle of motion or one revolution around the circle.
- 📊 To reduce experimental error, the student can conduct multiple trials and use a motion sensor to accurately detect the moment the coin slips.
- 🔧 Newton's second law is applied to set up the equation for the period, focusing on the horizontal direction and the force of friction.
- 📈 A graph of T² (period squared) versus R² (radius squared) is plotted, and the slope of the best-fit line is used to calculate the coefficient of static friction (μs).
- 🔢 The slope of the graph represents the value of (4π²R)/μG, and by rearranging the equation, the value of μs can be solved.
- 🧠 Understanding the relationship between T² and R² is crucial for correctly interpreting the graph and calculating the coefficient of static friction.
- 🎓 The problem requires a solid grasp of circular motion concepts and the ability to apply them to real-world scenarios, such as the one presented in the transcript.
Q & A
What is the main objective of the experiment described in the transcript?
-The main objective of the experiment is to determine the coefficient of static friction (μs) between a coin and a steel plate using principles of circular motion and gravitation.
What are the key pieces of equipment used in the experiment?
-The key pieces of equipment used in the experiment include a steel plate attached to a freely rotating axis, a coin, a method to measure the distance R from the center of rotation to the coin, and a stopwatch to measure the period T of the plate's rotation.
How does the student determine the point at which the coin slips off the plate?
-The student starts by rotating the plate slowly and gradually increases the speed. The point at which the coin slips off the plate is determined by the speed of rotation at that moment.
Why is it important to record the rotational speed when the coin slips off the plate?
-Recording the rotational speed when the coin slips off is important because this speed corresponds to the maximum static friction that can be provided between the coin and the plate, which is necessary for calculating the coefficient of static friction.
What is the significance of the period (T) in this experiment?
-The period (T) is the time it takes for one complete cycle of motion or one full revolution around the plate. It is crucial for calculating the velocity of the coin in its circular motion and subsequently determining the centripetal force required to keep the coin in motion.
How can experimental error be reduced in measuring the moment the coin slips off?
-Experimental error can be reduced by using an electronic motion sensor to detect the exact moment the coin slips off, instead of relying on a stopwatch, which can introduce human reaction time errors.
What is the role of static friction in this experiment?
-Static friction provides the centripetal force that keeps the coin in circular motion on the steel plate. The maximum static friction force is what allows the coin to stay on the plate up to the point it slips off.
What is the formula derived from Newton's second law for this experiment?
-The formula derived from Newton's second law is mu * m * g = m * (V^2) / R, where mu is the coefficient of static friction, m is the mass of the coin, g is the acceleration due to gravity, V is the velocity of the coin, and R is the radius of the circular path.
How is the coefficient of static friction (μ) calculated in the end?
-The coefficient of static friction (μ) is calculated by rearranging the derived formula and solving for μ, which gives μ = (4 * π^2 * R^2) / (T^2 * g). The slope of a graph plotting T^2 versus R^2 is used to find the value of μ.
What is the importance of conducting multiple trials in this experiment?
-Conducting multiple trials helps to reduce random errors and increase the reliability of the results by averaging out any anomalies that may occur in individual trials.
How does the experiment relate to real-world scenarios?
-The experiment simulates scenarios like a car sliding on a road where static friction is the force that provides the necessary centripetal force to keep the car in circular motion while turning.
Outlines
📚 Introduction to AP Physics Workbook - Circular Motion and Gravitation
This paragraph introduces the AP Physics workbook focusing on Unit Three, which deals with circular motion and gravitation. The specific section, 3.K, is about friction as an internal force. The scenario involves a student who is trying to determine the coefficient of static friction (mus) between a coin and a steel plate. The student sets up the steel plate with the center attached to a freely rotating axis and places the coin at different positions on the plate. The student measures the distance (R) from the center to the coin and uses a stopwatch to measure the period (t) of the plate's rotation. The goal is to explain how the student can set up the experiment to take measurements that will allow the calculation of the coefficient of friction.
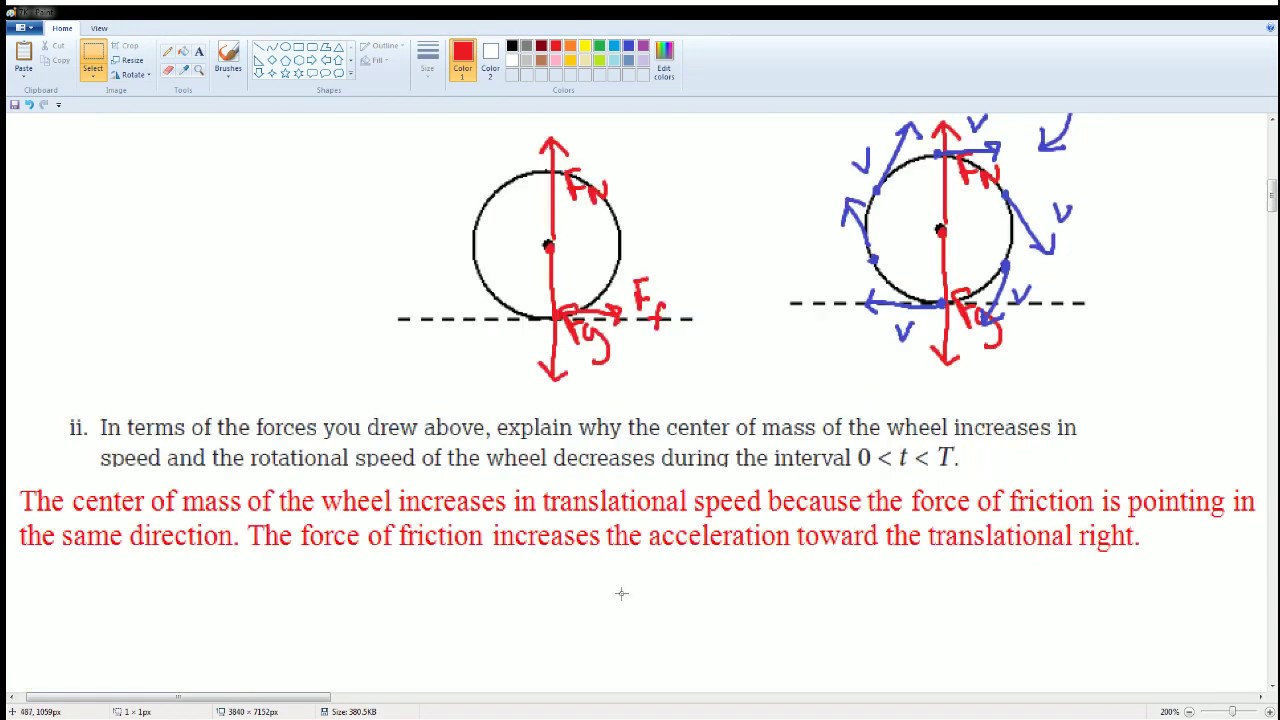
🔍 Understanding the Static Friction and Centripetal Force
In this paragraph, the focus is on understanding the role of static friction as a centripetal force that keeps the coin in circular motion. The static friction force is directed radially towards the center of the circular path, calculated as MV^2/R, which is equal to the maximum static friction (mu times the normal force). The student is advised to start with a slow rotation and gradually increase the speed until the coin slips off the plate. The speed at which the coin slips off is crucial and must be recorded, as well as the rotational period. The period (T) is defined as the time for one complete cycle or revolution. To minimize experimental error, the student can conduct multiple trials or use a motion sensor to detect the moment the coin slips.
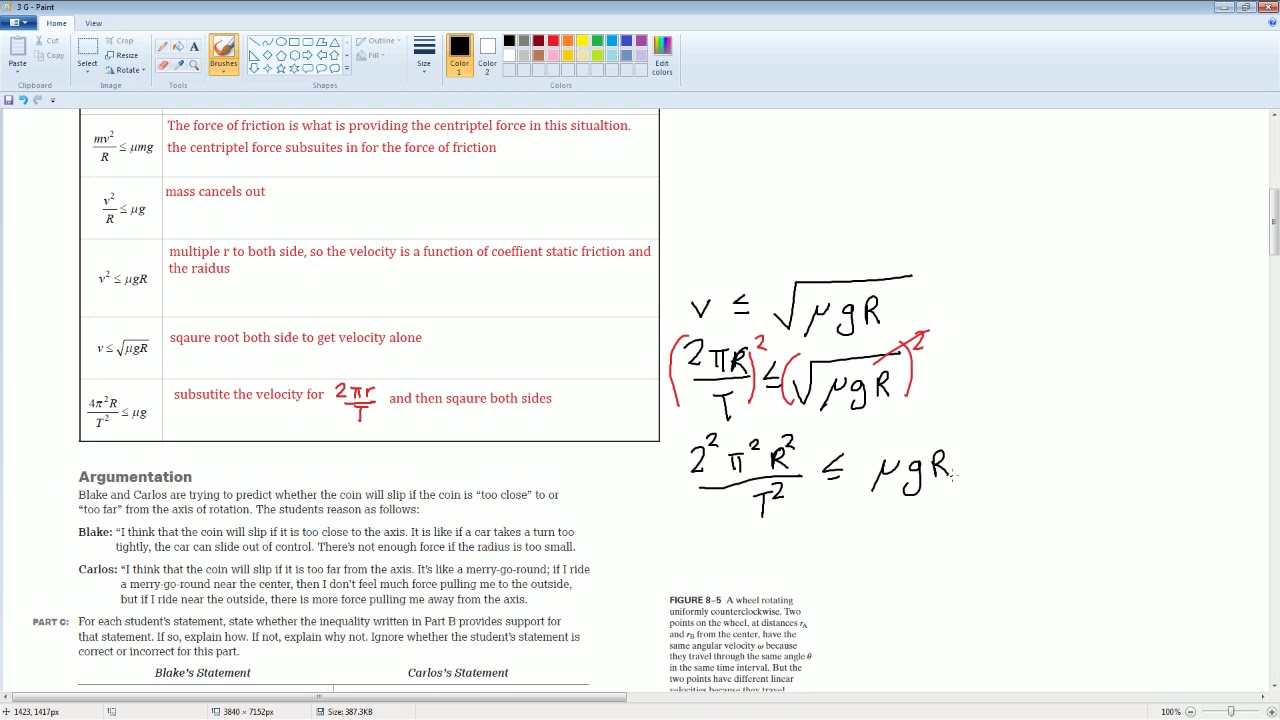
📝 Deriving the Equation for Period and Velocity
This paragraph delves into the derivation of the equation for the period (T) using Newton's second law of motion. The force of friction is what provides the necessary centripetal force. The equation is set up with the friction force (mu times the normal force, represented as mg) being equal to the mass times the velocity squared over R (MV^2/R). By canceling out the mass, the equation simplifies to ugR = V^2 / (2πR). The velocity (V) is then expressed as 2πR/T. Substituting this back into the equation and performing algebraic manipulations, the period squared (T^2) is related to the radius (R) and gravitational force (G), leading to the equation T^2 = (4π^2R^3)/(muG). The student is then guided to plot a graph of T^2 versus R^2, find the best line fit, and calculate the slope to determine the value of mu.
🧮 Calculating the Slope and the Coefficient of Static Friction
The paragraph explains the process of calculating the slope from the graph of T^2 versus R^2 and using it to find the coefficient of static friction (mu). The slope represents the ratio of the change in period squared (ΔT^2) to the change in radius (ΔR). The equation derived earlier is rearranged to solve for mu, resulting in muG = (4πR * T^2) / R^2. After calculating the slope using the given data points and performing the necessary algebraic steps, the value of mu is computed by multiplying the slope by the constant (4π^2R^3/G). The final value of mu is given as approximately 0.24, emphasizing the importance of rounding to a reasonable number of significant digits in physics.
🎓 Correcting the Slope Calculation and Finalizing the Coefficient of Static Friction
The final paragraph corrects a mistake made in the previous calculation regarding the slope interpretation. It clarifies that the slope actually represents T^2 / R, not R / T^2 as previously stated. The correct equation for the slope is T^2 / R, which is found to be 16. The calculation is then revised accordingly, with the slope being the reciprocal of the corrected equation. The final value of the coefficient of static friction (mu) is recalculated using the correct formula and the previously determined slope, resulting in a value of approximately 0.24. The paragraph concludes by emphasizing the importance of understanding the correct relationships and formulas when solving physics problems.
Mindmap
Keywords
💡Circular Motion
💡Gravitation
💡Coefficient of Static Friction
💡Centripetal Force
💡Velocity
💡Period
💡Normal Force
💡Newton's Second Law
💡Rotational Period
💡Friction
💡Data Analysis
Highlights
The scenario involves a student determining the coefficient of static friction (mus) between a coin and a steel plate.
The student attaches the center of the plate to a fixed, freely rotating axis and sets the coin on different positions on the steel plate.
The distance R from the center to the coin and the center of rotation is measured, along with the period (t) of the plate rotation using a stopwatch.
Friction acts as an internal force in this experiment, providing the centripetal force necessary to keep the coin in circular motion.
The velocity of the coin in circular motion is calculated using the formula MV^2/R, which is equal to the maximum static friction (mu times the normal force).
The student gradually increases the speed of rotation until the coin slips off the plate, recording the speed and rotational period at that point.
The period (T) is defined as the time for one cycle of simple harmonic motion or one full wavelength passing a certain position.
To reduce experimental error, multiple trials can be conducted, and a motion sensor can be used to detect the exact moment the coin slips.
Newton's second law is applied to set up the equation for the period of rotation, focusing on the horizontal direction and the force of friction.
The equation derived from Newton's law and basic principles leads to T^2 being directly proportional to R, allowing for the calculation of the coefficient of friction (mu).
A graph of T^2 versus R^2 is plotted, and the slope of the best-fit line is used to calculate mu.
The value of mu is calculated using the slope from the graph and the equation 4PI^2R^2/muG, where G is the acceleration due to gravity.
The final calculated value for mu is approximately 0.24, which is unitless and represents the coefficient of static friction.
This problem combines concepts of circular motion and simple harmonic motion to provide a comprehensive understanding of frictional forces in physics.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: