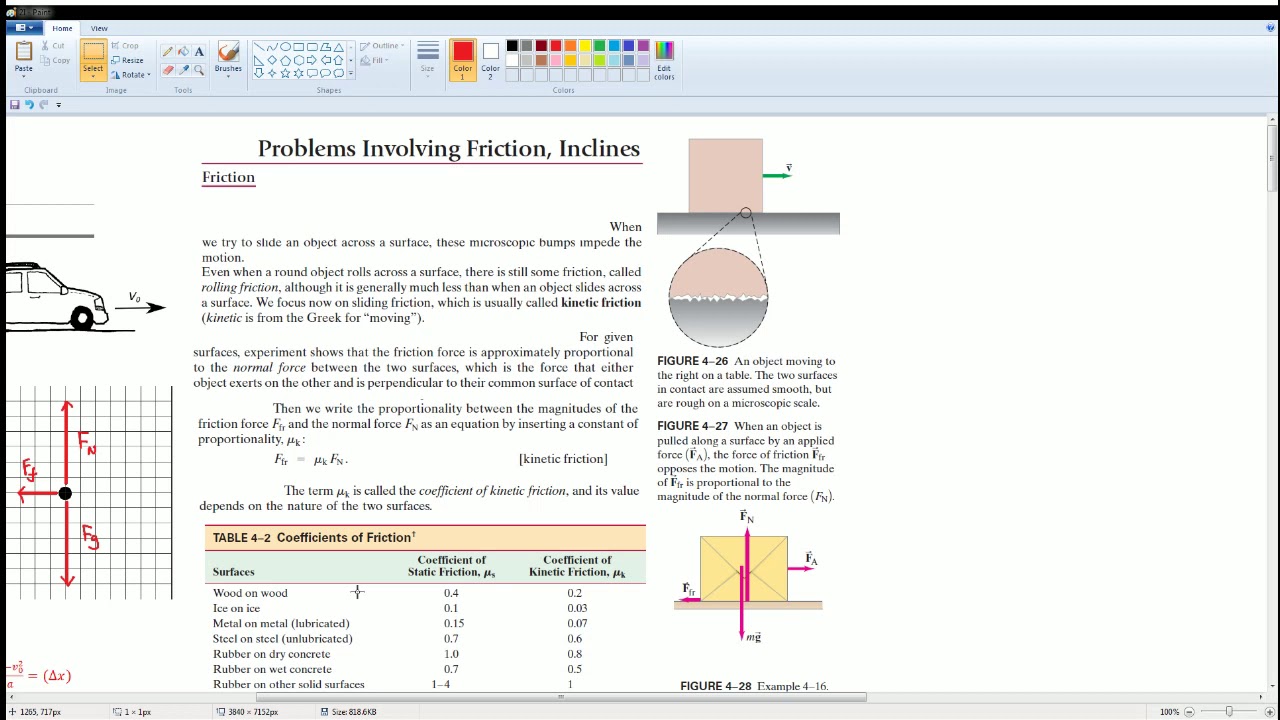
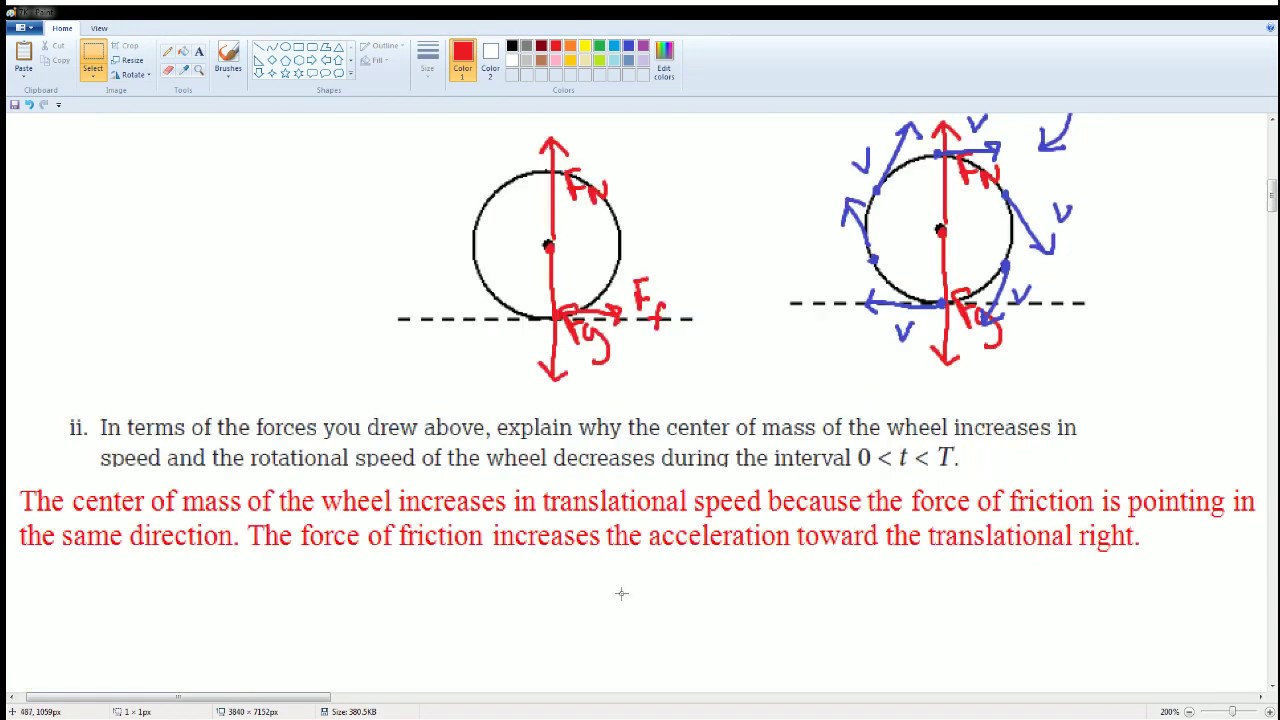
AP Physics Workbook 3.G Mass and Frictional Force
TLDRThe video script discusses the physics concepts of circular motion and gravitation, focusing on the conditions under which a coin on a rotating surface will slip due to insufficient static friction. It explains the role of the coefficient of static friction, mass, and radius in determining the likelihood of the coin slipping. The key equation derived relates velocity, friction, and gravitational force, showing that the mass of the coin does not affect the slipping threshold, as it is canceled out in the formula. The explanation helps clarify the physical principles at play and the factors influencing the stability of an object in circular motion.
Takeaways
- 📚 The scenario involves a coin of mass M on a rotating surface at a distance R from the axis of rotation.
- 🔄 The surface rotates with a certain angular velocity, and the coin's position on the surface affects whether it stays in place or slips.
- 🚫 The force of static friction is what prevents the coin from slipping and provides the necessary centripetal force for circular motion.
- 🎯 The maximum static friction force is given by the product of the coefficient of static friction (μ) and the normal force (mg).
- 🌐 The velocity of the coin is related to the coefficient of static friction, the radius of rotation, and gravitational force (mv²/R = μmg).
- 🔢 The mass of the coin (M) cancels out in the equation for velocity, indicating that mass does not affect the likelihood of the coin slipping.
- 📉 As the radius (R) increases, the likelihood of the coin slipping also increases because the gravitational pull is less effective at larger distances.
- 📈 Conversely, when the coin is closer to the axis of rotation (smaller R), it is less likely to slip due to the stronger gravitational pull.
- 🤔 The students' debate about the effect of the coin's mass on slipping is resolved by the fact that the equation for velocity does not include mass.
- 🌌 The principles discussed can be applied to understand celestial bodies' motion, such as the moon's orbit around Earth.
Q & A
What is the main topic of the video?
-The main topic of the video is the study of circular motion and gravitation, specifically focusing on the conditions under which a coin placed on a rotating surface will slip due to mass and friction.
What is the significance of the mass of the coin in relation to static friction?
-The mass of the coin does not affect the likelihood of slipping because it cancels out in the equation that relates static friction, velocity, and radius. The force of friction depends on the coefficient of static friction, velocity, and radius, not the mass.
How does the distance (R) of the coin from the axis of rotation affect the possibility of slipping?
-The distance (R) from the axis of rotation affects the possibility of slipping because as R increases, the left side of the friction equation increases. If R is too large, the friction force may not be enough to keep the coin in circular motion, leading to slipping.
What is the role of the coefficient of static friction (mu) in the scenario?
-The coefficient of static friction (mu) is crucial as it defines the maximum possible force of friction the surface can exert to keep the coin in place. It is part of the inequality that determines whether the coin will slip or not.
What happens when the force of friction is equal to the centripetal force required for circular motion?
-When the force of friction is equal to the centripetal force, the coin is able to maintain its circular motion without slipping. The friction force is providing the necessary centripetal force to keep the coin in motion around the axis of rotation.
How does the gravitational force (mg) factor into the equation?
-The gravitational force (mg) is part of the normal force that acts on the coin. It is considered when calculating the maximum static friction force, which is mu times the normal force (FN = m(g) in this case).
What is the significance of the inequality derived in the video?
-The derived inequality (f_friction ≤ mu * FN) must be satisfied for the coin to remain in place on the rotating surface. If the inequality is not met, the coin will slip because the friction force is insufficient to provide the necessary centripetal force.
What is the relationship between the velocity (v) of the coin and the radius (R) of the circle?
-The velocity (v) of the coin is directly related to the radius (R) of the circle by the equation v = sqrt(mu * g * R). As R increases, the velocity also increases, assuming mu and g remain constant.
Why does the video mention that the coin is less likely to slip when it is closer to the axis of rotation?
-When the coin is closer to the axis of rotation, the radius (R) is smaller, which results in a smaller value for the friction force required to keep the coin in motion. This makes it less likely to slip because the gravitational pull (mu * g) acting on the coin is more effective at preventing it from moving away from the center.
How does the video explain the concept of gravitational pull in relation to the coin's position on the rotating surface?
-The video explains that the gravitational pull, represented by mu * g, is what keeps the coin in circular motion. The closer the coin is to the center, the stronger the gravitational pull, making it less likely to slip. Conversely, the further away the coin is from the center, the weaker the gravitational pull, increasing the likelihood of slipping.
What is the final conclusion regarding the coin's likelihood of slipping based on the video's analysis?
-The final conclusion is that the coin is more likely to slip when it is far away from the axis of rotation because the gravitational pull (mu * g) is weaker at larger radii, making it less effective at preventing the coin from slipping out of its circular path.
Outlines
📚 Introduction to Circular Motion and Gravitation
This paragraph introduces the topic of circular motion and gravitation from the AP Physics workbook. It sets the scenario of a coin with mass M placed on a rotating surface at a distance R from the axis of rotation. The surface's rotation causes certain locations on it where the coin can be placed based on the force of static friction. The coefficient of static friction between the coin and the surface is represented by mu. The paragraph discusses the conditions under which the coin will not slip due to insufficient static friction. It also introduces the concept of centripetal force, which is provided by the force of friction in this context, and explains how to represent these forces in a free-body diagram.
🔄 Centripetal Force and Static Friction
In this paragraph, the concept of centripetal force is further explored, emphasizing its substitution for the force of friction. The equation MV^2/R is derived, showing that the force of friction becomes MV^2/R in the given situation. It is explained that the mass cancels out, leading to a relationship between velocity, coefficient of static friction, and radius. The derivation of the inequality is detailed, highlighting how the velocity is a function of these variables. The paragraph also clarifies the mathematical steps involved in deriving the final expression for velocity in terms of the coefficient of static friction, gravitational force, and radius.
🌐 Effect of Distance from Axis of Rotation
This paragraph examines the effect of the distance (radius) from the axis of rotation on the likelihood of the coin slipping. It explains that when the coin is closer to the axis of rotation, the gravitational pull is stronger, reducing the likelihood of slipping. Conversely, when the coin is farther from the axis, it experiences less gravitational pull, increasing the chances of slipping. The paragraph uses physical principles and mathematical equations to illustrate why objects closer to the center of rotation are more firmly held in place, while those further away are more likely to escape the gravitational pull.
💫 Gravitational Pull and Coin's Slippage
The discussion continues with an exploration of the gravitational pull's influence on the coin's tendency to slip. It is explained that the gravitational strength decreases as one moves away from the center, which affects the coin's likelihood of slipping. The paragraph clarifies the misconceptions about the forces acting on an object in a rotating scenario, emphasizing that there is no centrifugal force acting outward. Instead, it is the gravitational pull that keeps the object in orbit, and this pull is weaker at greater distances from the center of rotation.
🔢 Mass of Coin and Slippage
The final paragraph addresses the debate between Angelica and Domenic regarding the mass of the coin and its likelihood of slipping. Using the derived equation and physical principles, it is concluded that the mass of the coin does not affect whether it will slip or not. The equation shows that the force of friction, which is critical in preventing slippage, is dependent on the radius and the coefficient of static friction, but not on the mass of the coin. This conclusion is based on the fact that the mass term cancels out in the relevant equations, indicating that the gravitational pull and frictional force acting on the coin are independent of its mass.
Mindmap
Keywords
💡Circular Motion
💡Gravitation
💡Mass
💡Friction
💡Coefficient of Static Friction
💡Centripetal Force
💡Rotating Surface
💡Velocity
💡Radius
💡Free Body Diagram
💡Inequality
Highlights
Circular motion and gravitation are discussed in Unit 3 of the AP Physics workbook.
The scenario involves a coin of mass M on a rotating surface at a distance R from the axis of rotation.
The force of static friction determines whether the coin spins with the surface or slips.
The coefficient of static friction between the coin and the surface is denoted by mu.
Free body diagram of the coin shows three forces acting on it: gravitational force, normal force, and frictional force.
The inequality derived from the deviation notes the conditions under which the coin does not slip on the surface.
The force of static friction is less than or equal to the coefficient of static friction times the normal force.
The normal force is equal to the mass times the gravitational acceleration (mg).
The force of friction provides the centripetal force necessary for circular motion.
The velocity of the coin is a function of the coefficient of friction, the radius, and the gravitational acceleration.
The equation for the maximum velocity before the coin slips is derived and explained.
The likelihood of the coin slipping is discussed in relation to its distance from the axis of rotation.
A coin is less likely to slip if it is closer to the axis of rotation due to a stronger gravitational pull.
The coin is more likely to slip if it is farther from the axis of rotation due to a weaker gravitational pull.
The mass of the coin does not affect whether it slips or not, as it cancels out in the relevant equations.
The discussion involves comparing the gravitational pull and the frictional force to determine the coin's motion.
The coin's mass is not a factor in the likelihood of slipping, as the equation is independent of mass.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: