AP Physics 1 Workbook 1.O 2D Motion Solution

Mr.S ClassRoom
31 Mar 202020:01
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the physics problem of calculating the speed of a dart launched from a crossbow. It explains the scenario where an engineer tests a new crossbow design by measuring the speed of the dart at the moment of launch. The crossbow is fixed horizontally, and the dart's trajectory, affected by gravity, is analyzed. The video derives an equation for the time of flight (T) based on the height (H) the dart drops and the acceleration due to gravity (G). It then uses this equation to fill in a table and graph the relationship between horizontal distance and time. Finally, it calculates the crossbow's launch speed by determining the slope of a distance versus time graph. The video emphasizes the importance of understanding the concepts and applying the correct mathematical equations to solve physics problems.

Takeaways
  • 🎯 The problem involves an engineer testing a new crossbow design to determine the speed of a dart at the moment of launch.
  • 🏹 The crossbow is mounted on a table, shooting darts horizontally at a target placed at varying distances.
  • πŸ“ The dart's trajectory is affected by gravity, causing it to drop a distance H as it travels.
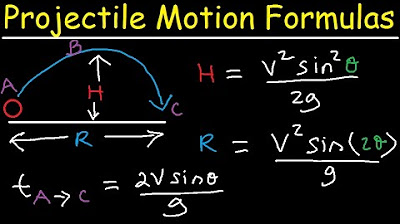
  • πŸ“ˆ The key equation derived to calculate the time of flight (T) is T = √(2H/G), where H is the height drop and G is the acceleration due to gravity.
  • πŸ“Š The problem requires filling a table with calculated times using the derived equation for different given heights.
  • πŸ€” The motion of the dart is parabolic, and understanding this trajectory is crucial for accurate calculations.
  • πŸ“‰ The video emphasizes the importance of graphing the data correctly, with time on the x-axis and horizontal distance on the y-axis.
  • πŸ“Œ A well-constructed graph should cover the entire range of values for both time and horizontal distance.
  • πŸ”’ The slope of the line in the distance versus time graph represents the speed at which the crossbow launches the dart.
  • πŸ“ The average speed is calculated by finding the slope between two points on the graph, using the formula Ξ”X/Ξ”Y.
  • πŸ’‘ The video stresses the importance of using a reasonable number of significant digits in calculations, as per AP test standards.
Q & A

  • What is the main scenario described in the transcript?

    -The main scenario involves an engineer testing a new crossbow design to determine the speed of a dart when it is launched horizontally from the crossbow, which is fixed to a table.

  • How is the target set up in relation to the crossbow?

    -The target is placed directly in front of the crossbow, with the crossbow pointed at the center of the target. The distance from the crossbow to the target is varied, and the horizontal distance (D) is measured as well as the distance (H) the dart strikes the target from the center.

  • What is the expected trajectory of the dart according to the script?

    -The expected trajectory of the dart is a parabolic path due to the influence of gravity, with the dart falling a distance H below the horizontal line from the crossbow to the target.

  • What is the fundamental equation used to derive the time of flight (T) for the dart?

    -The fundamental equation used is the one that relates the distance fallen (H) to the square of the time of flight (T), with the acceleration due to gravity (g), which is H = (1/2) * g * T^2.

  • How is the time of flight (T) calculated for the dart?

    -The time of flight (T) is calculated using the formula T = √(2H/g), where H is the distance the dart falls and g is the acceleration due to gravity.

  • What is the significance of the derived equation for the time of flight?

    -The derived equation for the time of flight is significant because it is a universal equation that can be used to calculate the time for any object undergoing parabolic motion, specifically for horizontal projectile motion.

  • How does the script describe the process of graphing the motion of the dart?

    -The script describes the process of graphing the motion of the dart by setting up a line of best fit. The vertical axis represents the horizontal distance (D), and the horizontal axis represents the time (T). The graph should cover the entire range of values for both axes, with time on the horizontal axis and the horizontal distance of the target on the vertical axis.

  • What is the purpose of graphing the motion of the dart?

    -The purpose of graphing the motion of the dart is to visually analyze the relationship between the horizontal distance and the time of flight, which can help in understanding the projectile motion and in determining the speed at which the crossbow launches the dart.

  • How is the speed of the crossbow-launched dart determined from the graph?

    -The speed of the crossbow-launched dart is determined from the graph by finding the slope of the line of best fit. The slope represents the instantaneous speed of the dart at the point where it is launched.

  • What is the importance of understanding significant digits in the context of the AP Physics exam?

    -Understanding significant digits is important in the context of the AP Physics exam because while the rule for significant digits is not directly tested, students are expected to use a reasonable number of significant digits in their calculations. This ensures the quality of the measurements and the accuracy of the results, as points may be deducted for an unreasonable number of significant digits.

  • How does the script emphasize the importance of the derived equation and graphing in solving the problem?

    -The script emphasizes the importance of the derived equation and graphing by showing that these tools are crucial for solving the problem. The equation allows for the calculation of the time of flight and understanding the projectile motion, while graphing helps visualize the relationship between the variables and derive the speed of the dart. These methods are essential for analyzing and solving problems in physics.

Outlines
00:00
🏹 Introduction to 2D Motion and Crossbow Design

This paragraph introduces the AP Physics workbook and the specific section on 2D motion. The scenario involves an engineer testing a new crossbow design to determine the speed of a dart at the moment of launch. The crossbow is fixed to a table, ensuring horizontal launch, with a target placed at varying distances. The challenge is to measure the horizontal distance (D) and the height (H) the dart drops from the center of the target upon impact. The discussion highlights the parabolic trajectory of the dart due to gravity and the goal of calculating the time it takes for the dart to hit the target using fundamental physics equations.

05:03
πŸ“š Deriving the Equation for Time of Flight

The second paragraph delves into the derivation of the equation for the time (T) it takes for the dart to hit the target. The focus is on using the correct fundamental equation from the formula sheet, considering the dart's horizontal projection and the effect of gravity on its vertical descent. The equation involves the height (H) the dart drops and the acceleration due to gravity (g). Through a step-by-step process, the paragraph explains how to arrive at the equation T = √(2H/g) and emphasizes the importance of understanding the relationship between the variables and the application of this equation for calculating the time of flight in similar horizontal projectile motion scenarios.

10:09
πŸ“ˆ Graphing the Motion and Understanding Scale

This paragraph discusses the process of graphing the motion of the dart to understand the relationship between horizontal distance (D) and time (T). It emphasizes the importance of proper scaling and the selection of appropriate axes for the graph. The discussion includes the creation of a line of best fit and the interpretation of the graph in terms of the dart's motion. The paragraph also provides guidance on how to avoid common mistakes in graphing, such as improper scaling and misinterpretation of the graph's range and domain.

15:10
πŸš€ Calculating the Crossbow's Launch Speed

The final paragraph focuses on using the derived equations and the graph to calculate the speed at which the crossbow launches the dart. It explains how to determine the slope of the distance versus time graph and how this slope represents the average speed of the dart. The paragraph also touches on the concept of significant figures and their importance in calculations, emphasizing the need for reasonable and acceptable numbers of significant figures in the context of the AP Physics exam.

Mindmap
Keywords
πŸ’‘2D Motion
2D Motion refers to the movement of an object in two dimensions, typically horizontal and vertical. In the context of the video, it is used to describe the trajectory of a dart launched from a crossbow, which moves horizontally and is affected by gravity in the vertical direction. The analysis of 2D motion is crucial for understanding the path (trajectory) of the dart and calculating the time it takes to hit the target.
πŸ’‘Crossbow
A crossbow is a ranged weapon that uses an elastic launching mechanism similar to a bow and is designed to shoot projectiles called darts or bolts. In the video, an engineer is testing a new crossbow design to determine the speed of the dart at the moment it is launched. The crossbow is fixed to a table to ensure horizontal launching of the darts.
πŸ’‘Instantaneous Speed
Instantaneous speed is the speed of an object at a particular moment in time. It is different from average speed, which is calculated over a period of time or a certain distance. In the video, the instantaneous speed of the dart as it is launched from the crossbow is of interest, and the time it takes for the dart to hit the target is calculated to eventually determine this speed.
πŸ’‘Trajectory
Trajectory refers to the path that a moving object follows through space as it is acted upon by various forces. In the context of the video, the trajectory of the dart is parabolic due to the influence of gravity, which causes the dart to follow a curved path as it moves horizontally from the crossbow to the target.
πŸ’‘Gravity
Gravity is the force that attracts two bodies toward each other, the most common example being the Earth's gravitational pull on objects. In the video, gravity affects the dart's motion in the vertical direction, causing it to drop as it travels horizontally towards the target.
πŸ’‘Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. It is a vector quantity that describes how quickly an object speeds up, slows down, or changes direction. In the video, the term is used to describe the constant acceleration due to gravity acting on the dart in the vertical direction.
πŸ’‘Time of Flight
Time of flight refers to the total time taken by an object to travel from its point of origin to its target or destination. In the video, the time of flight is the time it takes for the dart to travel from the crossbow to the point where it hits the target.
πŸ’‘Horizontal Distance
Horizontal distance is the length of the path traveled by an object in a straight line, horizontally. In the video, the horizontal distance is the length between the crossbow and the target.
πŸ’‘Parabola
A parabola is a U-shaped curve that follows a quadratic equation. It is used in the study of projectile motion to describe the path of an object that is launched into the air and is affected only by gravity. In the video, the dart's trajectory through the air isθΏ‘δΌΌ (approximated) as a parabolic curve due to the influence of gravity.
πŸ’‘Deviation
Deviation refers to the difference or displacement from a specified or desired course, position, or value. In the context of the video, deviation is used to describe the vertical distance the dart drops from its initial position due to gravity, which causes it to deviate from a perfectly horizontal path.
πŸ’‘Significant Digits
Significant digits are the digits in a number that carry meaning contributing to its precision. This includes all digits except leading zeros, trailing zeros when they serve only as placeholders, and any digits that are merely placeholders to indicate the scale of the number. In the video, the concept is important when reporting measurements and calculations to ensure accuracy and precision.
Highlights

The scenario involves an engineer testing a new crossbow design to find the speed of a dart at the moment of launch.

The crossbow is fixed to a table, ensuring the dart is launched horizontally.

A target is placed at varying distances (D) from the crossbow, with the crossbow aimed directly at the center.

The dart's trajectory is affected by gravity, causing it to drop a distance (H) when it strikes the target.

The fundamental equation used to derive the time (T) of the dart's flight is based on the object's acceleration and time.

The equation H = (1/2)gT^2 is derived to calculate the time it takes for the dart to hit the target.

The time (T) can be calculated using the formula T = √(2H/g).

The video demonstrates how to fill in a table using the derived equation for different values of H.

The motion graph helps to understand the relationship between horizontal distance (D) and time (T).

The graph should have time on the x-axis and horizontal distance on the y-axis to represent the dart's trajectory.

The graph should cover the entire range of values to avoid an incomplete representation of the data.

The speed of the crossbow-launched dart can be determined by calculating the slope of the distance versus time graph.

The average speed is calculated by finding the slope between two points on the graph.

The significance of digits in calculations is crucial and should be based on the quality of measurement.

The video emphasizes the importance of understanding both the theoretical and practical aspects of the problem.

The process of deriving equations, plugging in values, and graphing are essential steps in solving the problem.

The video provides a comprehensive walkthrough of the problem, from setup to calculation to graphing.

Transcripts

Browse More Related Video

Distance Speed Time Word Problem Time to Overtake

Introduction to Projectile Motion - Formulas and Equations

Projectile Motion Time of Flight Formula Derivation

Solving Projectile Motion Problems in Physics - [1-4-7]

Science 10 physics: rearrange basic formulas

Speed, distance and time

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Projectile MotionPhysics ExperimentCrossbow DartCalculations2D MotionEngineeringAP PhysicsTrajectory AnalysisSpeed CalculationParabolic Trajectory