Centripetal force problem solving | Centripetal force and gravitation | Physics | Khan Academy
TLDRThis educational video demystifies common misconceptions about centripetal force, offering a deep dive into solving problems related to centripetal motion. It begins with a basic example of a ball rotating in a circle due to the tension in a string, emphasizing that centripetal force is not a new type of force but rather a directional property of forces we are already familiar with. Through step-by-step examples, including a ball on a string and a bike riding over a circular hill, the instructor provides practical strategies for solving centripetal force problems using Newton's second law, illustrating the importance of recognizing the direction of forces and correctly identifying the forces at play. The video aims to strengthen problem-solving skills in physics by clarifying the concept of centripetal force and demonstrating its application in various scenarios.
Takeaways
- 🔄 Centripetal force is not a new or unique force, but one of the known forces (like tension or gravity) directed toward the center of a circle.
- 🎢 In circular motion problems, identifying the actual force acting as the centripetal force (e.g., tension in the rope) is crucial for accurate analysis.
- 🔍 The common misconception is that there are separate forces for tension and centripetal force, when in reality they are the same if the tension is directed toward the center.
- 📏 Problem-solving in centripetal force scenarios involves the same steps as in other force problems: drawing a force diagram and applying Newton's second law.
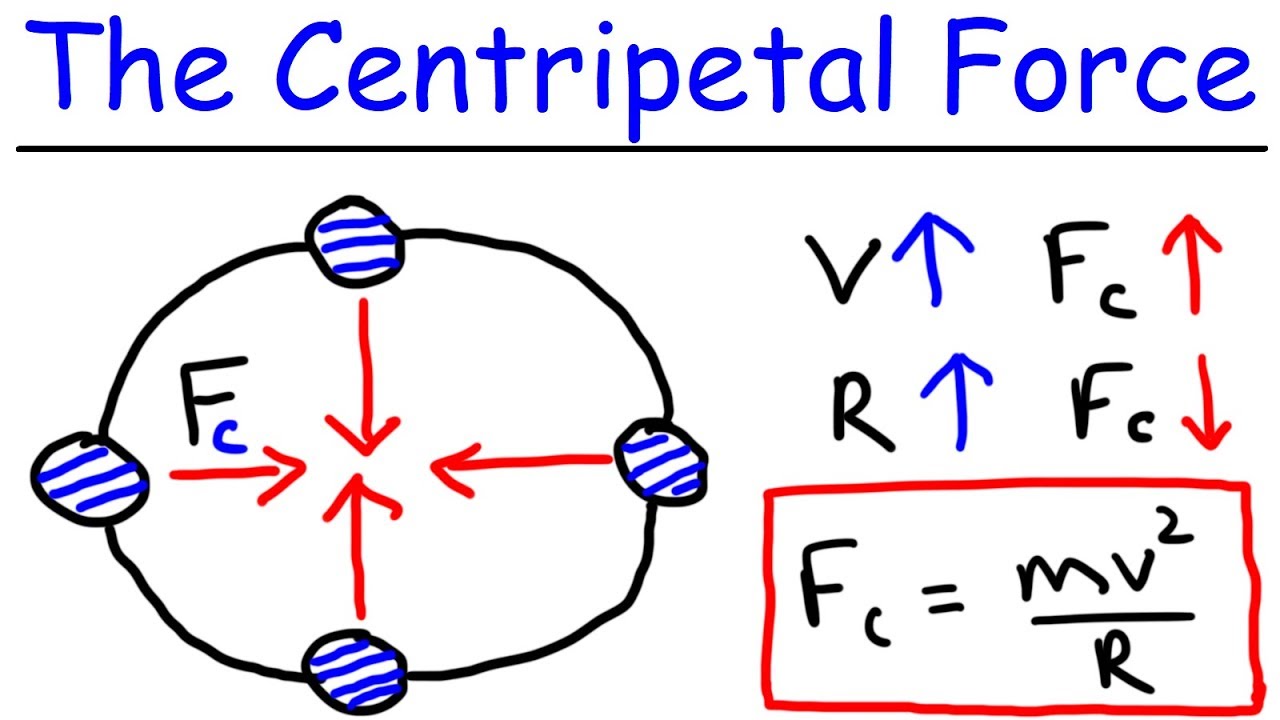
- 🔄 Centripetal acceleration is used in calculations and is defined as v^2 / r, where v is velocity and r is the radius of the circular path.
- 🔑 Only forces directed toward or away from the center of the circle are considered in centripetal force problems; other forces are irrelevant in this context.
- ⚖️ Misinterpretation of forces can lead to incorrect conclusions, such as confusing the centripetal force with other forces like normal or gravitational forces.
- 🚴 When analyzing motion over a curved path (like a hill), the normal force can be less than the gravitational force, leading to a sensation of weightlessness.
- 💡 Understanding the direction of forces in circular motion is key; forces pointing toward the center are positive, and those pointing outward are negative in centripetal calculations.
- 📚 Thorough problem-solving strategy and understanding of physics concepts are essential to correctly solve and understand centripetal force problems.
Q & A
What is a common misconception about centripetal force?
-A common misconception is that centripetal force is a new kind of force. In reality, it's just one of the known forces (like tension, gravity, normal force, or friction) that happens to point toward the center of a circle, causing an object to move in a circular path.
In the provided ball and string example, what kind of force acts as the centripetal force?
-In the ball and string example, the tension in the string acts as the centripetal force, pulling the ball towards the center of the circle.
Why can't you consider centripetal force as an additional force apart from tension in the ball and string example?
-You can't consider centripetal force as an additional force apart from tension because the tension itself is the centripetal force. Representing it twice would be incorrect, similar to equating the upward force and normal force as two different entities when they are the same.
What is the secret to solving centripetal force problems?
-The secret to solving centripetal force problems is to approach them the same way as any other force problem: by drawing a force diagram and applying Newton's second law for each direction separately.
What forces should be included when calculating the net force in the direction of centripetal acceleration?
-Only forces that are directed radially toward or away from the center of the circle should be included when calculating the net force in the direction of centripetal acceleration. Forces directed inward are positive, and forces directed outward are negative.
What is a centrifugal force and is it considered a real force in physics?
-Centrifugal force is often thought to be a real force that acts outward on an object moving in a circle. However, in physics, it is considered a fictitious force that does not exist when using a proper reference frame. It's a perceived force due to inertia when an object wants to continue moving in a straight line.
How would you solve for the force of tension in the rope in the ball and string example?
-To solve for the force of tension in the rope, you use the formula T = m * v^2/r, where m is the mass of the ball, v is the velocity, and r is the radius of the circle. This calculation follows after establishing that tension is the centripetal force.
Why does a bike riding over a circular hill not maintain its height off the ground?
-As a bike rides over the crest of a circular hill, it does not maintain its height due to gravity pulling it downward, which is greater than the normal force at that moment. This causes the bike to accelerate downward and continue down the hill, rather than hovering off into space.
How do you calculate the normal force exerted on you and your bike as you ride over the crest of a hill?
-To calculate the normal force exerted as you ride over the crest of a hill, you can use the equation N = mg - m * v^2/r, where m is the mass of you and your bike, g is the acceleration due to gravity, v is your velocity, and r is the radius of the hill.
What does it imply if the normal force becomes zero when driving over a hill?
-If the normal force becomes zero when driving over a hill, it implies that you become airborne. This occurs when the outward centrifugal 'force' due to your velocity and the shape of the hill cancels out the inward gravitational pull, effectively making you weightless momentarily.
Outlines
🌀 Understanding Centripetal Force Misconceptions
This section begins with the instructor addressing common misconceptions about centripetal force in physics. Through an example of a ball tied to a string rotating on a frictionless table, the instructor illustrates the concept of centripetal force, emphasizing that it's not a unique type of force but rather any force directed towards the center of the circle. The force causing the ball to circle, in this case, is identified as tension in the string. This example serves to clarify that centripetal force is merely a directional characteristic of a force, not a separate force in itself, challenging the misconception that it is a novel force type. The instructor stresses the importance of accurately identifying the force acting as the centripetal force, using tension as an illustrative example, and warns against the common mistake of considering centripetal force as an additional, separate force.
🔍 Solving Centripetal Force Problems
In the second paragraph, the instructor delves into solving problems involving centripetal forces with a specific example involving the tension in the rope causing a ball to move in a circular motion. The key strategy highlighted for solving such problems is treating them like any other force problem: drawing a quality force diagram and applying Newton's second law. The focus is on selecting the correct direction for analysis, which, in the case of centripetal force problems, is radially into the circle (centripetal direction). The instructor clarifies a common error where learners mistakenly include all forces in the centripetal force calculation, emphasizing that only forces directed towards the center should be considered. The explanation culminates in solving for the tension in the rope, providing a clear example of how to approach and solve centripetal force problems correctly.
🚴 Overcoming Centripetal Force Challenges
The third section builds on the previous examples by introducing a new scenario where a bicyclist rides over a circular hill. This example is used to demonstrate the application of the principles discussed earlier in a different context. The instructor explains why the normal force experienced by the bicyclist and the bike at the crest of the hill cannot be equal to the gravitational force, debunking a common assumption. By applying Newton's second law in the vertical (centripetal) direction and carefully considering which forces to include in the calculation, the instructor solves for the normal force. This solution illustrates the experienced reduction in normal force (feeling of weightlessness) when moving over the hill at speed. This part reinforces the importance of a systematic approach to solving physics problems, specifically highlighting the need to correctly identify and calculate forces acting in the centripetal direction.
Mindmap
Keywords
💡Centripetal Force
💡Tension
💡Centripetal Acceleration
💡Newton's Second Law
💡Normal Force
💡Centrifugal Force
💡Inertia
💡Force Diagram
💡Velocity
💡Radius
Highlights
Common misconceptions about centripetal force are discussed, emphasizing that centripetal force is not a new type of force but rather the net force directed towards the center of the circular path.
The example of a ball tied to a string and rotating in a circle on a frictionless table is used to illustrate the concepts of centripetal force and motion.
The force causing the ball to move in a circular path is identified as the centripetal force, which is actually the tension from the string.
A detailed explanation of how to solve centripetal force problems using Newton's second law and a force diagram is provided.
The importance of identifying the correct forces to include in the centripetal force calculation is emphasized, with a clear distinction between forces pointing inward and outward.
A practical example of a bike riding over a circular hill is used to demonstrate how to apply the concepts of centripetal force and Newton's second law to real-world scenarios.
The concept of the normal force and its relationship to the centripetal force when an object is moving over a hill is explored.
The misconception of the existence of a centrifugal force is addressed, clarifying that it is not a real force but rather a perceived effect due to the inertia of the object.
The formula for centripetal acceleration, v^2/r, is introduced and used in the calculations to determine the force of tension in the rope.
The strategy for solving centripetal force problems is summarized, which involves drawing a force diagram and applying Newton's second law for the relevant direction.
The impact of speed on the normal force experienced when riding over a hill is discussed, highlighting the feeling of weightlessness at higher speeds.
The potential danger of becoming airborne when the normal force becomes zero due to excessive speed on a hill is warned against.
The importance of understanding the direction of forces and their role as positive or negative in the context of centripetal force calculations is stressed.
The relationship between the force of tension and the centripetal force is clarified, showing that the tension is the actual force acting as the centripetal force in the example given.
The calculation for the force of tension in the string is demonstrated, resulting in a force of 100 Newtons for the given example.
The concept of centripetal force is introduced as the net force directed towards the center of the circular motion, not as a separate or new type of force.
The example of riding a bike over a hill illustrates how the normal force can differ from the weight of the object due to the centripetal force.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: