AP Physics Workbook 3.D Vertical Circles
TLDRThe transcript discusses a physics problem involving a ball moving in a vertical circle, attached to a string. The conversation clarifies misconceptions about net force and centripetal force, emphasizing that centripetal force is the resultant of all forces, including tension and gravity. The problem involves calculating the minimum speed for the ball at the top of the circle without leaving the path and the subsequent motion of the ball if the string breaks, highlighting the principles of projectile motion and Newton's laws.
Takeaways
- 📚 The discussion revolves around a physics problem concerning a ball moving in a vertical circle, tied by a string and a rod.
- ✅ The net force on the ball at the top of the circle is not just the tension, as Dominic incorrectly assumed; it also includes the weight of the ball.
- 🔧 Carlos is partially correct in stating that the net force includes the typical tension and weight, but the term 'centripetal force' is not a standalone force; it's the resultant of all forces.
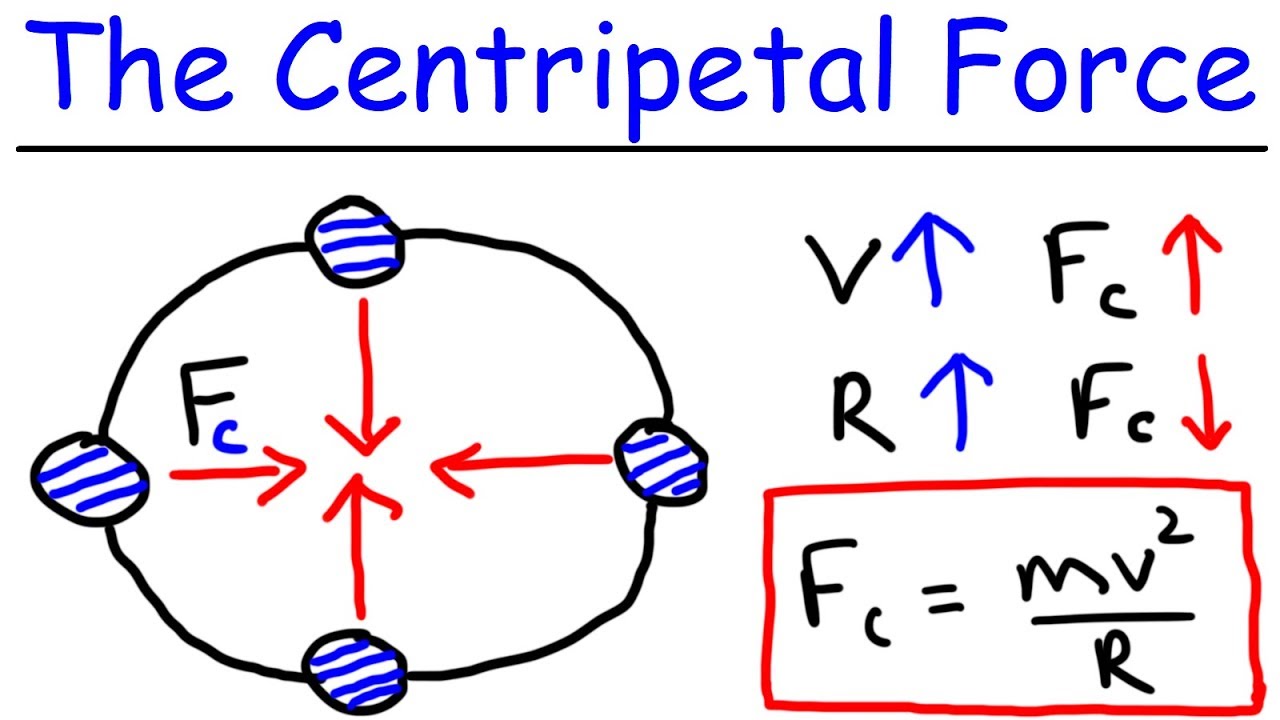
- 🎯 The concept of centripetal force is clarified as the net force required for an object to follow a circular path, which includes gravitational force, normal force, tension, and sometimes static friction.
- 🤹♂️ The problem-solving process involves analyzing the forces acting on the ball at different points in its circular path and summing them up to find the centripetal force.
- 📐 A free body diagram is used to visually represent the forces acting on the ball at each point, with the correct vector lengths and directions.
- 🌐 The direction of velocity and acceleration at any point in the circular path is tangential and towards the center, respectively.
- 🔄 When the string breaks, the ball's motion is described by projectile motion, with an initial upward velocity that decreases to zero at its maximum height before falling back down.
- 🚀 The velocity of the ball changes due to gravity's force, which is the only acceleration acting on it in the vertical direction.
- 📋 The mathematical expression for the minimum speed of the ball at the top of the circle (Point Z) is derived using Newton's second law and the formula for centripetal force.
Q & A
What is the topic being discussed in the transcript?
-The topic being discussed is the physics of vertical circles, specifically focusing on the forces acting on an object moving in a circular path and the minimum speed required for an object to maintain its circular motion without leaving the path.
What are the forces acting on the ball at the top of the circle according to the transcript?
-At the top of the circle, the forces acting on the ball are its weight (gravitational force) acting downwards and the tension in the cord acting upwards towards the center of the circle.
What is the correct statement regarding the net force on the ball at the top of the circle?
-The correct statement is that the net force on the ball at the top of the circle is the vector sum of the tension in the cord and the weight of the ball, both acting in the same direction downwards.
What is the significance of the centripetal force in the context of the transcript?
-The centripetal force is the net force acting on an object moving in a circular path, directed towards the center of the circle. It is not a new force but the resultant of all forces that cause the object to follow a circular path.
How does the tension in the cord affect the minimum speed of the ball?
-The tension in the cord is a force that contributes to the centripetal force required to keep the ball moving in a circular path. At the minimum speed, the tension in the cord is at its lowest value, and the only force preventing the ball from leaving the path is the gravitational force.
What is the formula used to calculate the minimum speed of an object in circular motion?
-The formula used to calculate the minimum speed (v) of an object in circular motion is v = sqrt(G * R), where G is the acceleration due to gravity and R is the radius of the circular path.
What happens to the ball when the string breaks while it is moving in a circular path?
-When the string breaks, the ball will fly off in the direction of its instantaneous velocity at the moment of the break, which is tangential to the circle at that point. It will then follow a projectile motion path, moving upwards to reach its maximum height before falling back down to the ground.
What is the acceleration of the ball after the string breaks?
-After the string breaks, the only acceleration acting on the ball is the acceleration due to gravity, which is 9.8 m/s^2 directed downwards towards the Earth.
What is the direction of the velocity of the ball at its maximum height after the string breaks?
-At its maximum height, the ball's velocity is zero because it momentarily stops moving upwards before it begins to fall back down.
How does the direction of the forces acting on the ball change as it moves around the circle?
-The direction of the forces acting on the ball changes as it moves around the circle. The gravitational force always points downwards, while the tension in the cord points towards the center of the circle. As the ball moves, these forces combine to create the centripetal force, which is directed inwards towards the center of the circle.
What is the significance of the free body diagram in understanding the problem?
-The free body diagram is a visual representation of all the forces acting on the ball at each point in its circular path. It helps to visualize and understand the vector sum of these forces, which is crucial for solving problems related to circular motion.
Outlines
📚 Physics Concepts and Student Arguments
This paragraph introduces the topic of vertical circular motion in AP Physics, focusing on unit three section three point D. The scenario involves a ball (BA) with a weight of two Newtons attached to a chord of length two meters. The tension in the cord is seven Newtons at the top and fifteen Newtons at the bottom. Two students, Dominic and Carlos, discuss the net force on the ball at the top of the circle. Dominic incorrectly assumes the net force is equal to the tension alone, while Carlos correctly identifies that the net force includes both tension and weight. The paragraph clarifies that centripetal force is the resultant of all forces acting towards the center, not a separate force, and that the internal force is a combination of gravitational, normal, tension, and sometimes static frictional forces.
📈 Visualizing Forces and Motion with Free Body Diagrams
This paragraph delves into the practical application of the physics concepts discussed earlier. It instructs on creating a free body diagram to visualize the forces acting on the ball at different points in its circular path. The paragraph emphasizes the importance of correctly labeling and sizing the vectors to represent the forces accurately. It also touches on the uniform motion of the ball in a clockwise direction and the resultant centripetal force, which is the inward force due to the combination of gravitational and tension forces at the top of the circle.
🧮 Mathematical Derivation of Minimum Speed
The paragraph focuses on the mathematical aspect of determining the minimum speed a ball can have at the top of a circular path without leaving it. It explains the derivation of the formula for minimum speed using the given formula sheet and the principles of physics. The explanation includes the substitution of variables and the process of solving for velocity, ultimately leading to the formula that relates gravitational force, velocity, and radius (G = V²/R). The paragraph also provides a practical example problem to illustrate the application of the derived formula.
🚀 Post-String-Break Motion Analysis
This paragraph discusses the motion of a ball after the string it was attached to suddenly breaks. It explains the direction the ball will fly based on the instantaneous velocity at the moment of the break, which is tangential to the circle. The paragraph uses Newton's first law to describe the ball's motion as a projectile, detailing the upward trajectory, reaching maximum height, and then falling back down to the ground. It also discusses the changes in velocity during this process, transitioning from positive to zero at the maximum height, and then to negative as the ball descends.
🔄 Centripetal Force and Projectile Motion
The final paragraph revisits the concepts of centripetal force and projectile motion. It corrects a minor mistake in a previous visual representation, emphasizing the importance of understanding the signs when dealing with the top and bottom of the circular path. The paragraph reinforces the basic vocabulary of centripetal force and provides a comprehensive overview of the physics principles discussed throughout the script.
Mindmap
Keywords
💡Vertical Circles
💡Centripetal Force
💡Tension
💡Gravitational Force
💡Net Force
💡Free Body Diagram
💡Acceleration
💡Projectile Motion
💡Newton's Laws of Motion
💡Minimum Speed
Highlights
The discussion revolves around the net force on a ball performing circular motion in a vertical plane.
Dominic incorrectly assumes that the net force on the ball at the top is equal to the tension in the cord.
Carlos correctly identifies that the net force includes both tension and weight, but mistakenly refers to it as 'some typical force'.
The correct understanding is that centripetal force is not a new force but the net force resulting from all forces acting on the object in circular motion.
At the top of the circle, the gravitational force and tension force combine to provide the centripetal force, and they act in the same direction.
The minimum speed of the ball at the top of the circle (Point Z) can be derived using the formula mg = m*v^2/r.
When the string breaks, the ball will fly off in the direction of its instantaneous velocity, which is tangent to the circle.
The ball's motion after the string breaks is described as projectile motion, with an upward trajectory followed by a descent.
The velocity of the ball decreases as it ascends to its maximum height and becomes zero at the peak of its trajectory.
The only acceleration acting on the ball after the string breaks is due to gravity, which is directed downwards.
The concept of centripetal force is fundamental in understanding circular motion and is a combination of forces like tension and gravity.
The free body diagram is a crucial tool in visualizing and analyzing the forces acting on an object in circular motion.
The mathematical derivation of the minimum speed involves algebraic manipulation of the forces acting on the ball.
The example problem provided illustrates the application of the concepts discussed in the transcript.
The transcript serves as a comprehensive guide for students learning about circular motion and the forces involved.
Understanding the net force and its components is essential for solving physics problems involving circular motion.
Transcripts
Browse More Related Video

Centripetal force problem solving | Centripetal force and gravitation | Physics | Khan Academy

Uniform Circular Motion Free Body Diagrams

High School Physics - Centripetal Force
Physics - What Is a Centripetal Force?

What is Vector Acceleration in Physics? (Centripetal, Instantaneous & Average Acceleration) -[1-4-2]

Changing Velocity | Forces & Motion | Physics | FuseSchool
5.0 / 5 (0 votes)
Thanks for rating: