High School Physics - Centripetal Force
TLDRIn this informative video, Mr. Fullerton explains the concept of centripetal force, clarifying that it is not a unique type of force but rather a label for the force that causes centripetal acceleration towards the center of a circular path. He demonstrates how to calculate centripetal force using Newton's second law and provides several examples involving a car on a circular track, a ball on a string, and a bucket of water being slung in a circle. The video effectively illustrates the application of physics principles in real-world scenarios.
Takeaways
- 📚 Centripetal force is not a unique or magical force; it's a term used to describe a force that causes centripetal acceleration towards the center of a circular path.
- 🚗 In the context of circular motion, an object experiences a centripetal acceleration, which requires a force directed towards the center of the circle.
- 📐 Newton's second law (F = ma) is fundamental in understanding centripetal force; a force is needed to cause an acceleration.
- 🔄 When an object moves in a circular path at constant speed, it is still accelerating due to the change in direction, which is described as centripetal acceleration.
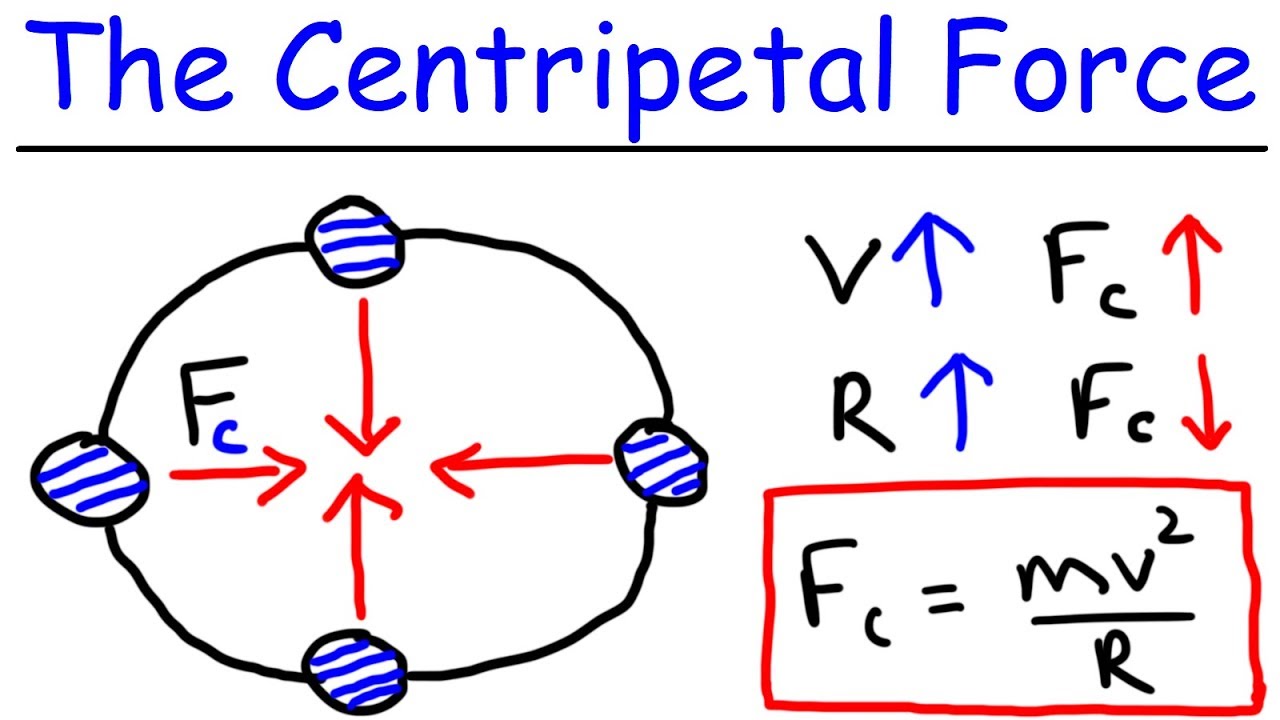
- 🚀 To calculate centripetal force, use the formula Fc = mv^2/r, where Fc is the centripetal force, m is the mass, v is the velocity, and r is the radius of the circular path.
- 🎯 The direction of centripetal force (and thus acceleration) is always towards the center of the circle, which is tangential to the circle at any given point.
- 🚗 In the example of a car on a circular track, the direction of velocity is tangential, and the direction of centripetal force is radial, towards the center.
- 🏆 When an object in circular motion loses the force causing centripetal acceleration (like friction), it will move in a straight line according to Newton's first law.
- 🏀 For the example of a ball on a string, releasing the string at the point where the ball's trajectory is tangent to the circle will result in the ball hitting the target.
- 💡 In solving problems, it's essential to identify the actual force causing the centripetal acceleration, such as tension in a string or gravitational force.
- 🔍 The script provides examples of calculating centripetal force for different scenarios, emphasizing the importance of understanding the underlying principles and applying the correct formula.
Q & A
What is the main objective of the discussion on centripetal force in the transcript?
-The main objective is to define centripetal force and understand that it is not a unique or magical force, but rather a label for the force that causes centripetal acceleration towards the center of a circle.
According to Newton's second law, what is required to create an acceleration?
-According to Newton's second law, a force is required to create an acceleration.
What is the formula for calculating centripetal acceleration?
-The formula for centripetal acceleration is V^2 / R, where V is the velocity of the object and R is the radius of the circular path.
In the example of the 1000 kg car, what is the significance of the direction of centripetal force in a circular motion?
-The direction of the centripetal force is always towards the center of the circle, which is necessary for maintaining the car's circular motion and causing the centripetal acceleration.
What happens to the ball in the second example when the string is released?
-When the string is released, the tension that was causing the centripetal force is removed, causing the ball to follow Newton's first law and continue in a straight line tangent to the circle at the release point.
How is the centripetal force calculated for an object in circular motion?
-The centripetal force is calculated using the formula F_net (centripetal direction) = m * (V^2 / R), where m is the mass of the object, V is its velocity, and R is the radius of the circular path.
What is the mass of the 800 Newton running back mentioned in the transcript?
-The mass of the running back is approximately 81.5 kilograms, calculated by dividing the weight (800 Newtons) by the acceleration due to gravity (9.81 m/s^2).
What is the centripetal acceleration of the 800 Newton running back turning a corner with a radius of one meter at a velocity of eight meters per second?
-The centripetal acceleration is 64 m/s^2, calculated using the formula AC = V^2 / R, where V is 8 m/s and R is 1 meter.
What is the magnitude of the centripetal force acting on the 5 kg bucket of water being slung in a circle with a radius of 0.7 meters at a speed of 2 meters per second?
-The magnitude of the centripetal force is approximately 28.6 Newtons, calculated using the formula F = m * (V^2 / R), where m is 5 kg, V is 2 m/s, and R is 0.7 meters.
What would be the direction of the force acting on the 1750 kg car if it were to continue in a circular motion after hitting the ice at point P?
-If the car were to continue in a circular motion, the force would still be directed towards the center of the circle, which is the definition of centripetal force. However, since the car loses all frictional force on its tires, it will not continue in a circular path but rather travel in a straight line.
What is the centripetal force acting on the 1750 kg car traveling at a constant speed of 15 meters per second around a horizontal circular track with a radius of 45 meters?
-The centripetal force acting on the car is 8,750 Newtons, calculated using the formula F = m * (V^2 / R), where m is 1750 kg, V is 15 m/s, and R is 45 meters.
Outlines
📚 Introduction to Centripetal Force
This paragraph introduces the concept of centripetal force, emphasizing that it is not a unique or magical type of force but rather a label for the net force acting towards the center of a circle that causes centripetal acceleration. The main objective is to define centripetal force and understand its role in circular motion. It also sets the stage for solving problems related to the calculation of centripetal force. The paragraph discusses Newton's second law in the context of circular motion, highlighting that an object moving in a circle is accelerating towards the center, hence experiencing centripetal acceleration. It explains that this acceleration is a result of a force, which is termed as centripetal force (Fc). The content also touches on the fact that the actual force causing centripetal force could be friction or gravity, and these should be represented in a Freebody diagram instead of a generic centripetal force. The paragraph concludes with a series of questions to apply the concept, such as determining the correct point to release a ball moving in a circular path to hit a target and the behavior of a car losing friction while turning.
🔢 Calculation of Centripetal Force in Various Scenarios
This paragraph delves into the calculation of centripetal force in different scenarios, providing a clear understanding of how to determine the magnitude of this force. It begins by explaining the formula for centripetal acceleration (V^2/R) and how it relates to the force (F = m*a_c). The paragraph then applies this knowledge to real-world examples, such as a car moving in a circular track, a ball moving in a circular path, and a bucket of water being slung in a circle. Each example is used to demonstrate the calculation of centripetal force, taking into account factors like mass, velocity, and radius. The paragraph also discusses the role of tension in a string or friction in maintaining the circular motion and how the absence of these forces affects the motion of the objects. The detailed calculations and explanations help to solidify the understanding of centripetal force and its applications in physics.
Mindmap
Keywords
💡Centripetal Force
💡Centripetal Acceleration
💡Newton's Second Law
💡Velocity
Highlights
Centripetal force is defined and recognized as not a special or magical force, but a label for a force causing centripetal acceleration.
The force causing centripetal acceleration is labeled as FC (centripetal force) according to Newton's second law.
In a free body diagram, the force causing centripetal acceleration is identified as the actual force at work, such as friction or gravity, not a separate 'centripetal force'.
An object traveling in a circular path at constant speed experiences a centripetal acceleration towards the center of the circle.
A car traveling on a circular track provides an example of centripetal force in action, with its direction towards the center of the circle.
The concept of releasing a ball moving in a circular path to hit a target is discussed, relating to the tangent line at the release point.
A car hitting ice and losing frictional force demonstrates the transition from circular motion to straight-line motion due to the loss of centripetal force.
Calculating centripetal force involves using the formula F_net = m*a_c, where a_c is the centripetal acceleration calculated by v^2/R.
The example of an 800 Newton running back turning a corner illustrates the calculation of mass, centripetal acceleration, and force.
A 5 kg bucket of water being slung in a circle demonstrates the calculation of centripetal force due to tension in the string.
The example of a 1750 kg car traveling at a constant speed around a circular track shows the calculation of the centripetal force acting on the car.
The importance of understanding the relationship between mass, velocity, and radius in calculating centripetal force is emphasized.
The practical application of centripetal force is shown through examples involving cars and a bucket of water.
The concept of centripetal force and acceleration is rooted in Newton's laws of motion.
The transcript provides a comprehensive overview of centripetal force, including its definition, calculation, and examples.
The discussion on centripetal force bridges theoretical physics with real-world scenarios, enhancing understanding and application.
Transcripts
Browse More Related Video

Centripetal force problem solving | Centripetal force and gravitation | Physics | Khan Academy

Uniform Circular Motion Free Body Diagrams

Understanding Circular Motion

Centripetal force and acceleration intuition | Physics | Khan Academy

What Is Circular Motion? | Physics in Motion
Physics - What Is a Centripetal Force?
5.0 / 5 (0 votes)
Thanks for rating: