Worked example: Implicit differentiation | Advanced derivatives | AP Calculus AB | Khan Academy

Khan Academy
30 Jan 201304:55
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a step-by-step guide on performing implicit differentiation, a crucial technique in calculus. It begins by setting up the problem, assuming y is a function of x, and then applies the derivative operator to an equation involving x and y. The chain rule is used to find the derivative of the left side of the equation, while the right side involves the derivative of x and a constant. The process involves simplifying and rearranging terms to solve for the derivative of y with respect to x, resulting in a final expression that gives the derivative in terms of y and x.

Takeaways
  • 📚 The topic is implicit differentiation, focusing on finding the derivative of y with respect to x when y is a function of x.
  • 🔍 The derivative operator is applied to both sides of the given equation, emphasizing the use of the chain rule for the left-hand side.
  • 📈 The chain rule is applied to the term (x - y^2), resulting in 2x - 2y^1 times the derivative of x - y with respect to x.
  • 🌟 The derivative of x with respect to x is 1, while the derivative of y with respect to x is the unknown we are solving for, denoted as dy/dx.
  • 🤔 The right-hand side of the equation simplifies to 1 (derivative of x) plus the derivative of y with respect to x (dy/dx), and 0 (derivative of a constant).
  • 🧩 The process involves solving for dy/dx by isolating it on one side of the equation through algebraic manipulation.
  • 📊 By rewriting and distributing terms, we aim to get all dy/dx terms on one side and the non-dy/dx terms on the other.
  • 🎯 After simplification, the equation becomes (2y - 2x - 1) times dy/dx equals 1 - 2x + 2y.
  • 📝 To solve for dy/dx, we divide both sides of the equation by (2y - 2x - 1), yielding the final expression for the derivative of y with respect to x.
  • 🌐 The key to solving this problem is understanding the chain rule and carefully performing algebraic operations to isolate dy/dx.
  • 🎓 The final result is the derivative of y with respect to x, expressed as (2y - 2x + 1) / (2y - 2x - 1).
Q & A

  • What is the main topic of the script?

    -The main topic of the script is implicit differentiation, specifically finding the derivative of y with respect to x given an equation.

  • What is the initial assumption made in the script?

    -The initial assumption made in the script is that y is a function of x.

  • What mathematical rule is first applied to the left-hand side of the equation?

    -The chain rule is first applied to the left-hand side of the equation.

  • What does the chain rule give us in this context?

    -In this context, the chain rule gives us the derivative of (x - y^2) with respect to x, which is 1 - (dy/dx).

  • What is the derivative of a constant with respect to x?

    -The derivative of a constant with respect to x is 0.

  • How does the script simplify the expression 2x - 2y?

    -The script simplifies the expression 2x - 2y by distributing the 2 across x and y, resulting in 2x - 2y = 2(x - y).

  • What is the final expression for the derivative of y with respect to x, dy/dx?

    -The final expression for the derivative of y with respect to x, dy/dx, is (2y - 2x + 1) / (2y - 2x - 1).

  • What is the key step in solving for dy/dx?

    -The key step in solving for dy/dx is rearranging the terms to isolate dy/dx on one side of the equation and then dividing both sides by the expression (2y - 2x - 1).

  • How does the script demonstrate the process of implicit differentiation?

    -The script demonstrates the process of implicit differentiation by applying the derivative operator to both sides of an equation, using the chain rule, simplifying the expression, and then solving for the unknown derivative.

  • What is the significance of the final expression for dy/dx obtained in the script?

    -The significance of the final expression for dy/dx is that it represents the derivative of y with respect to x, which is the main objective of the exercise and can be used for further analysis or in other mathematical contexts.

  • What algebraic technique is used to isolate dy/dx?

    -The algebraic technique used to isolate dy/dx is subtracting 2x - 2y and dy/dx from both sides of the equation to separate the terms involving dy/dx from those that do not.

Outlines
00:00
📚 Implicit Differentiation Practice

This paragraph introduces the concept of implicit differentiation, emphasizing the need for more practice to master the technique. The speaker guides the audience through the process of finding the derivative of 'y' with respect to 'x', assuming 'y' is a function of 'x'. The explanation includes applying the derivative operator to both sides of an equation, utilizing the chain rule on the left-hand side, and simplifying the expression to isolate the derivative of 'y' with respect to 'x'. The paragraph concludes with the derived formula for the derivative, expressed as (2y - 2x + 1) / (2y - 2x - 1), highlighting the algebraic process required to solve for 'dy/dx'.

Mindmap
Keywords
💡Implicit Differentiation
Implicit differentiation is a method used in calculus to find the derivative of a function when the function is not explicitly given in terms of y as a function of x. It involves differentiating both sides of an equation with respect to x, using the chain rule and other differentiation techniques. In the video, the process of implicit differentiation is applied to the equation x^2 - y^2 and the steps are outlined to find the derivative dy/dx, which is the main focus of the video's content.
💡Derivative Operator
The derivative operator, often denoted as 'd/dx' or 'dy/dx', represents the process of finding the derivative of a function with respect to a variable. It is a fundamental concept in calculus, used to determine the rate of change or slope of a curve at any given point. In the context of the video, the derivative operator is applied to both sides of the equation to find the derivative of y with respect to x.
💡Chain Rule
The chain rule is a fundamental rule in calculus that is used to find the derivative of a composite function. It states that the derivative of a function composed of other functions is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is applied when differentiating the left-hand side of the equation, where y is a function of x.
💡Rate of Change
The rate of change, or the derivative, represents the speed at which a quantity changes with respect to another quantity. In the context of the video, the rate of change is used to describe how the value of y changes as x changes, which is the goal of the implicit differentiation process.
💡Algebra
Algebra is a branch of mathematics concerned with solving equations and understanding the relationships between quantities. In the video, algebraic manipulation is crucial for simplifying and solving for the unknown derivative, dy/dx. It involves distributing, combining like terms, and isolating the variable of interest.
💡Constant
In mathematics, a constant is a value that does not change. In the context of differentiation, the derivative of a constant is always zero because there is no rate of change associated with a constant value. The video mentions that the derivative of a constant with respect to x is 0, which is a basic rule of calculus.
💡Solving Equations
Solving equations involves finding the values of the variables that make the equation true. In the video, the process of solving for the derivative dy/dx involves rearranging the terms and isolating the desired variable on one side of the equation. This requires a good understanding of algebraic principles.
💡Derivative of x with respect to x
The derivative of a variable with respect to itself is always 1. This is a basic rule in calculus and is used in the process of differentiating functions. In the video, when differentiating the term x with respect to x, the result is 1, which is a straightforward application of this rule.
💡Differential Equation
A differential equation is an equation that involves an unknown function and its derivatives. In the video, the given equation x^2 - y^2 = C is a type of differential equation, where the goal is to find the derivative of y with respect to x, which is not explicitly given in terms of x.
💡Slope
The slope of a curve at a particular point is a measure of how steep the curve is at that point. It is the coefficient of x in the equation of the tangent line to the curve at that point. In the context of the video, the slope is represented by the derivative dy/dx, which describes the rate of change of y with respect to x.
💡Rate of Change Interpretation
The interpretation of the rate of change, or derivative, in a practical sense is understanding how one quantity varies as another quantity varies. In the context of the video, the rate of change interpretation is used to describe the steepness or slope of the curve defined by the equation x^2 - y^2 at any given point.
Highlights

The process of implicit differentiation is introduced, which is a key concept in calculus.

The assumption that y is a function of x is fundamental to the problem-solving approach.

The application of the derivative operator to both sides of the equation is a critical step in the process.

The use of the chain rule is highlighted as essential in differentiating the left-hand side of the equation.

The derivative of x with respect to x is identified as 1, a basic calculus fact.

The goal of solving for the derivative of y with respect to x (dy/dx) is clearly stated.

The algebraic manipulation of terms, including the distribution of 2, is a key part of the process.

The simplification of the equation by combining like terms is demonstrated.

The strategy of isolating dy/dx on one side of the equation is explained.

The subtraction of non-dy/dx terms from both sides to simplify the equation is a highlighted technique.

The final form of the derivative of y with respect to x is derived and presented.

The importance of the algebraic steps in solving for dy/dx is emphasized.

The solution is expressed in a simplified fraction, showcasing the final result of the differentiation process.

The method of solving for dy/dx is applicable to a wide range of mathematical problems.

The transcript serves as a comprehensive guide for those learning implicit differentiation.

The clear and step-by-step explanation ensures the process is accessible to a broad audience.

The practical application of the chain rule in implicit differentiation is demonstrated.

The transcript provides a solid foundation for further exploration of calculus concepts.

Transcripts

Browse More Related Video

Second derivatives (implicit equations): find expression | AP Calculus AB | Khan Academy

How to use implicit differentiation on an equation for dy dx

Implicit Differentiation for Calculus - More Examples #2

Implicit Differentiation for Calculus - More Examples, #1

Implicit Differentiation - More Examples

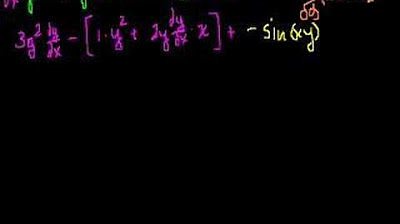
Implicit Differentiation (part 2)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsDifferentiationEducationAlgebraCalculusProblem SolvingTeachingMath TutorialImpulseLearning