Integration by parts: ºx____dx | AP Calculus BC | Khan Academy

Khan Academy
28 Jan 201306:45
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a step-by-step walkthrough of using integration by parts to find the antiderivative of a complex function, x squared times e to the x. The process involves recognizing when integration by parts is applicable, assigning functions f(x) and g'(x), and iteratively applying the integration by parts formula to simplify the expression. The example demonstrates how to reduce the complexity of the integral by taking derivatives and antiderivatives strategically, ultimately arriving at the simplified antiderivative, x squared e to the x minus 2xe to the x plus 2e to the x plus C.

Takeaways
  • 📚 The problem involves finding the antiderivative of the product of x squared and e to the power of x (x^2 * e^x).
  • 🧠 Integration by parts is identified as a suitable method for solving this integral due to the product of two functions, where one can be simplified by differentiation and the other by integration.
  • 🔄 The process starts by assigning f(x) = x^2, which simplifies to f'(x) = 2x, and g'(x) = e^x, with the antiderivative g(x) = e^x.
  • 📈 The integration by parts formula is applied, resulting in x^2 * e^x minus the antiderivative of the product of f'(x) and g(x).
  • 🎯 The next step involves focusing on the simpler integral of x * e^x, which is again approached with integration by parts, assigning f(x) = x and g'(x) = e^x.
  • 🤝 The second application of integration by parts yields the antiderivative as x * e^x minus the antiderivative of e^x, which is e^x.
  • 🔢 Substituting the results back into the original expression, we obtain the antiderivative as x^2 * e^x - 2 * x * e^x + 2 * e^x, plus a constant of integration (C).
  • 🌟 The key to solving complex integrals is breaking them down into simpler parts and reusing the same method, such as integration by parts, as necessary.
  • 📊 The process demonstrates the power of recognizing patterns and applying the same technique iteratively to simplify increasingly complex expressions.
  • 🎓 Integration by parts is a fundamental technique in calculus that allows for the simplification of products of functions into more manageable forms.
  • 🔍 The solution requires careful tracking of the constants and the derivatives and antiderivatives of the functions involved in the integral.
Q & A

  • What is the integral of x squared times e to the x dx?

    -The integral of x squared times e to the x dx can be found using integration by parts, a method that simplifies the product of two functions by converting it into a sum involving the derivatives and antiderivatives of those functions.

  • Why is integration by parts applicable in this case?

    -Integration by parts is applicable when dealing with the product of two functions, where one function can be simplified by taking its derivative and the other can be made less complicated by taking its antiderivative.

  • What are the functions f(x) and g'(x) assigned to be in the first attempt of integration by parts?

    -In the first attempt, f(x) is assigned to be x squared, and g'(x) is assigned to be e to the x.

  • What does the integration by parts formula look like?

    -The integration by parts formula is ∫u dv = uv - ∫v du, where u and v are functions of x, and their derivatives and antiderivatives are represented by u' and v' respectively.

  • What is the antiderivative of e to the x?

    -The antiderivative of e to the x is simply e to the x, as the exponential function is its own integral.

  • How is the degree of x squared reduced in the process?

    -The degree of x squared is reduced by applying integration by parts, which results in a simpler expression involving 2x, thus lowering the degree of the polynomial.

  • What is the purpose of taking constants out of the integral sign?

    -Taking constants out of the integral sign simplifies the integral by allowing the constant to be factored out, which is only possible for constants multiplying the function being integrated.

  • What is the second application of integration by parts for?

    -The second application of integration by parts is for the integral of x times e to the x dx, which arises after the first application of integration by parts.

  • What functions are f(x) and g'(x) redefined as in the second attempt?

    -In the second attempt, f(x) is redefined as x, and g'(x) remains e to the x.

  • What is the final result of the antiderivative of x squared times e to the x dx?

    -The final result of the antiderivative is x squared e to the x minus 2xe to the x plus 2e to the x, plus a constant of integration, denoted as C.

  • How does the process of integration by parts simplify complex integrals?

    -Integration by parts simplifies complex integrals by breaking down the product of functions into a series of simpler integrals and known antiderivative forms, allowing for easier computation and understanding.

Outlines
00:00
📚 Introduction to Integration by Parts

The paragraph begins by introducing the concept of taking the antiderivative of a function, specifically focusing on the product of two functions: x squared times e to the power of x. The speaker, Sal, explains the applicability of integration by parts in this scenario, emphasizing the importance of simplifying one function through differentiation and the other through integration. He assigns f(x) as x squared, noting that its derivative becomes simpler (2x), and g'(x) as e to the x, acknowledging that its antiderivative remains e to the x. Sal then applies the integration by parts formula, leading to a new integral expression involving x times e to the x, which he plans to solve using the same integration by parts technique.

05:01
🔄 Solving the Integral Using Integration by Parts Again

In this paragraph, Sal continues to work on the antiderivative of the original expression by applying integration by parts for the second time. He simplifies the new integral expression by identifying x as the function to differentiate for simplicity, setting f(x) as x and g'(x) as e to the x. After applying the integration by parts formula, Sal finds the antiderivative of the expression involving 1 times e to the x, which simplifies to e to the x. He then substitutes this result back into the previous expression to find the antiderivative of the original function. The final result, after including the constant of integration (C), is a clear and simplified expression: x squared e to the x minus 2xe to the x plus 2e to the x.

Mindmap
Keywords
💡antiderivative
The antiderivative is a fundamental concept in calculus, referring to the reverse process of differentiation. It is used to find the original function from its derivative. In the context of the video, the antiderivative of a function is sought to solve integral calculus problems, specifically for the given expression x squared times e to the x dx. The process involves isolating and integrating parts of the expression to simplify and solve for the antiderivative.
💡integration by parts
Integration by parts is a technique in integral calculus used to evaluate integrals by breaking down the product of two functions into simpler components. The method is based on the product rule for derivatives and is particularly useful when one of the functions in the product can be easily differentiated and the other can be easily integrated. In the video, integration by parts is applied twice to solve the complex integral of x squared times e to the x. The process involves choosing functions u and dv, differentiating u, and integrating dv, to find the integral.
💡e to the x
Euler's number, commonly denoted as 'e', is a fundamental mathematical constant approximately equal to 2.71828. 'e to the x' represents the exponential function, which is a key concept in calculus and many other areas of mathematics. In the video, 'e to the x' is a part of the integrand, and its antiderivative remains 'e to the x', which is a property of exponential functions that makes them unique and useful in integration.
💡derivative
A derivative is a concept in calculus that represents the rate of change of a function with respect to its independent variable. It gives us the slope of the tangent line at any point on the curve of the function, which can be used to analyze various properties of the function, such as its critical points, local maxima and minima, and rate of change. In the context of the video, the derivative of x squared is 2x, which is used in the integration by parts process to simplify the given integral expression.
💡constant
A constant is a value that does not change; it remains the same in all situations. In mathematics and particularly in calculus, constants play a significant role in equations and formulas. The video script mentions constants in the context of integration, where they can be factored out of the integral sign, simplifying the process of finding antiderivatives.
💡product rule
The product rule is a fundamental rule in calculus that describes how to differentiate the product of two or more functions. According to the product rule, the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function. Although not explicitly mentioned in the video, the product rule is implicitly used in the process of integration by parts, which is derived from the product rule for derivatives.
💡simplify
To simplify in mathematics means to make a complex expression or equation more straightforward or easier to understand or work with. This often involves reducing the number of terms, lowering the degree of polynomials, or breaking down complex structures into more basic components. In the video, the process of simplification is crucial as the integrand, x squared times e to the x, is broken down and simplified through the application of integration by parts and other algebraic manipulations.
💡integral
An integral is a mathematical concept that represents the accumulation of a quantity, often understood as the area under a curve. In calculus, integrals are used to find the original function (antiderivative) from its derivative or to calculate the accumulated change over an interval. The video is focused on solving a specific integral, which is the antiderivative of x squared times e to the x dx, using the method of integration by parts.
💡function
A function is a mathematical relationship that assigns a unique output value to each input value. Functions are essential in calculus as they represent relationships between variables, and operations such as differentiation and integration are performed on functions. In the context of the video, functions x squared and e to the x are the core components of the integral being solved. The process of integration by parts involves taking derivatives and antiderivatives of these functions to find the antiderivative of their product.
💡variable
A variable is a symbol, often a letter from the alphabet, that represents a quantity that can change or vary. In mathematics and calculus, variables are used to denote unknowns or values that can be different in different instances. In the video, 'x' is the variable that appears in both the function x squared and the exponential function e to the x, and the process of finding the antiderivative involves working with this variable in different contexts and operations.
Highlights

The problem discussed is finding the antiderivative of x squared times e to the x dx.

Integration by parts is suggested as a method to tackle the problem due to the product of two functions.

The function x squared is chosen as f(x) because its derivative becomes simpler.

The function e to the x is chosen as g'(x) because its antiderivative remains the same, simplifying the process.

The integration by parts formula is applied with f(x) as x squared and g'(x) as e to the x.

The antiderivative of x squared is 2x, simplifying the expression.

The process results in another integral of xe to the x dx, which requires further integration by parts.

For the second integration by parts, x is chosen as f(x) and e to the x as g'(x).

The antiderivative of the product of 1 and e to the x is found to be e to the x.

The final antiderivative expression is simplified to x squared e to the x minus 2xe to the x plus 2e to the x plus C.

The problem-solving process demonstrates the power and utility of integration by parts in calculus.

The video content is educational, providing a step-by-step guide to solving complex integrals.

The method helps to reduce the complexity of the original expression by breaking it down into simpler components.

The explanation is clear and methodical, making it accessible for learners at various levels of mathematical understanding.

The use of color-coding in the explanation aids in distinguishing between different stages of the calculation.

The solution showcases the importance of recognizing when to apply integration by parts based on the properties of the functions involved.

The process emphasizes the need to manage constants effectively when applying integration techniques.

The video serves as a practical example of how to tackle seemingly complex mathematical problems with the right approach.

The final result is a comprehensive solution that combines the insights gained from each step of the integration by parts process.

Transcripts

Browse More Related Video

Integration by parts: ºln(x)dx | AP Calculus BC | Khan Academy

Indefinite Integral

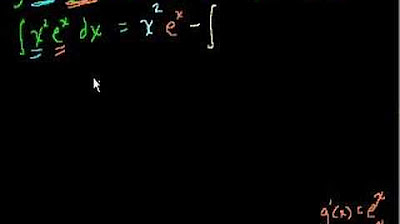
Integration by Parts (part 6 of Indefinite Integration)

Calculus - Integration By Parts

Definite integral involving natural log | AP Calculus AB | Khan Academy

Integration by parts: º___cos(x)dx | AP Calculus BC | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusIntegrationBy PartsMath TutorialDifferential EquationsEducational ContentMathematicsAdvanced MathOnline LearningAcademic