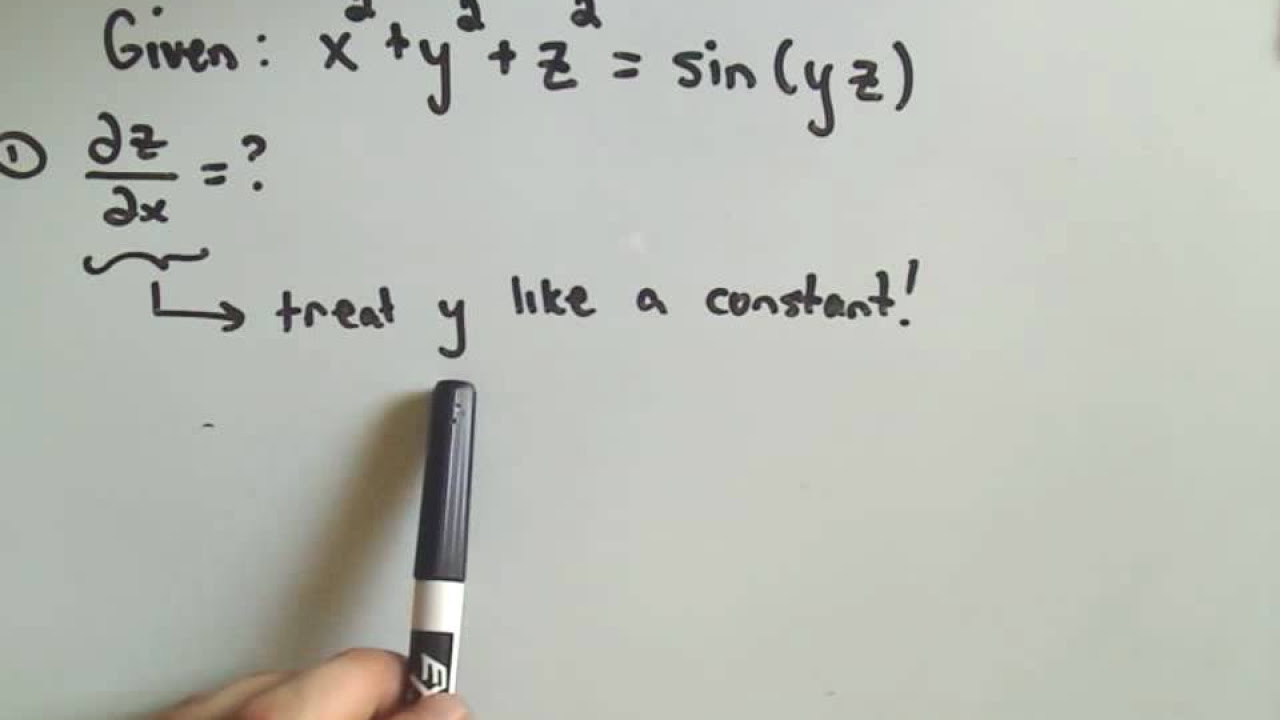Partial derivatives | Multivariable Calculus | Khan Academy

Khan Academy
9 Aug 200811:11
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the concept of functions in three dimensions, focusing on surfaces defined by z as a function of x and y. It explains the right-handed coordinate system and introduces the concept of partial derivatives, illustrating how to calculate the slope of a surface with respect to a particular direction. The video uses an example of a surface defined by the equation z = x^2 + xy + y^2, and demonstrates how to find the partial derivative with respect to x, providing a clear understanding of the rate of change along the x-axis while holding y constant.

Takeaways
  • 📈 Expanding calculus knowledge to three dimensions involves understanding functions in 3D, such as lines, curves, surfaces, and vector fields.
  • 📊 Visualization of 3D functions is not always intuitive and often requires the use of computer graphics.
  • 🌐 In a 3D coordinate system, the x, y, and z axes follow the right-hand rule, with the cross product of x and y yielding z.
  • 📱 A surface in three dimensions can be defined by a function z = f(x, y), where an x and y value corresponds to a z value.
  • 📍 Plotting points on a 3D surface involves incrementing along the x and y axes and then moving up along the z axis based on the function's value.
  • 🤔 Calculus on surfaces requires understanding the concept of slope in 3D, which depends on the direction of the tangent line.
  • 🧭 The slope of a surface at any given point is not unique and depends on the direction in which the slope is being measured.
  • 🔄 At any point on a surface, there are an infinite number of tangent lines, each with a different slope based on its orientation.
  • 📝 Partial derivatives are used to calculate the slope of a surface in a specific direction while holding other variables constant.
  • 🌟 The equation of the example surface given is z = x^2 + xy + y^2, and its partial derivatives can be calculated to find slopes in different directions.
Q & A

  • What does the transcript discuss in relation to three dimensions?

    -The transcript discusses the concept of functions in three dimensions, including lines, curves, surfaces, and vector fields, with a focus on surfaces and their representation using calculus.

  • How does the speaker describe the three-dimensional coordinate system?

    -The speaker describes the three-dimensional coordinate system by adding a third axis for height, called the z-axis, and explains the right-hand rule for the orientation of the axes.

  • What is the significance of the right-hand rule in the context of the coordinate system?

    -The right-hand rule is significant because it establishes the convention for the orientation of the coordinate system, where the cross product of the x-axis with the y-axis equals the z-axis, helping to define the direction of each axis.

  • How can a surface in three dimensions be defined?

    -A surface in three dimensions can be defined by a function where z is a function of x and y, meaning that for every pair of x and y values, there is a corresponding z value.

  • What is the process for plotting points on a surface?

    -To plot points on a surface, one must follow the function definition by substituting specific x and y values into the function to find the corresponding z value, and then plot these points in three-dimensional space.

  • Why is it necessary to specify a direction when taking a derivative in three dimensions?

    -Specifying a direction is necessary because a point on a surface has an infinite number of tangent lines, each with a different slope. The direction of the derivative determines the specific tangent line and its slope at that point.

  • What is a partial derivative and how is it used?

    -A partial derivative is a derivative that considers the change in a function with respect to one variable while keeping all other variables constant. It is used to find the slope or rate of change of a surface along a specific direction in three-dimensional space.

  • How is the equation of the surface z = x^2 + xy + y^2 related to the partial derivative with respect to x?

    -The equation of the surface z = x^2 + xy + y^2 allows us to calculate the partial derivative with respect to x, which is ∂z/∂x = 2x + y. This represents the slope of the surface in the x-direction at any given point (x, y).

  • What does the slope of 0.7 for the function at the point (0.2, 0.3) signify?

    -The slope of 0.7 signifies that for every increase of 1 in the x-value at the point (0.2, 0.3), the z-value increases by 0.7 units. This gives us the rate of change or slope of the surface along the x-direction at that specific point.

  • How does the speaker visualize the concept of the slope of a surface?

    -The speaker visualizes the slope of a surface by considering the rate of change of z with respect to x, represented by the partial derivative. This is demonstrated by the increase in height (z) as x increases, with the slope being less than a 45-degree angle.

  • What is the importance of understanding partial derivatives in the context of three-dimensional calculus?

    -Understanding partial derivatives is crucial in three-dimensional calculus as it allows us to analyze the behavior of functions and surfaces in three-dimensional space, including their slopes, curvature, and rates of change along specific directions.

Outlines
00:00
📈 Introduction to 3D Functions and Coordinate Systems

This paragraph introduces the concept of functions in three dimensions, highlighting the different types of representations such as lines, curves, surfaces, and vector fields. It emphasizes the challenge of visualizing these in three dimensions, especially when moving towards higher dimensions. The discussion then focuses on the most intuitive representation, which is a surface in three dimensions. The paragraph sets the stage for exploring 3D calculus by introducing the third dimension of height and explaining the right-hand rule for the coordinate system. It explains how to define a surface using the function z as a function of x and y, and provides an example of plotting points on a surface. The paragraph also touches on the use of computer-generated graphics for visualizing these surfaces.

05:01
📊 Visualizing and Defining 3D Surfaces

This paragraph delves deeper into the visualization and definition of 3D surfaces. It explains how to represent the x, y, and z axes in a three-dimensional space and how to plot points on a surface using the function z as a function of x and y. The paragraph uses an example to illustrate how to calculate the z-value for given x and y coordinates. It also introduces the concept of computer-generated surfaces and provides a brief demonstration of how to plot and visualize these surfaces. The discussion then transitions to the application of calculus to surfaces, emphasizing the need to specify a direction when taking a derivative in three dimensions.

10:04
🔢 Calculating Partial Derivatives and Understanding Tangent Slopes

This paragraph focuses on the concept of partial derivatives and their application in understanding the slope of a surface at a given point. It explains the process of taking the partial derivative of a function with respect to one variable while holding the other variables constant. The paragraph provides a clear example of calculating the partial derivative of z with respect to x, using a specific function of x and y. It then interprets the meaning of this partial derivative in terms of the slope of the surface, demonstrating how it can be used to determine the rate of change of the height (z) with respect to x at a particular point. The explanation includes a practical visualization of the slope and concludes with an example calculation of the slope at a specific point on the surface.

Mindmap
Keywords
💡Three Dimensions
Three dimensions refer to the concept of a spatial space that is described by three coordinates: x, y, and z. In the context of the video, it is used to explain how functions and surfaces can be represented and visualized in a 3D space, expanding upon the traditional two-dimensional understanding of calculus. The introduction of the third dimension adds complexity and depth to the visualization and analysis of functions, allowing for a more comprehensive exploration of mathematical concepts.
💡Surface
A surface in the context of the video refers to a three-dimensional shape that is defined by a function of two variables, typically x and y. Surfaces are a way to represent complex relationships between variables and can be visualized in 3D space. They are used to understand the behavior of functions in three dimensions, including their slopes and curvatures at different points.
💡Vector Field
A vector field is a collection of vectors that are defined at each point in a particular region of space. In the context of the video, vector fields are one of the representations used to describe functions in three dimensions. They provide a visual way to understand the direction and magnitude of quantities at various points in space, which can be useful in areas such as physics and engineering for modeling phenomena like fluid flow or electromagnetic fields.
💡Cross Product
The cross product is a mathematical operation that takes two vectors in three-dimensional space and produces a third vector that is perpendicular to the first two. In the video, the cross product is used to describe the orientation of the three-dimensional coordinate system, specifically how the z-axis is determined by the cross product of the x-axis and y-axis vectors.
💡Partial Derivative
A partial derivative is a derivative of a function with multiple variables that calculates the rate of change of the function with respect to one variable while keeping the other variables constant. In the video, partial derivatives are used to find the slope of a surface at a particular point, which gives an understanding of how the surface changes in response to changes in one of its variables.
💡Slope
Slope is a measure of the steepness of a line or curve, indicating the rate of change of one quantity with respect to another. In the context of the video, the slope is used to describe the tangent to a surface at a specific point, which provides insight into the direction and rate of change of the surface in three-dimensional space.
💡Right-Handed Coordinate System
A right-handed coordinate system is a convention for a three-dimensional coordinate system where the positive directions of the x, y, and z axes are arranged such that the thumb, index finger, and middle finger of the right hand point in the directions of the i, j, and k unit vectors, respectively, when the hand is positioned to make a right-angle. This convention is used to establish the orientation of the coordinate system and to define the cross product, which is essential for understanding the relationship between the axes and the direction of the resulting vector.
💡Java Applet Grapher
A Java Applet Grapher is a software tool that uses Java applets to create visual representations of mathematical functions and surfaces. In the video, it is mentioned as a resource for generating professional-looking computer graphics of three-dimensional surfaces, which can help visualize complex mathematical concepts more effectively than hand-drawn illustrations.
💡Tangent Line
A tangent line is a line that touches a curve or surface at a single point without crossing it. In the context of the video, the tangent line is used to understand the slope and direction of a surface at a specific point. It represents the instantaneous rate of change and direction of the surface at that point, which is a fundamental concept in calculus when studying the behavior of functions and surfaces.
💡Implicit Derivative
An implicit derivative is a derivative taken with respect to one variable in a function where other variables are considered constant. It is called implicit because the differentiation is done without explicitly expressing the function as a function of the variable with respect to which the derivative is being taken. In the video, the implicit derivative is used to find the partial derivatives of a function of two variables, such as a surface in three dimensions.
Highlights

Expansion of knowledge into three dimensions in calculus.

Different types of representations in three dimensions, such as lines, curves, surfaces, and vector fields.

The challenge of visualizing three-dimensional functions.

The most intuitive representation is a three-dimensional surface.

Introduction to the concept of a three-dimensional coordinate system with x, y, and z axes.

Explanation of the right-hand rule for the three-dimensional coordinate system.

Definition of a surface in three dimensions as z as a function of x and y.

Illustration of how to plot points on a three-dimensional surface.

Use of computer-generated graphics for visualizing three-dimensional surfaces.

The concept of slope on a three-dimensional surface and the need to specify direction.

Introduction to the concept of partial derivatives in three dimensions.

Method for calculating the partial derivative with respect to x while holding y constant.

The equation of the example surface: z = x^2 + xy + y^2.

Explanation of how to find the slope of the surface with respect to x at a given point (x, y).

Visual representation of the slope as the rate of change of z with respect to x.

The practical application of understanding the rate of change in three dimensions for various fields.

Transcripts

Browse More Related Video

Partial derivatives and graphs

Partial Derivatives

Partial derivatives, introduction

What Partial Derivatives Are (Hands-on Introduction) — Topic 67 of Machine Learning Foundations

Functions of Several Variables!

MultiVariable Calculus - Implicit Differentiation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus3D FunctionsSurfacesPartial DerivativesMathematicsVisualizationEducationalHigher MathVector FieldsCross Product