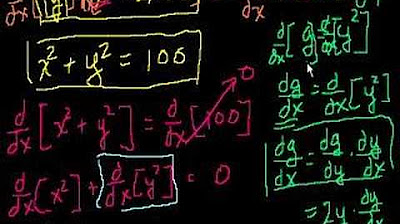Implicit Differentiation
TLDRThe video script introduces the concept of implicit differentiation, a mathematical technique for differentiating functions and relations that are not explicitly defined in terms of the variable with respect to which differentiation is sought. The presenter explains that while this method is part of a higher-level curriculum, it is not overly complex, essentially being an application of the chain rule. Implicit differentiation proves particularly useful for related rates problems. The script provides a step-by-step example using the equation of a circle to illustrate the process of implicit differentiation, contrasting it with the more straightforward explicit differentiation. The presenter emphasizes the utility of implicit differentiation in scenarios where rearranging the equation to make y the subject is not straightforward, highlighting its importance in solving complex calculus problems.
Takeaways
- 📚 Implicit differentiation is a method for differentiating functions and relations, particularly useful when dealing with relations not explicitly defined in terms of the variable you want to differentiate with respect to.
- 🔑 It's essentially an application of the chain rule, given a fancy name, and is part of the syllabus that some students may need to learn, even if it's not for everyone.
- 🎓 The process involves differentiating each term of an equation separately with respect to the variable of interest, without needing to express one variable explicitly in terms of the other.
- 🔍 Useful for related rates questions, where it's not straightforward to rearrange an equation to isolate a variable, implicit differentiation allows for direct differentiation.
- 🌐 When a function isn't defined explicitly in terms of a single variable, implicit differentiation allows you to find the derivative of that function with respect to the variable.
- 📈 The method starts by differentiating both sides of an equation with respect to the variable of interest, treating variables that aren't explicitly defined as functions.
- ⛓ The chain rule is central to implicit differentiation, where you differentiate the 'inside' and then the 'outside' of an expression, similar to how you would with a composite function.
- 🧮 In the context of a circle with a given radius and center at the origin, implicit differentiation helps find the gradient (derivative) at a specific point on the circle without needing to solve for y in terms of x first.
- 📌 At a specific point, you substitute the x and y coordinates into the derivative to find the gradient at that point.
- 🤔 Implicit differentiation can sometimes be more convenient than explicitly rearranging and differentiating, especially in complex related rates problems.
- ➗ The final result of an implicit differentiation is often a ratio involving the derivative of y with respect to x, which can be simplified or evaluated at specific points as needed.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is implicit differentiation, a method for differentiating functions and relations that are not explicitly defined in terms of the variable with respect to which differentiation is sought.
Why is implicit differentiation considered useful?
-Implicit differentiation is considered useful because it is applicable to a whole new family of functions and relations, especially when dealing with related rates questions where explicit differentiation might not be straightforward.
What is the chain rule in the context of implicit differentiation?
-In the context of implicit differentiation, the chain rule is applied when differentiating terms involving 'y' as if 'y' were a function of 'x'. This is done by differentiating the inside function (y) and then the outside function (in this case, squaring y).
How does the process of implicit differentiation differ from explicit differentiation?
-Implicit differentiation does not require the function to be explicitly defined in terms of the variable with respect to which differentiation is performed. It allows differentiation directly from the given relation, treating variables like 'y' as functions.
What is the significance of treating 'y' as a function in implicit differentiation?
-Treating 'y' as a function allows the application of the chain rule to terms involving 'y', even when the explicit form of 'y' in terms of 'x' is not known. This is crucial for implicit differentiation, as it enables the differentiation process to proceed without needing to solve for 'y' first.
Why might implicit differentiation be preferred over explicit differentiation in certain scenarios?
-Implicit differentiation might be preferred when the relation is not easily rearranged to make 'y' the subject, or when dealing with complex relations where explicit differentiation would be cumbersome or impossible. It is particularly handy for related rates problems.
What is the role of the chain rule in differentiating y^2 with respect to x in the given example?
-The chain rule is used to differentiate y^2 with respect to x by first differentiating the inside function (y) and then applying the chain rule to the outside function (the squaring of y), which involves bringing the power down and reducing the power by one.
How does the process of implicit differentiation help in finding the gradient of a circle at a given point?
-Implicit differentiation allows us to find the gradient (rate of change) of a circle at a given point without needing to express y explicitly in terms of x. By differentiating the circle's equation with respect to x and then solving for dy/dx, we can find the gradient at any point on the circle.
What is the final expression for the gradient of the circle at the point (3,4) using implicit differentiation?
-The final expression for the gradient at the point (3,4) is -x/√(25 - x^2). When x equals 3, the gradient is -3/√16, which simplifies to -3/4.
What is the key takeaway from the example of differentiating the circle's equation using both explicit and implicit methods?
-The key takeaway is that while both methods can be used to find the gradient, implicit differentiation offers a more direct approach when explicit rearrangement of the equation is not straightforward or is complex. It is particularly useful for related rates problems and for equations that do not lend themselves easily to explicit differentiation.
How does the transcript demonstrate the application of implicit differentiation to a real-world problem?
-The transcript demonstrates the application of implicit differentiation by using the example of a circle to find the gradient at a specific point. It shows that implicit differentiation is a powerful tool for solving problems where the relationship between variables is given implicitly rather than explicitly.
What is the importance of understanding the distinction between explicit and implicit differentiation?
-Understanding the distinction is important because it allows one to choose the appropriate method for differentiation based on the problem at hand. Knowing when to use implicit differentiation can simplify calculations and make solving complex problems more feasible.
Outlines
📚 Introduction to Implicit Differentiation
The first paragraph introduces the concept of implicit differentiation, which is a method used to differentiate functions and relations. The speaker clarifies that it is a part of the syllabus that not all students are required to learn, but it is taught because it's not too difficult and is very useful, especially for related rates questions. The paragraph explains that implicit differentiation is used when functions are not explicitly defined in terms of the variable we want to differentiate with respect to. An example of a circle's equation is used to illustrate the process of implicit differentiation, contrasting it with the more straightforward explicit differentiation.
🔢 Applying Implicit Differentiation to a Circle's Equation
The second paragraph delves into the process of using implicit differentiation on the equation of a circle with its center at the origin and a radius of five. The speaker demonstrates how to differentiate the circle's equation with respect to x without first solving for y explicitly. The explanation involves applying the chain rule to the y term, treating y as a function of x, and differentiating both the inside and outside of the y squared term. The result is a derivative expression that includes y, which is then simplified and evaluated at a specific point (x=3, y=4) to find the gradient of the circle at that point.
⤵️ Simplifying the Derivative with Implicit Differentiation
The third paragraph continues the discussion on implicit differentiation by simplifying the derivative obtained from the previous paragraph. The speaker shows how to isolate dy/dx to find the gradient of the circle at the point (3,4). The process involves rearranging the terms to solve for dy/dx, which results in a simplified expression of -x/y. The paragraph emphasizes that while the expression still contains y, it is valid because at the specific point (3,4), the values of x and y are known, making it possible to calculate the gradient directly.
Mindmap
Keywords
💡Implicit Differentiation
💡Chain Rule
💡Related Rates
💡Differentiation
💡Circle Relation
💡Gradient
💡Differentiation with Respect to
💡Explicit Function
💡Derivative
💡Fourier Syllabus
💡Product and Quotient Rule
Highlights
Implicit differentiation is a method for differentiating functions and relations, defined in the Fourier syllabus.
It is a four unit method that 40 people have to learn and 300 people don't, but it's still taught due to its usefulness.
Implicit differentiation is essentially just the chain rule with a fancy name.
It is extraordinarily useful for related rates questions.
Implicit differentiation is used when functions aren't defined explicitly in terms of the variable we want to differentiate with respect to.
The method allows you to differentiate without rearranging the equation to make y the subject first.
Treating y as a function and applying the chain rule is the key step in implicit differentiation.
Differentiating y^2 involves differentiating the inside function (y) and then the outside function (squaring).
Implicit differentiation can be applied directly to an equation like x^2 + y^2 = 25 without rearranging.
Differentiating each term separately with respect to x is the approach taken.
The derivative of y^2 is found by differentiating y (the inside function) and then applying the chain rule to the squaring (the outside function).
The resulting derivative dy/dx is expressed in terms of y, which can be evaluated at specific points.
At the point (3,4), the gradient of the circle is found to be -3/4 using implicit differentiation.
Implicit differentiation is particularly handy for related rates questions where rearranging is not straightforward.
The method allows you to find the derivative of relations like a circle without explicitly solving for y first.
It is a powerful technique for differentiating a whole new family of functions that are not explicitly defined in terms of the variable of interest.
Understanding and mastering the chain rule is key to successfully applying implicit differentiation.
The method demonstrates the versatility of the chain rule in a new context beyond just simple variable substitution.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: