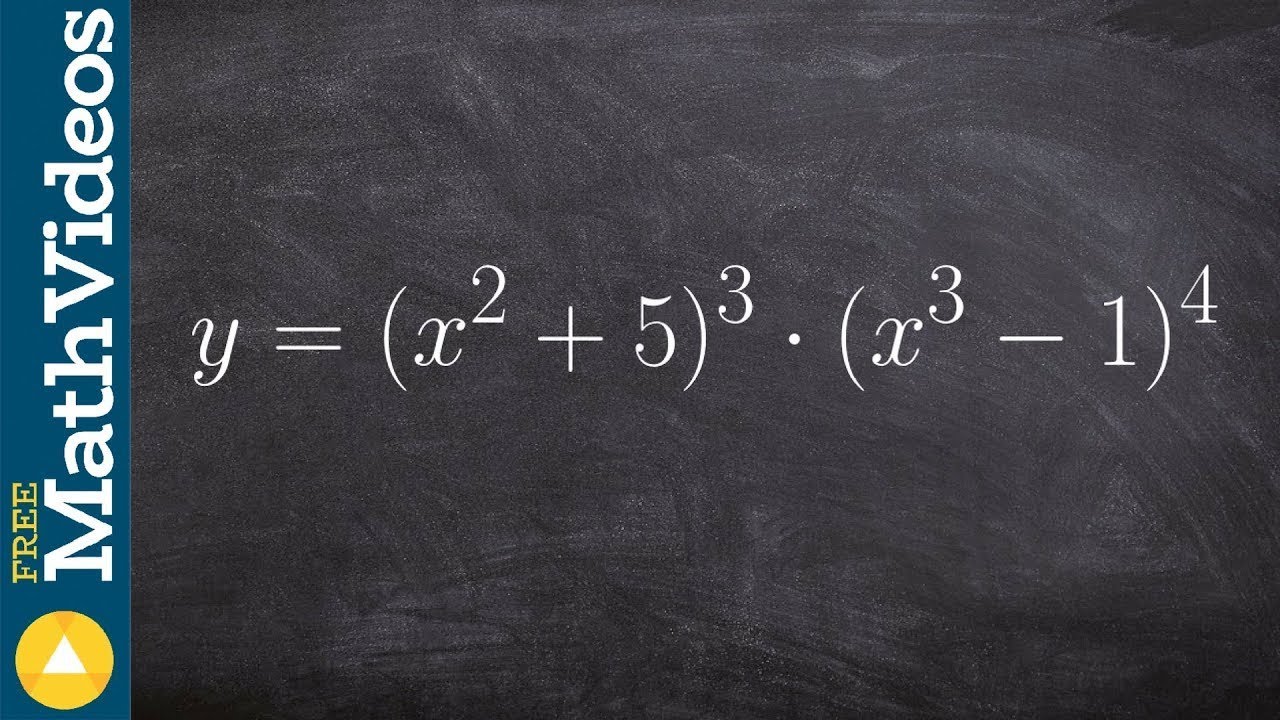Chain Rule Examples

Khan Academy
3 Oct 200709:24
EducationalLearning
32 Likes 10 Comments

TLDRThe video script demonstrates the application of the chain rule in calculus to find the derivative of complex functions. It illustrates the process step by step with two examples, showing how to break down complicated expressions into simpler parts and apply basic derivative rules. The first example involves a polynomial function raised to a negative power, while the second example adds an additional layer of complexity with a function that includes an exponent raised to a power. The script emphasizes the importance of understanding the chain rule to solve more intricate calculus problems and encourages practice to master the concept.

Takeaways
  • 📚 The chain rule is a powerful tool for differentiating complex functions.
  • 🔢 The process involves differentiating the innermost function first and then working outwards.
  • 🌟 Negative exponents follow the same pattern as positive exponents when differentiating.
  • 📈 The derivative of a function can be found by applying the chain rule to each component of the function.
  • 🔄 When applying the chain rule, each step involves taking the derivative of a part of the expression and then multiplying it by the derivative of the remaining part.
  • 📊 The chain rule allows for the calculation of the slope of a function at any point by substituting the point into the derivative equation.
  • 🧠 Understanding the chain rule involves recognizing that the derivative of a composite function is the derivative of the inner function times the derivative of the outer function.
  • 📝 Practice is key to mastering the chain rule, as demonstrated by the presenter's assurance that more examples will help clarify the concept.
  • 🌐 The chain rule can be applied to functions with multiple layers of complexity, such as expressions raised to powers.
  • 🚀 The chain rule is not limited to simple polynomial functions; it can be used for more intricate mathematical expressions.
Q & A

  • What is the chain rule used for in calculus?

    -The chain rule is used in calculus to find the derivative of a composite function, which is a function made up of one function nested inside another function.

  • What is the first example function given in the script?

    -The first example function given in the script is f(x) = x^3 + 2x^2 - x^(-2).

  • How does the script demonstrate the simplification of the derivative of the first example function?

    -The script demonstrates the simplification by first finding the derivative of the innermost part of the function, then multiplying it by the derivatives of the subsequent parts, and finally combining all the terms to get the derivative of the entire function.

  • What is the second example function presented in the script?

    -The second example function presented in the script is f(x) = (3x^(-2) + 5x^3 - 7x)^5.

  • How does the chain rule help in simplifying the derivative of complex functions?

    -The chain rule helps in simplifying the derivative of complex functions by breaking down the function into smaller, more manageable parts. The derivative of each part is calculated and then combined to find the derivative of the entire function.

  • What is the main takeaway from the script regarding the chain rule?

    -The main takeaway is that the chain rule allows us to find the derivative of complicated functions by focusing on the derivatives of their individual parts, which can make the process more manageable and less intimidating.

  • How does the script emphasize the learning process of the chain rule?

    -The script emphasizes that understanding the chain rule is a matter of practice and exposure to various examples. It encourages learners to see multiple examples to gain a better grasp of the concept.

  • What is the result of the derivative of the first example function?

    -The derivative of the first example function is f'(x) = 3x^2 + 4x - 2x^(-3) multiplied by (-7) and then the entire original function to the power of (-8).

  • What is the general process described in the script for finding the derivative of a function using the chain rule?

    -The general process is to start with the innermost function, find its derivative, then multiply it by the derivative of the next outer function, and continue this process until the derivative of the entire composite function is found.

  • What is the significance of the chain rule in advanced calculus?

    -The chain rule is significant in advanced calculus as it is a fundamental tool for differentiating complex functions, which is essential for solving more advanced mathematical problems and applications in various fields.

  • How does the script handle the concept of negative exponents in derivatives?

    -The script explains that when dealing with negative exponents in derivatives, you multiply by the reciprocal of the base (changing the sign) and decrease the exponent by one.

  • What is the final expression for the derivative of the second example function?

    -The final expression for the derivative of the second example function is (15x^2 - 7) * (5x^3 - 7x)^4 * (3x^(-2) - 2)^3.

Outlines
00:00
📚 Applying the Chain Rule to Complex Derivatives

This paragraph introduces the concept of applying the chain rule to calculate the derivative of a complex function. The speaker begins by expressing dissatisfaction with the current tool and moves on to define a new function, f(x) = x^3 + 2x^2 - x^(-2), and then proceeds to explain the process of finding its derivative. The explanation includes taking the derivative of the inner function and then multiplying it by the derivatives of the outer functions. The speaker emphasizes the simplicity of the process despite the complexity of the function and concludes by mentioning the potential to find the slope of the function at any given point.

05:03
🔢 Demonstrating the Chain Rule with Deeper Nesting

In this paragraph, the speaker further illustrates the application of the chain rule by tackling a more complex function, f(x) = (3x^(-2) + 5x^3 - 7x)^3. The speaker outlines the step-by-step process of finding the derivative, starting with the innermost function and working outwards. The explanation includes taking derivatives, multiplying them by the respective outer functions, and adjusting the exponents accordingly. The speaker reassures the audience that despite the complexity, the chain rule can simplify the process significantly. The paragraph concludes with an apology for any confusion and a promise to continue with more chain rule examples in future presentations.

Mindmap
Keywords
💡Chain Rule
The Chain Rule is a fundamental concept in calculus that allows the differentiation of composite functions. In the context of the video, it is used to find the derivative of complex functions by breaking them down into simpler, inner functions and applying the derivative to each part. The Chain Rule is essential for solving more complicated problems where functions are nested or composed of multiple parts. The video demonstrates its application by using the Chain Rule to find the derivative of a polynomial raised to a negative power, illustrating how it simplifies the process and makes it manageable.
💡Derivative
In calculus, the derivative represents the rate of change or the slope of a function at a particular point. It is a crucial concept for understanding how a function behaves as its input changes. The video focuses on teaching how to calculate derivatives using the Chain Rule, emphasizing its importance in analyzing the slope of functions at any given point. Derivatives are used to answer questions about the rate of change, optimization problems, and the behavior of functions, making them a central topic in the study of calculus.
💡Polynomial
A polynomial is a mathematical expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. Polynomials are fundamental in algebra and calculus, and understanding their properties is essential for solving various mathematical problems. In the video, the focus is on finding the derivative of a polynomial raised to a power, which is a common scenario in calculus.
💡Negative Exponent
A negative exponent indicates the reciprocal of the base raised to the absolute value of the exponent. In the context of the video, negative exponents are used within a polynomial function, and understanding how to handle them is important when differentiating the function. The video demonstrates that the rules for differentiating terms with negative exponents follow the same pattern as for positive exponents, but with a change in sign.
💡Rate of Change
The rate of change, or the derivative, describes how a quantity changes in response to a change in another quantity. It is a fundamental concept in calculus and is used to analyze the behavior of functions, especially in terms of their slopes at different points. In the video, the Chain Rule is used to find the derivative, which in turn allows for the calculation of the rate of change or slope of the function at any given value of x.
💡Slope
Slope refers to the steepness or gradient of a line, and in the context of functions, it represents the rate at which the function value changes with respect to the input variable. In calculus, the slope of a function at a particular point is found by calculating the derivative at that point. The video emphasizes the importance of understanding and calculating slopes using derivatives, which is a fundamental concept in analyzing the behavior of functions.
💡Composite Function
A composite function is formed by combining two or more functions in such a way that the output of one function becomes the input of another. This concept is central to the Chain Rule, as it involves differentiating a function that is made up of smaller, simpler functions. Understanding composite functions is crucial for advanced calculus topics and for solving real-world problems that involve multiple stages of change.
💡Exponent
An exponent is a mathematical notation that indicates the number of times a base is multiplied by itself. Exponents are used to express powers or multiples of a base and are fundamental in algebra and calculus. In the video, the concept of exponents is used when differentiating functions, particularly when dealing with terms raised to powers, both positive and negative.
💡Power Rule
The Power Rule is a basic rule in calculus that allows for the differentiation of functions with variables raised to a constant exponent. It states that the derivative of x^n, where n is a constant, is nx^(n-1). This rule is essential for finding derivatives of polynomial functions and is used as a building block for more complex differentiation techniques, such as the Chain Rule. The video demonstrates the use of the Power Rule when finding the derivative of terms within the larger, composite function.
💡Inner Function
In the context of composite functions, the inner function is the function that is nested or contained within another function. The Chain Rule involves differentiating the inner function first and then using its derivative as part of the process to find the derivative of the entire composite function. Understanding the concept of inner functions is crucial for applying the Chain Rule correctly and breaking down complex differentiation problems into manageable steps.
Highlights

Introduction to the chain rule with examples.

Derivative calculation of a polynomial function.

Negative exponent handling in derivatives.

Applying the chain rule to complex functions involving exponents.

Step-by-step process of finding the derivative of an inner function.

Derivative of an expression raised to a power.

Multiplying derivatives to find the derivative of a composite function.

Decrease in exponent by one when differentiating composite functions.

Derivative calculation with a function inside a larger expression.

Simplifying complex derivatives through step-by-step application of the chain rule.

Demonstration of finding the slope of a function at any point.

Handling of a more complicated function using the chain rule.

Derivative of an innermost function and its multiplication with larger expressions' derivatives.

Chain rule application to functions raised to higher powers.

Explanation of decreasing exponents in the context of the chain rule.

Encouragement for understanding the chain rule through multiple examples.

Transcripts

Browse More Related Video

The Chain Rule

Taking the derivative of two binomials using product and chain rule

Math 1325 Lecture 9 7 - Using Derivative Forumulas

Find The Derivative Using The Chain Rule

More implicit differentiation

The Chain Rule - Part 2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusChain RuleDerivativesMathematicsEducationProblem SolvingFunction AnalysisSlope CalculationAdvanced Math