❖ Integration using U-Substitution ❖
TLDRThe video script introduces the concept of U-substitution, a fundamental integration technique used to simplify complex integrals. It demonstrates the process through several examples, including integrals involving powers and trigonometric functions. The key is to identify functions that are derivatives of each other, replace them with a new variable (U), and then perform the integration. The script emphasizes the importance of reverting back to the original variable to find the antiderivative. The video also encourages viewers to explore more examples and other integration techniques on the instructor's website.
Takeaways
- 📚 U-substitution is a technique used to transform complex integrals into more recognizable forms.
- 🔄 The process involves relabeling parts of the integral and looking for expressions that are derivatives of each other.
- 🌟 Start by identifying the function to be used as U, typically something inside a parenthesis or raised to a power.
- 🎯 When applying U-substitution, take the derivative of U to find du and replace it with the corresponding expression in the integral.
- 📈 The antiderivative of U is found by applying basic integration rules, then adjust the result back to the original variable (x).
- 🌐 For example, if the integral involves x^2 + 4 raised to a power, let U = x^2 + 4 and find the antiderivative of U.
- 📊 When integrating products of trigonometric functions like sine and cosine, U-substitution can be useful as they are derivatives of each other.
- 👉 In the case of trigonometric functions, rewrite the expression to make the U-substitution clear and apply the chain rule if necessary.
- 🌿 For more complicated integrals, like x over a root of x plus a constant, U-substitution can still be applied by identifying the correct U and simplifying.
- 🔧 When the integral has a term that needs to be isolated, such as x in x + 2, use algebraic manipulation to express it in terms of U.
- 📝 Always check your work by differentiating the antiderivative to ensure it matches the original integrand.
Q & A
What is U substitution in integration?
-U substitution is an integration technique used to transform a complex integral into a more recognizable form by relabeling variables and identifying functions that are derivatives of each other.
How do you identify a suitable candidate for U substitution?
-A suitable candidate for U substitution is typically a problem where the integrand contains terms that are derivatives of each other. For example, if the integral involves a function and its derivative, it's likely that U substitution can be applied.
What is the first step in applying U substitution?
-The first step in applying U substitution is to identify the part of the integrand that can be relabeled as U and express the differential (dx) in terms of dU.
How do you perform the U substitution in the given example with 2x and x squared plus 4 raised to the 100 power?
-In the given example, we set U equal to the expression inside the parentheses, which is x squared plus 4. Then we take the derivative of U, which gives us 2x, and replace it in the integral with dU. The integral then becomes U to the 100 power times dU, which we can integrate to find the antiderivative.
What is the antiderivative of x squared plus 4 raised to the 100 power using U substitution?
-The antiderivative is (U to the 101st power) / (101) + C, where U is x squared plus 4. By substituting back, we get (x squared plus 4) to the 101st power / (101) + C.
How does U substitution work with trigonometric functions like sine and cosine?
-U substitution can be applied to trigonometric functions if they are derivatives of each other. For example, if the integral involves a product of sine and cosine functions, you can choose one of them as U and find the differential dU in terms of the other function. Then, you can integrate U and substitute back to find the antiderivative.
What is the antiderivative of cosine of theta to the fourth times sine of theta d-Theta using U substitution?
-The antiderivative is (-cosine of theta to the fifth) / (5) + C. We set U equal to cosine of theta, and after finding the differential dU as -sine of theta d-Theta, we integrate U and then substitute back to the original variables.
How does one handle a U substitution problem with a radical in the denominator, like x over the fourth root of x plus two?
-In such cases, you first rewrite the radical expression to make the power the subject of U. For x over the fourth root of x plus two, you set U equal to x plus 2, and the differential dU is 1 dx. Then, you express x in terms of U and integrate the new expression.
What is the antiderivative of x over the fourth root of x plus two?
-The antiderivative is (4/7)(x plus 2 to the 7/4) - (8/3)(x plus 2 to the 3/4) + C. This is found by setting U equal to x plus 2 and integrating U after expressing x in terms of U.
How can you verify the result of a U substitution?
-To verify the result, you can take the derivative of the antiderivative and check if it matches the original integrand. If the derivative is the same as the integrand, then the U substitution was applied correctly.
Are there more resources available for learning about U substitution?
-Yes, there are many resources available, including additional videos and examples on the speaker's website, which covers both indefinite and definite integrals involving U substitution along with other integration techniques.
Outlines
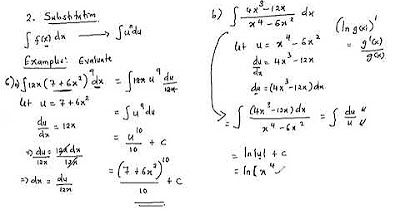
📚 Introduction to U-Substitution Integration Technique
This paragraph introduces the concept of U-substitution, an integration technique used to simplify complex integrals. The speaker explains that U-substitution involves relabeling variables to transform a complicated integral into a more recognizable form. The example provided involves integrating a function of the form [2x]x^2 + 4 raised to the 100th power. The speaker demonstrates how to identify suitable candidates for U-substitution by looking for expressions that are derivatives of each other. The process involves taking the derivative of the chosen U, substituting it back into the integral, and then solving the resulting simpler integral. The speaker emphasizes the importance of returning to the original variables at the end of the process to find the antiderivative.
📘 Applying U-Substitution to Trigonometric Functions
In this paragraph, the speaker discusses the application of U-substitution to trigonometric functions, specifically focusing on the product of cosine to the fourth power and sine of theta. The speaker identifies sine and cosine as derivatives of each other, making them suitable for U-substitution. The example involves integrating the product of these functions with respect to d-theta. The speaker shows how to set U equal to cosine of theta and then use the differential to replace the sine theta term. The integral is then solved by raising U to the fifth power, dividing by the new power, and adding a constant. Finally, the speaker substitutes back the original expression for U to find the antiderivative.
Mindmap
Keywords
💡U substitution
💡Integration
💡Derivative
💡Differential
💡Antiderivative
💡Trigonometric functions
💡Powers and exponents
💡Rewriting expressions
💡Piece-by-piece integration
💡Variable raising to a power
💡Contextualization
Highlights
Introduction to U substitution as the first integration technique learned.
The goal of U substitution is to transform a complicated integral into a more recognizable one.
An example is provided where x^2 + 4 is raised to the 100th power, and the method of U substitution is applied by relabling the inside expression as U.
The derivative relationship between U and the integral expression is key to U substitution, in this case, the derivative of x^2 + 4 leads to the 2x term.
The integral is rewritten with dU in place of dx, simplifying the process of integration.
The integration result is expressed in terms of U, and then U is replaced back with the original expression to find the antiderivative.
Another example is given with the integration of cosine^4(theta) times sine(theta) d-Theta, where U substitution is applied again.
The relationship between sine and cosine functions, being derivatives of each other, is highlighted as a clue for U substitution.
The integration process is demonstrated by raising U to the fifth power and dividing by the new power, then adding the constant C.
The method of substituting back the original expression for U to find the antiderivative is emphasized.
A third example is presented with the integration of x over the fourth root of x plus two, which also involves U substitution.
The expression x over the fourth root of x plus two is rewritten to facilitate U substitution, with U being x plus 2.
The differential dU is calculated as 1 DX, and the integral is simplified by substituting the expressions involving U.
The final integration result is obtained by replacing U back with the original expression, x plus 2, and simplifying the terms.
The video mentions that U substitution can be applied to both indefinite and definite integrals, and that more complex integration techniques exist.
The video provides a comprehensive overview of U substitution, including its application to various types of integrals and its practical use in solving complex integral problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: