2 to the x = 9, many don’t know where to start
TLDRIn this educational video, math teacher John introduces viewers to solving basic exponential equations, using the example of 2^x = 9. He explains the concept of logarithms as the inverse function of exponents, which is essential for solving such equations. John demonstrates the step-by-step process of taking the logarithm of both sides, using the property of logarithms to isolate the variable, and finally dividing by the logarithm base to find the approximate value of x, which is 3.169. He encourages viewers to practice these techniques to build their mathematical skills.
Takeaways
- 📚 The script introduces a simple exponential equation: 2^x = 9.
- 🤔 The problem might seem challenging at first, but with guidance, it's solvable even without a calculator.
- 👨🏫 John, the instructor, has decades of experience teaching middle and high school math and aims to simplify the learning process.
- 🔍 The solution to the equation involves identifying the type of equation and using appropriate mathematical tools, in this case, logarithms.
- 📈 Logarithms are used to solve exponential equations because they are inverse functions of each other.
- 🥚 The 'bacon and eggs' analogy is used to explain logarithms: log base B of A equals E, where B is the base, A is the answer, and E is the exponent.
- 📊 The process of solving the equation involves taking the logarithm of both sides and then dividing by the logarithm of the base.
- 🧮 The exact solution for x is approximately 3.169, which is found using a calculator by calculating log(9) / log(2).
- 🎓 John encourages viewers to practice math and seek clear instruction to build problem-solving skills.
- 🌐 The script promotes John's math help program and YouTube channel for further learning resources.
Q & A
What is the main topic of the video?
-The main topic of the video is solving basic exponential equations, specifically teaching how to solve the equation 2^x = 9.
Who is the speaker in the video?
-The speaker in the video is John, a teacher with decades of experience in teaching middle and high school math.
What is the approximate value of x in the equation 2^x = 9?
-The approximate value of x in the equation 2^x = 9 is 3.169.
What mathematical concept is used to solve the given exponential equation?
-Logarithms are used to solve the given exponential equation.
What is the relationship between exponential functions and logarithmic functions?
-Exponential functions and logarithmic functions are inverses of one another.
How can you express a power expression as a logarithm?
-You can express a power expression as a logarithm by using the formula log_base(b)(a) = x, where b is the base, a is the result of the power expression, and x is the exponent.
What does the logarithm button on a calculator represent?
-The logarithm button on a calculator represents the common logarithm, which is log base 10.
What is the process to solve the equation 2^x = 9 using logarithms?
-The process involves taking the logarithm of both sides of the equation, using the property of logarithms to bring the exponent x in front of the log, and then dividing the log of the result (9) by the log of the base (2) to solve for x.
What is the final step to get the approximate value of x in the equation 2^x = 9?
-The final step is to calculate log(9) divided by log(2) using a calculator, which gives the approximate value of x as 3.169.
What advice does John give to those who are struggling with math?
-John advises not to tell oneself that learning math is impossible and emphasizes the importance of clear instruction and practice to build up skills in solving various types of math problems.
Where can viewers find more information on math if they are interested?
-Viewers can find more information on math by checking out John's math health program at tcmathacademy.com and his YouTube channel, which has a variety of videos on different math topics.
Outlines
📚 Introduction to Solving Exponential Equations
The video begins with an introduction to solving a simple exponential equation, 2^x = 9. The speaker, John, a math teacher with decades of experience, offers to guide viewers through the solution step by step. He encourages viewers to attempt the problem and share their answers in the comments. John then provides the approximate solution, x ≈ 3.169, and explains the concept of approximation in mathematics. He also introduces himself and promotes his math health program for further assistance in learning math.
🧠 Understanding Exponential Equations and Logarithms
John explains the difference between exponential and quadratic equations, emphasizing that the unknown variable x is in the exponent position in the given equation. He introduces logarithms as the solution tool for exponential equations, highlighting their inverse relationship with exponential functions. John simplifies the concept of logarithms using a catchy phrase 'bacon and eggs' to represent log base 2, and explains how to convert an exponential expression into a logarithmic one. He also mentions the availability of his algebra and pre-calculus courses for further learning.
🔢 Practical Steps for Solving the Given Exponential Equation
The speaker walks through the practical steps to solve the exponential equation 2^x = 9 using logarithms. He explains the process of taking the logarithm of both sides of the equation and using the property of logarithms to isolate the variable x. John then demonstrates how to solve for x by dividing the logarithm of 9 by the logarithm of 2, resulting in the approximate value of x ≈ 3.169. He emphasizes the importance of understanding the process rather than just the final answer.
🌟 Encouragement for Continued Learning in Mathematics
John concludes the video by encouraging viewers to embrace the challenge of learning math, regardless of their current level. He assures that with great instruction and practice, anyone can master mathematical concepts, even as they become more complex in advanced courses like calculus. He invites viewers to engage with his YouTube channel and other resources for more math tutorials, wishing everyone success in their mathematical journey.
Mindmap
Keywords
💡Exponential Equation
💡Logarithm
💡Base
💡Exponent
💡Solving Equations
💡Calculator
💡Algebra
💡Mathematics Instruction
💡Logarithmic Expression
💡Mathematics Adventure
💡YouTube Math Man
Highlights
The video introduces a method to solve a basic exponential equation, making complex math more accessible.
The equation presented is 2^x = 9, and the goal is to solve for x.
The correct solution for x is approximately 3.169, showcasing the use of approximation in math.
The video emphasizes the need for a calculator to solve this type of problem.
John, the instructor, has decades of experience teaching middle and high school math.
The video provides a link to John's math help program at tcmathacademy.com.
The difference between the exponent location in 2^x = 9 and x^2 = 9 is explained, highlighting the concept of an exponential equation.
The video touches on the importance of understanding different types of equations in algebra.
Logarithms are introduced as a tool to solve exponential equations, as they are inverse functions to each other.
A simple explanation of logarithms is given using the 'bacon and eggs' analogy.
The process of solving the exponential equation 2^x = 9 is walkthrough step by step.
The use of logarithms is demonstrated by taking the logarithm of both sides of the equation.
The property of logarithms to move the exponent in front of the log is utilized in the solution process.
The final algebraic step to solve for x is to divide both sides of the equation by the logarithm base.
The video encourages viewers to practice math problems to build their skills, not just watch solutions.
John's passion for teaching math is emphasized, aiming to make learning math as easy as possible.
The video concludes with a positive message, encouraging viewers to continue learning math regardless of their current level.
Transcripts
Browse More Related Video

6 to the (3x + 5) = 1, many don’t know where to start
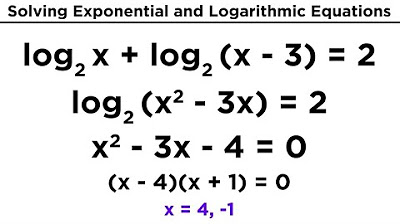
Solving Exponential and Logarithmic Equations
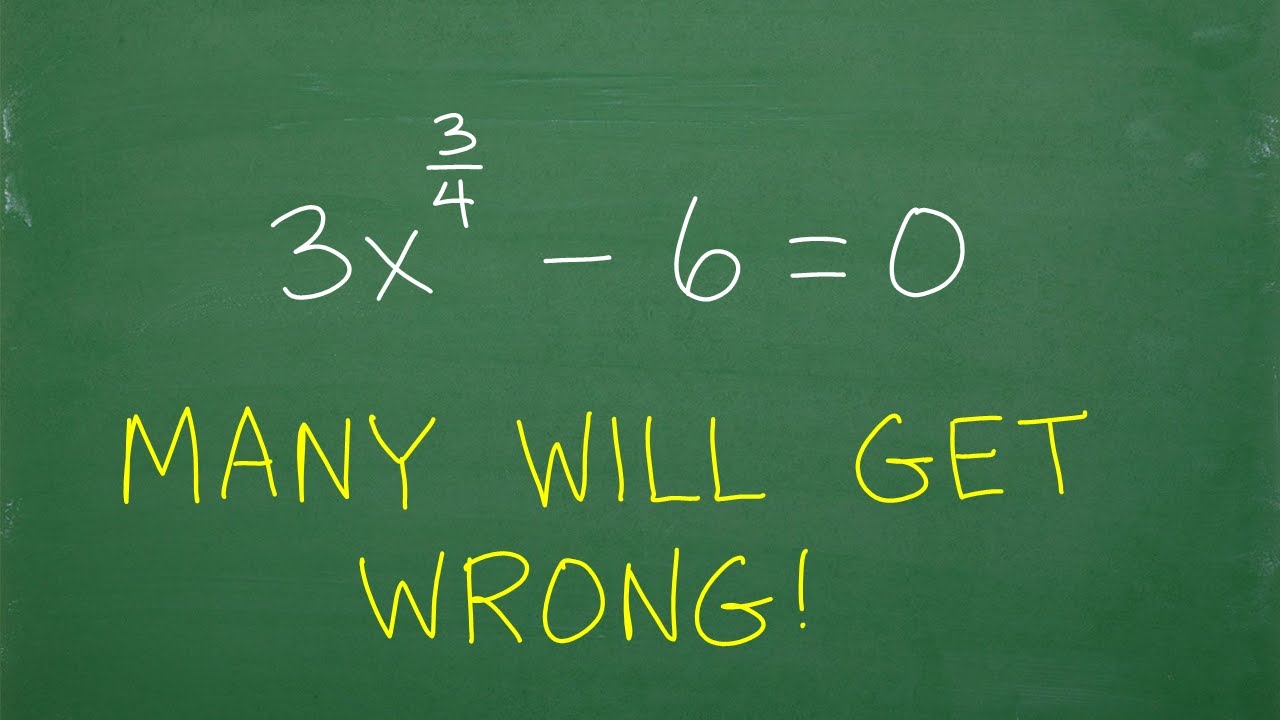
3x to the (3/4) power – 6 = 0, Many don’t know where to start…
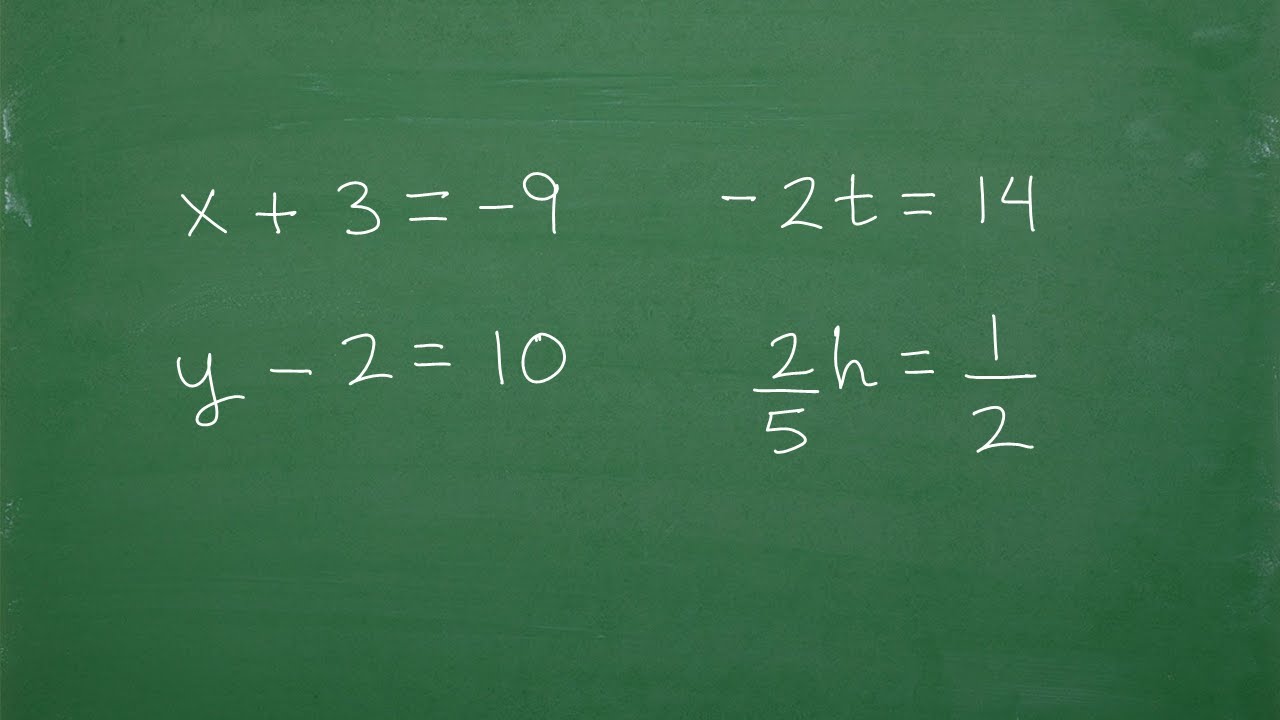
Let’s Solve These Basic Algebra Equations- Step-by-Step…….

How To Solve Exponential Equation x^5=9^x || Solving Exponential Equations.

Unit V: Lec 1 | MIT Calculus Revisited: Single Variable Calculus
5.0 / 5 (0 votes)
Thanks for rating: