Potential and Kinetic Energy
TLDRIn this informative talk, Mr. Andersen explores the concepts of potential and kinetic energy, emphasizing their roles in the conservation of energy. He explains potential energy as mgh (mass times gravitational acceleration times height) and kinetic energy as 1/2 mv^2 (mass times velocity squared), using a pendulum as a practical example of energy transformation. He also calculates the potential energy at the top of a ten-story building and compares the kinetic energy of a casual pitch to that of a major league fastball, highlighting the significance of velocity in energy calculations.
Takeaways
- 🌟 Energy is the ability to do work and is measured in joules.
- 📈 Work is calculated as force times distance.
- 🔄 The law of conservation of energy states that energy cannot be created or destroyed, only converted.
- ⚖️ Energy can be converted into mass, as described by E=mc².
- 🏋️ Potential energy is due to an object's position and is calculated as mgh (mass times gravitational acceleration times height).
- 🏃♂️ Kinetic energy is due to an object's motion and is calculated as 1/2 mv² (half of mass times velocity squared).
- 🔄 In a pendulum, energy is continuously converted from potential to kinetic and vice versa.
- 📉 Friction, heat, and sound cause energy loss over time, preventing perpetual motion.
- 🏢 An example of potential energy calculation: A person at the top of a ten-story building has 2.4 x 10^4 joules of energy.
- ⚾️ The kinetic energy of a baseball pitch depends on the mass of the ball and the velocity of the pitch, with a major league pitch having 150 joules.
- 🏆 The importance of the squaring of velocity in the kinetic energy equation, as it significantly affects the amount of energy.
Q & A
What is the definition of energy?
-Energy is the ability to do work, and it is measured in joules.
What does the law of conservation of energy state?
-The law of conservation of energy states that energy can neither be created nor destroyed, only converted from one form to another.
How can energy be converted according to E=mc^2?
-According to E=mc^2, energy can be converted into mass, where E is the energy, m is the mass, and c is the speed of light.
What are the two main forms of energy discussed in the script?
-The two main forms of energy discussed are potential energy and kinetic energy.
What is potential energy?
-Potential energy is the energy due to an object's position, such as gravitational potential energy, and it is calculated as mgh (mass times gravitational acceleration times height).
What is kinetic energy?
-Kinetic energy is the energy due to an object's motion, and it is calculated as 1/2 mv^2 (half of the mass times the velocity squared).
How does a pendulum demonstrate the conversion of potential to kinetic energy?
-In a pendulum, potential energy is highest at the top when the pendulum is still, and as it swings down, this potential energy is converted into kinetic energy. The energy oscillates between potential and kinetic as the pendulum moves back and forth.
What factors contribute to the loss of energy in a pendulum?
-The loss of energy in a pendulum is due to friction, heat, and sound as it moves.
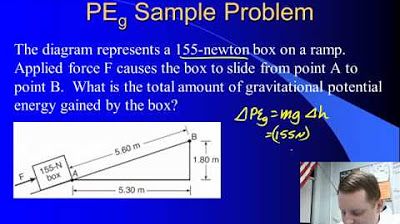
How can the potential energy of a ten-story building be calculated?
-The potential energy can be calculated using the formula mgh, where m is the mass (78 kg), g is the gravitational acceleration (9.81 m/s^2), and h is the height (32 m), resulting in 24,485.76 joules or approximately 2.4 x 10^4 joules.
What is the kinetic energy of a baseball thrown at 20 miles per hour?
-The kinetic energy of a baseball (mass 0.145 kg) thrown at 20 miles per hour (9.0 m/s) is 5.9 joules, calculated using the formula 1/2 mv^2.
How does the kinetic energy of a major league pitcher's throw compare to a regular throw?
-A major league pitcher throwing a baseball at 100 miles per hour (45 m/s) has a kinetic energy of 150 joules, which is roughly 25 times more than a regular throw at 20 miles per hour (5.9 joules), highlighting the importance of the velocity squared in the kinetic energy equation.
Outlines
🌟 Introduction to Energy Concepts
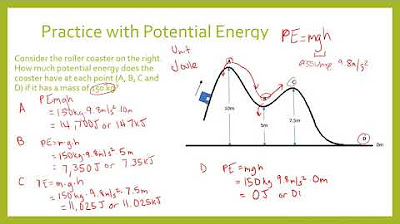
This paragraph introduces the fundamental concepts of potential and kinetic energy. Mr. Andersen explains that energy, defined as the ability to do work, is measured in joules and is subject to the law of conservation, meaning it cannot be created or destroyed, only converted. He differentiates between potential energy, which is due to an object's position (specifically potential gravitational energy and chemical potential energy), and kinetic energy, which is due to motion. The equations for calculating potential energy (mgh) and kinetic energy (1/2mv^2) are provided, with m representing mass, g gravitational acceleration, h height, and v velocity. The conversion of energy from potential to kinetic and vice versa is illustrated using the example of a pendulum.
📈 Calculation of Potential and Kinetic Energy
In this paragraph, Mr. Andersen delves into the practical application of the equations for potential and kinetic energy through examples. He first calculates his own potential energy at the top of a ten-story building, using his mass, the acceleration due to gravity, and the building's height to得出 24,485.76 joules, which he rounds to 2.4 x 10^4 joules. Then, he discusses the concept of kinetic energy in the context of pitching a baseball, comparing the energy involved in a throw at 20 miles per hour to that of a major league pitcher throwing at 100 miles per hour. By using the mass of the baseball and the respective velocities, he calculates the kinetic energy for both scenarios: 5.9 joules for his throw and 150 joules for the major league pitch, emphasizing the significance of the squared velocity in the kinetic energy equation.
Mindmap
Keywords
💡Energy
💡Work
💡Conservation of Energy
💡Potential Energy
💡Kinetic Energy
💡Pendulum
💡Gravitational Acceleration
💡Velocity
💡Friction
💡Significant Digits
💡Conversion of Energy
Highlights
Energy is the ability to do work, and work is defined as a force times distance, measured in joules.
The law of conservation of energy states that energy cannot be created or destroyed, only converted.
Energy can be converted into mass as described by the equation E=mc^2.
Potential energy is related to an object's position and is calculated as mgh (mass times gravitational acceleration times height).
Kinetic energy is associated with an object's motion and is calculated as 1/2 mv^2 (half of mass times velocity squared).
A pendulum demonstrates the conversion of potential energy to kinetic energy and vice versa as it swings.
At the highest point of a pendulum's swing, all the energy is potential; at the lowest point, it's all kinetic.
Friction, heat, and sound cause the eventual loss of a pendulum's energy, leading to its stop.
The potential energy of a person at the top of a ten-story building can be calculated using mgh, resulting in 2.4 x 10^4 joules for a 78 kg person.
Kinetic energy depends on the velocity of an object, with the velocity being squared in the equation, making it very significant.
A baseball thrown at 20 miles per hour has 5.9 joules of kinetic energy, while one thrown at 100 miles per hour has 150 joules.
The velocity of a thrown baseball has a squared effect on its kinetic energy, meaning a fivefold increase in speed results in a twenty-fivefold increase in energy.
Understanding the equations for potential and kinetic energy allows for solving complex problems involving energy conversion.
The concept of energy conversion is applicable in various scenarios, such as calculating how high a sprinter could pole vault based on their kinetic energy.
The essence of the discussion is the measurement of energy in joules and its conversion from potential due to position to kinetic due to motion.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: