ANOVA Part IV: Bonferroni Correction | Statistics Tutorial #28 | MarinStatsLectures

MarinStatsLectures-R Programming & Statistics
15 Oct 201816:55
EducationalLearning
32 Likes 10 Comments

TLDRThis transcript discusses the concept of multiple comparisons and the associated increase in type 1 error rate when conducting more than one test. It uses the context of one-way ANOVA to explain the need for corrections like Bonferroni's method, which adjusts the alpha level per test to control the overall error rate. The example of weight loss across different diets illustrates the process of pairwise comparisons and the interpretation of confidence intervals to identify significant differences between groups. The transcript emphasizes understanding the concepts over calculations, the difference between statistical and clinical significance, and the trade-off between type 1 and type 2 errors.

Takeaways
  • 🧠 The concept of multiple comparisons is introduced to address the increase in Type 1 error rate when conducting more than one test or comparison.
  • 📈 In the context of one-way ANOVA, the F statistic is used to determine if at least one mean differs significantly among the groups.
  • 🔄 Pairwise comparisons are performed to identify which specific means differ from each other after rejecting the null hypothesis in ANOVA.
  • 🎯 The probability of making at least one Type 1 error increases with the number of tests conducted, leading to the need for corrections like the Bonferroni method.
  • 🔢 Bonferroni's correction adjusts the alpha level by dividing the desired overall Type 1 error rate by the number of comparisons to control the familywise error rate.
  • 📊 Each pairwise comparison uses an adjusted confidence level to maintain the overall Type 1 error rate at a specified level, such as 5%.
  • 🚫 The independence assumption between pairwise comparisons simplifies calculations and is generally more conservative.
  • 📉 The use of Bonferroni's correction reduces the chance of making at least one Type 1 error, but it also increases the Type 2 error rate (false negatives).
  • 🤔 The statistical significance of a result does not necessarily equate to clinical or scientific significance, and the context and effect size must be considered.
  • 🏃‍♂️ An analogy of runners in a 10km race illustrates the concept of statistical significance and the importance of the magnitude of differences.
  • 📋 The focus should be on understanding the concepts and interpretations rather than the exact calculations, which can be performed by statistical software.
Q & A

  • What is the main issue with conducting multiple tests or comparisons simultaneously?

    -The main issue with conducting multiple tests or comparisons simultaneously is that the Type 1 error rate increases. This means there is a higher chance of making a false positive, or incorrectly rejecting the null hypothesis.

  • What is the concept of Type 1 error and how does it relate to the alpha level?

    -A Type 1 error occurs when you reject the null hypothesis when it is actually true. The alpha level represents the probability of making a Type 1 error. For example, an alpha of 5% means there is a 5% chance of making a Type 1 error in any given test.

  • How does the probability of making at least one Type 1 error change with multiple tests?

    -The probability of making at least one Type 1 error increases with the number of tests conducted. For instance, if each test has a 5% chance of a Type 1 error, the combined probability for multiple tests can be calculated using the formula 1 - (1 - alpha)^n, where n is the number of tests.

  • What is Bonferroni's multiple testing correction, and how does it work?

    -Bonferroni's multiple testing correction is a method to control the familywise error rate, which is the probability of making at least one Type 1 error across all tests. It works by dividing the desired overall alpha level by the number of comparisons, thus adjusting the alpha level for each individual test to keep the overall error rate at the desired level.

  • What is the adjusted alpha level for Bonferroni's correction in the context of six pairwise comparisons?

    -For six pairwise comparisons, the adjusted alpha level using Bonferroni's correction would be 0.05 (the desired overall alpha level) divided by 6 (the number of comparisons), resulting in an adjusted alpha of 0.00833 or 0.83%.

  • How does the confidence level change when applying Bonferroni's correction?

    -When applying Bonferroni's correction, the confidence level for each individual test or confidence interval is adjusted. Instead of the typical 95% confidence level, you would use a higher confidence level to maintain the desired overall alpha level. For example, with an adjusted alpha of 0.00833, the confidence level would be approximately 99.167%.

  • What is the relationship between statistical significance and clinical or scientific significance?

    -Statistical significance indicates that there is a low probability that the observed results occurred by chance alone. However, clinical or scientific significance refers to the practical importance or meaningfulness of the results in the real world. A statistically significant result may not always be clinically or scientifically meaningful, and vice versa.

  • What is the trade-off between Type 1 and Type 2 error rates?

    -The trade-off between Type 1 and Type 2 error rates is that reducing one increases the other. Lowering the Type 1 error rate (false positives) by using a more stringent alpha level will result in an increased Type 2 error rate (false negatives), and vice versa.

  • How can the concept of multiple comparisons be applied in the context of a one-way ANOVA?

    -In the context of a one-way ANOVA, after finding a significant F-statistic indicating that at least one group mean differs from the others, multiple comparisons are used to determine which specific group means are different. This involves conducting pairwise comparisons between all groups and applying a correction for multiple comparisons to control the overall Type 1 error rate.

  • What is the difference between familywise error rate and the concept of individual alpha levels?

    -The familywise error rate is the probability of making at least one Type 1 error across all tests or comparisons. In contrast, the individual alpha level is the probability of making a Type 1 error for a single test. Multiple testing corrections like Bonferroni's adjustment are designed to control the familywise error rate by adjusting the individual alpha levels for each test.

  • Why is it important to focus on concepts rather than specific calculations or formulas when learning about multiple comparisons?

    -Focusing on concepts is important because it helps in understanding the underlying principles and logic behind multiple comparisons and error rate control. While specific calculations and formulas can be performed by software, grasping the concepts allows for better interpretation of results and more informed decision-making in statistical analysis.

Outlines
00:00
🔍 Introduction to Multiple Comparisons and Corrections

This paragraph introduces the concept of multiple comparisons and the need for corrections when performing more than one test or comparison. It explains how the type 1 error rate increases with the number of tests conducted, using the context of one-way analysis of variance (ANOVA) as an example. The paragraph discusses the risk of making at least one type 1 error when conducting multiple tests and sets the stage for learning how to control this error rate. It also introduces the idea of pairwise comparisons to identify which means differ significantly from others.

05:01
🧐 Understanding Type 1 Error Rates and Bonferroni Correction

This paragraph delves into the probability of making type 1 errors in multiple testing scenarios. It explains how the probability of making at least one type 1 error can be calculated and demonstrates that this probability increases with the number of tests. The paragraph then introduces Bonferroni's multiple testing correction as a method to control the overall type 1 error rate. It explains the concept of adjusting the alpha level for each individual test based on the number of comparisons, thereby reducing the likelihood of committing type 1 errors.

10:07
📊 Analyzing Pairwise Comparisons and Interpreting Results

The focus of this paragraph is on analyzing pairwise comparisons and interpreting the results. It describes how to use confidence intervals to compare different groups and determine if the differences between means are statistically significant. The paragraph uses an example to illustrate that not all significant differences are clinically or scientifically meaningful, emphasizing the importance of considering effect size and context. It also discusses the limitations of the Bonferroni correction and the potential for increased type 2 errors when controlling type 1 errors.

15:07
🚨 Key Reminders in Multiple Testing Corrections

This paragraph concludes the discussion on multiple testing corrections with important reminders. It highlights the distinction between statistical significance and real-world meaningfulness, the trade-off between type 1 and type 2 error rates, and the practicality of using software for calculations. The paragraph also reminds viewers that while Bonferroni's correction is discussed, there are many other methods available for multiple testing corrections, all sharing a similar conceptual framework with minor mechanical differences.

Mindmap
Keywords
💡Multiple Comparisons
Multiple comparisons refer to the process of conducting more than one statistical test or comparison simultaneously. In the context of the video, this concept is crucial when performing a one-way analysis of variance (ANOVA), where the goal is to compare the means of multiple groups. As the number of comparisons increases, so does the risk of committing a Type 1 error, which is a false positive result indicating a significant difference when there is none.
💡Type 1 Error
A Type 1 error occurs when a statistical test incorrectly rejects a true null hypothesis, leading to a false positive result. In other words, it is the mistake of finding a significant difference when, in reality, there is none. The video emphasizes the importance of controlling the Type 1 error rate, especially when performing multiple comparisons, as the likelihood of committing this error increases with the number of tests conducted.
💡Alpha Level
The alpha level, often set at 5%, is the probability threshold for determining statistical significance in a test. It represents the maximum acceptable chance of making a Type 1 error. In the video, the alpha level is discussed in relation to multiple comparisons, where it is adjusted using methods like the Bonferroni correction to control the overall Type 1 error rate when conducting multiple tests.
💡Bonferroni Correction
The Bonferroni correction is a statistical method used to adjust the alpha level in order to control the familywise error rate when performing multiple comparisons. By dividing the desired overall alpha level by the number of comparisons, a new, lower alpha level is established for each individual test. This adjustment helps to reduce the likelihood of committing Type 1 errors as the number of tests increases.
💡Familywise Error Rate (FWER)
The familywise error rate, or FWER, is the probability of making at least one Type 1 error in a set of statistical tests performed simultaneously. It is a measure used to control the overall error rate when multiple comparisons are conducted. The goal is to keep the FWER at a predetermined level, such as 5%, to ensure that the likelihood of committing any Type 1 errors across all tests remains low.
💡One-Way ANOVA
One-way ANOVA, or analysis of variance, is a statistical method used to compare the means of three or more independent groups. It tests the null hypothesis that all group means are equal against the alternative hypothesis that at least one group mean differs from the others. The video uses one-way ANOVA to set the stage for discussing multiple comparisons, as it is a common procedure where the issue of multiple comparisons arises.
💡Pairwise Comparisons
Pairwise comparisons involve comparing each pair of groups or treatments in a set of multiple groups. In the context of the video, after conducting a one-way ANOVA and finding evidence for at least one mean difference, pairwise comparisons are performed to identify which specific groups differ from each other. These comparisons are done using methods like independent two-sample t-tests or confidence intervals.
💡Confidence Intervals
Confidence intervals are a statistical measure that provides a range of values within which the true population parameter, such as a mean, is likely to fall with a certain level of confidence. They are used in hypothesis testing and estimation to convey uncertainty about the parameter estimate. In the video, confidence intervals are used in pairwise comparisons to assess whether the difference between two group means is statistically significant.
💡Statistical Significance
Statistical significance refers to the probability that the observed results are not due to chance alone. It is a measure used to determine if there is a significant difference between groups or treatments based on the p-value and the chosen alpha level. However, statistical significance does not necessarily imply practical or scientific significance, as the effect size and context must also be considered.
💡Type 2 Error
A Type 2 error occurs when a statistical test fails to reject a false null hypothesis, leading to a false negative result. This means that the test concludes there is no significant difference when, in fact, there is. When controlling for Type 1 errors by lowering the alpha level, the risk of making a Type 2 error increases, as the test becomes more conservative and less likely to detect a true effect.
💡Effect Size
Effect size is a measure that quantifies the magnitude of a difference or relationship between variables in a study. It provides an indication of how meaningful or important the observed effect is, beyond just statistical significance. Effect size is crucial for interpreting the practical significance of research findings, as it helps to assess whether the observed differences are large enough to be of consequence.
Highlights

The discussion revolves around the concept of multiple comparisons and the need for corrections in statistical analysis.

The type 1 error rate increases with the number of tests conducted, which is a critical issue in multiple testing scenarios.

The example used in the transcript involves comparing weight loss across four different diets using a one-way ANOVA.

The F statistic is calculated as a ratio of variability explained by diet to variability not explained by diet.

A test statistic of 6.1 with a p-value of 0.0011 led to the rejection of the null hypothesis, suggesting at least one mean differs from the rest.

Pairwise comparisons are conducted to identify which diets significantly differ from one another.

The mathematical approach to pairwise comparisons involves selecting two groups from four, resulting in six possible combinations.

The use of independent two-sample t-tests for each pairwise comparison is discussed, including the calculation of confidence intervals and test statistics.

The probability of making at least one type 1 error across six tests is approximately 26.5% without correction.

Bonferroni's multiple testing correction is introduced as a method to control the familywise error rate.

Bonferroni's correction involves using an adjusted alpha level divided by the number of comparisons, resulting in a lower overall type 1 error rate.

The adjusted alpha level for each individual test after Bonferroni's correction is 0.00833, with 99.167% confidence.

The application of Bonferroni's correction reduces the probability of making at least one type 1 error to around 4.9%.

The transcript emphasizes the importance of understanding the concepts behind statistical methods rather than focusing on the calculations.

Statistical significance does not necessarily equate to clinical or scientific significance, and the context must be considered.

There is a trade-off between type 1 and type 2 error rates, with lower false positives coming at the expense of increased false negatives.

Software is typically used for calculations, and the focus should be on understanding the concepts and what the software is doing.

Multiple testing corrections are available, with Bonferroni's being one of the simplest to understand, and others varying slightly in mechanics.

Transcripts

Browse More Related Video

Bonferroni's Method for Pairwise Multiple Comparisons

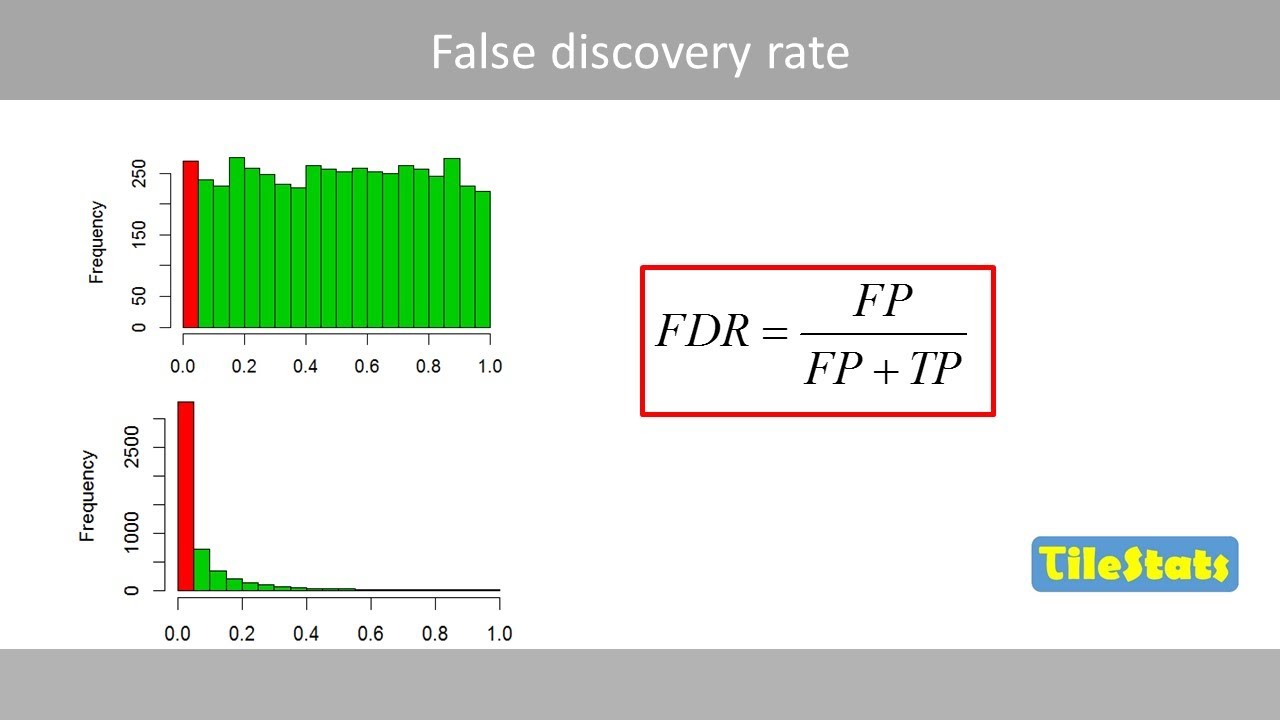
False discovery rate (FDR) - explained | vs FWER

The Problem of Multiple Comparisons | NEJM Evidence

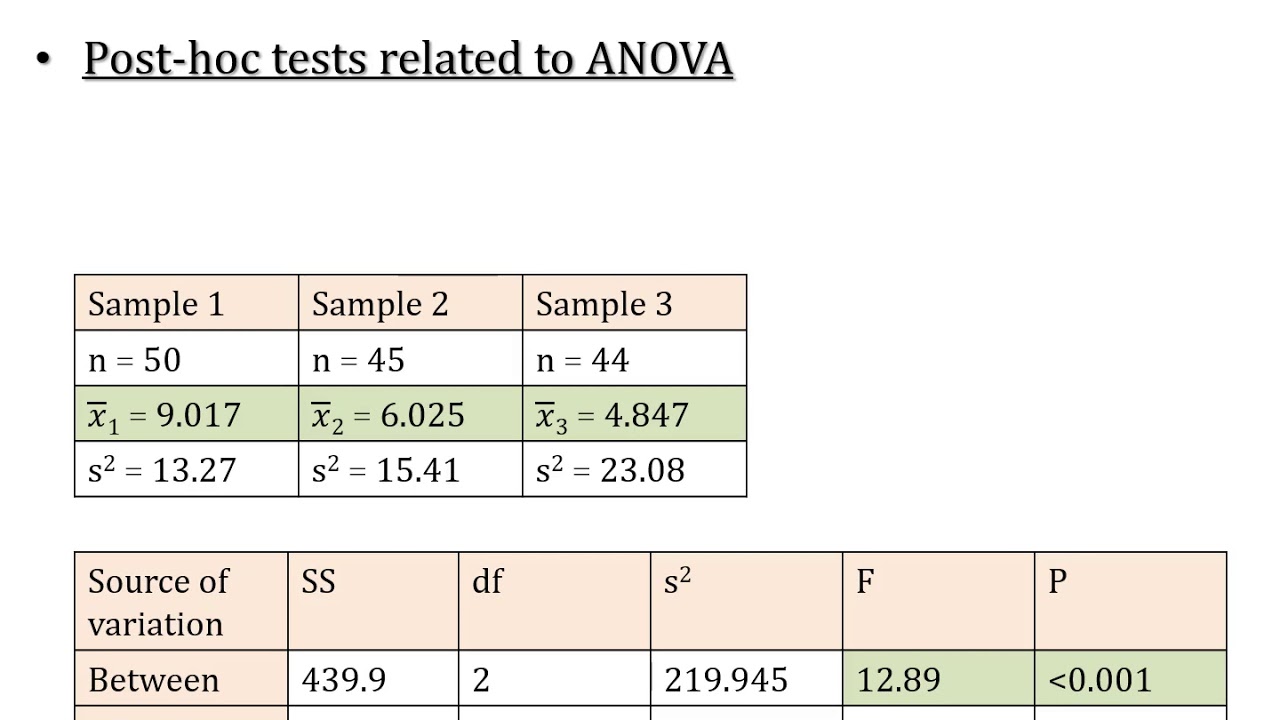
LSD; Least Significant Difference; Post Hoc Test of ANOVA; Comparison of Means (Part A)

Errors and Power in Hypothesis Testing | Statistics Tutorial #16 | MarinStatsLectures

Null Hypothesis, p-Value, Statistical Significance, Type 1 Error and Type 2 Error

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MultipleComparisonsType1ErrorBonferroniCorrectionStatisticalAnalysisErrorControlANOVAHypothesisTestingDataInterpretationSignificanceTestingStatisticalSignificance