AP Physics C: Kinematics Review (Mechanics)
TLDRIn this comprehensive review of AP Physics C: Mechanics, the focus is on key concepts such as kinematics, vectors versus scalars, uniformly accelerated motion (UAM), free fall, component vectors, unit vectors, and projectile motion. The discussion emphasizes the importance of understanding units, the difference between average and instantaneous quantities, and the application of UAM equations. The review also clarifies the use of component vectors and unit vectors in vector addition, and illustrates the concept of relative velocity and projectile motion, providing a solid foundation for tackling dynamics and further physics problems.
Takeaways
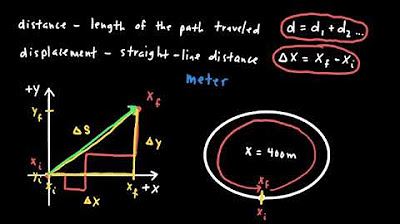
- 📚 Kinematics is the starting point of the AP Physics C: Mechanics curriculum, focusing on the motion of objects without considering the forces that cause the motion.
- 🔢 Units are crucial in physics; every numerical answer must be accompanied by its appropriate units, except for dimensionless ratios like the coefficient of friction (Mu).
- 🧮 Conversion of units is a fundamental skill, demonstrated by converting the density of krypton from grams per centimeter cubed to kilograms per meter cubed.
- 📐 Vectors and scalars differ in that vectors have both magnitude and direction, while scalars have only magnitude.
- 🌟 Momentum is a vector quantity, and it's essential to consider both its x and y components when solving conservation of momentum problems.
- 📈 Velocity is defined by two types: average velocity (change in position over change in time) and instantaneous velocity (the derivative of position with respect to time).
- 🚀 Uniformly Accelerated Motion (UAM) occurs when an object experiences a constant acceleration, and there are five UAM variables and four UAM equations that describe such motion.
- 🎢 Free fall is a specific case of UAM where an object is acted upon solely by gravity, resulting in a constant acceleration of -9.81 m/s² downward.
- 📊 Graphs for free fall motion show a constant acceleration as a horizontal line, a linear increase in velocity with a constant negative slope, and a concave down position graph that starts above the x-axis and crosses it as time progresses.
- 🔄 Component vectors represent the individual x, y, and z components of a vector, which can be determined using trigonometric relationships like SOH CAH TOA.
- 🪐 Unit vectors (i, j, k) simplify vector addition by allowing the direct summation of vectors along their respective axes, and they are essential for identifying positions in multi-dimensional space.
Q & A
Why is it important to remember units in physics calculations?
-It is crucial to remember units in physics calculations to ensure accuracy and clarity in the results. Units provide a standard for measurement and help in understanding the scale and context of the answer. Without units, a numerical answer might not convey the correct magnitude or dimension of the physical quantity being measured.
What mistake did Bobby make when converting the density of krypton gas?
-Bobby forgot to cube the conversion factor when converting the density of krypton gas from grams per centimeter cubed to kilograms per meter cubed, leading to an incorrect answer. The correct process involves cubing the conversion factor to ensure that the units of volume (cubed units) are correctly converted.
What distinguishes a vector from a scalar?
-A vector is distinguished from a scalar by having both magnitude and direction, whereas a scalar has magnitude only. This difference is significant because it affects how these quantities are used in physics equations and problems, especially in fields like mechanics and electromagnetism.
How do average velocity and instantaneous velocity differ?
-Average velocity is calculated as the change in position over change in time for a given time period, while instantaneous velocity is the derivative of position with respect to time, representing the velocity at a specific moment. This distinction is important for understanding motion over different time scales.
What are the conditions for using Uniformly Accelerated Motion (UAM) equations?
-UAM equations can be used when the acceleration of the object is constant (uniform) over time. This means that the acceleration must be a fixed number, not a function that varies with time or position, allowing for simplified motion analysis under these specific conditions.
How can students determine the final velocity of an object using UAM equations?
-Students can determine the final velocity of an object using UAM equations by applying the correct formula that relates initial velocity, acceleration, and time. This involves understanding and correctly manipulating the equations to solve for the final velocity, given the other variables.
Why is free fall considered a type of Uniformly Accelerated Motion?
-Free fall is considered a type of Uniformly Accelerated Motion because the only force acting on the object is gravity, which provides a constant acceleration towards the Earth. This constant acceleration (negative 9.81 meters per second squared on Earth) fits the criteria for UAM.
How do component vectors relate to the original vector they represent?
-Component vectors are vectors in the x, y, and possibly z directions that, when added together vectorially, result in the original vector. This concept is crucial for breaking down vectors into more manageable components for analysis in physics problems.
What is the significance of unit vectors in physics?
-Unit vectors, denoted with a hat symbol over i, j, and k, are significant because they provide a way to express vectors in a standardized form with a magnitude of one. They simplify vector addition and analysis by clearly defining direction in one, two, or three-dimensional space.
How does the concept of relative velocity apply to motion in physics?
-The concept of relative velocity is used to describe the velocity of an object in relation to another reference frame, taking into account both objects' movements. It is essential for solving problems involving multiple velocities, such as determining the necessary direction to counteract wind effects on an airplane.
Outlines
📚 Kinematics Review: Units, Conversions, and Vectors
The paragraph begins with a review of the AP Physics C: Mechanics Curriculum, focusing on kinematics. It emphasizes the importance of remembering units for all measurements and the necessity of performing unit conversions, as demonstrated by the incorrect conversion of krypton's density by a student, Bobby. The discussion then moves to the distinction between vectors and scalars, highlighting the significance of this difference in physics exams. The conversation clarifies that vectors have both magnitude and direction, while scalars have only magnitude. The concept of momentum as a vector and the common mistake of omitting direction components in problem-solving are also addressed. The paragraph concludes with an explanation of average and instantaneous velocity and acceleration, and introduces the concept of Uniformly Accelerated Motion (UAM), discussing its variables and equations.
📈 UAM Equations and Free Fall
This paragraph delves deeper into Uniformly Accelerated Motion (UAM), explaining the conditions under which UAM equations apply and the variables involved. It corrects a common mistake students make regarding the number of UAM equations and variables, and emphasizes the importance of understanding the difference between the equations taught in class and those provided on the AP exam equation sheet. The concept of free fall is introduced as a specific case of UAM, where the only force acting is gravity, leading to a constant acceleration equal to the acceleration due to gravity. The paragraph also covers the graphical representations of position, velocity, and acceleration for an object in free fall, providing a step-by-step explanation of how these graphs would appear over time.
📐 Component Vectors and Unit Vectors
The focus of this paragraph is on component vectors and unit vectors. It starts with a practical example of determining the component vectors of an acceleration vector at a given angle, using trigonometric functions. The paragraph explains the process of breaking down a vector into its x and y components using SOH CAH TOA. It then introduces unit vectors i, j, and k, which simplify vector addition by allowing the direct combination of vectors along the x, y, and z axes. The use of unit vectors in identifying an object's position in multi-dimensional space is also discussed. The paragraph concludes with a brief mention of relative velocity and projectile motion, setting the stage for further discussion in the next paragraph.
🚀 Projectile Motion and Review Conclusion
The final paragraph of the script discusses the general strategy for solving projectile motion problems, emphasizing the separation of known values by direction due to the different forces acting on the object in the x and y directions. It outlines the constant velocity in the x direction and free fall acceleration in the y direction as key aspects of projectile motion. The paragraph also touches on the importance of breaking down the initial velocity into its components. The review concludes with a brief mention of the next topics to be covered, including Newton's laws and dynamics, and directs students to additional resources for further study.
🙌 Thank You and Learning
This brief paragraph serves as a closing remark, expressing gratitude for the students' participation in the learning session. It acknowledges the shared learning experience and encourages continued engagement with the material.
Mindmap
Keywords
💡Kinematics
💡Units and Conversions
💡Vectors vs Scalars
💡Instantaneous Velocity
💡Uniformly Accelerated Motion (UAM)
💡Free Fall
💡Component Vectors
💡Unit Vectors
💡Relative Velocity
💡Projectile Motion
Highlights
Review of the entire AP Physics C: Mechanics Curriculum begins with kinematics.
Students must remember units for all measurements and identify every numerical answer with units.
Bobby correctly converts the density of krypton gas from grams per centimeter cubed to kilograms per meter cubed.
The distinction between vectors, which have magnitude and direction, and scalars, which only have magnitude.
Momentum is a vector, and it's crucial to include both x and y directions in conservation of momentum problems.
The equation for average velocity is the change in position over change in time, while instantaneous velocity is the derivative of position with respect to time.
The difference between average and instantaneous velocity lies in that average is over a time period and instantaneous is at a specific point in time.
Uniformly Accelerated Motion (UAM) equations apply when the acceleration is constant, not changing as a function of time or position.
The five UAM variables are acceleration, final velocity, initial velocity, displacement, and change in time.
There are four UAM equations provided on the AP exam equation sheet, which are essential for solving related physics problems.
Free fall is an example of uniformly accelerated motion with a constant acceleration equal to the negative gravitational acceleration.
In free fall, the acceleration in the y direction is negative 9.81 meters per second squared, directed downwards.
Component vectors are the individual vectors in the x, y, and z directions that combine to form the original vector.
Unit vectors i, j, and k have a magnitude of one in the x, y, and z directions, respectively, simplifying vector addition.
Relative velocity is calculated using vector addition, which is particularly useful in scenarios like flying a plane into the wind.
Projectile motion involves an object moving in both the x and y directions, subject only to gravity in the y direction.
The general strategy for solving projectile motion problems involves separating the known values by direction and using the appropriate equations for each.
The review concludes with a mention of the next topic: dynamics, including Newton's three laws, forces, and equilibrium.
Transcripts
Browse More Related Video
AP Physics 1 Kinematics Review

AP Physics 1: Kinematics Review

AP Physics C: Rotational Kinematics Review (Mechanics)

Physics 1 Formulas and Equations - Kinematics, Projectile Motion, Force, Work, Energy, Power, Moment

2022 Live Review 1 | AP Physics C: Mechanics | One- and Two-Dimensional Kinematics

Scalars, Vectors, and Vector Operations
5.0 / 5 (0 votes)
Thanks for rating: