Biostatistics - Evaluation of Diagnostic Tests: Sensitivity & Specificity
TLDRThis video script introduces a new series on biostatistics, focusing on the evaluation of diagnostic tests through sensitivity and specificity. Sensitivity is defined as the proportion of correct positive results among those with the disease, while specificity is the proportion of correct negative results among those without the disease. The script uses a two-by-two table to illustrate these concepts and provides a formula for calculating sensitivity and specificity. It also explains how sensitivity and specificity can be used to rule in or rule out diseases, using the analogy of two dogs with different detection characteristics.
Takeaways
- 📈 Sensitivity is the proportion of true positive results among those who have the disease.
- 📊 Specificity is the proportion of true negative results among those who do not have the disease.
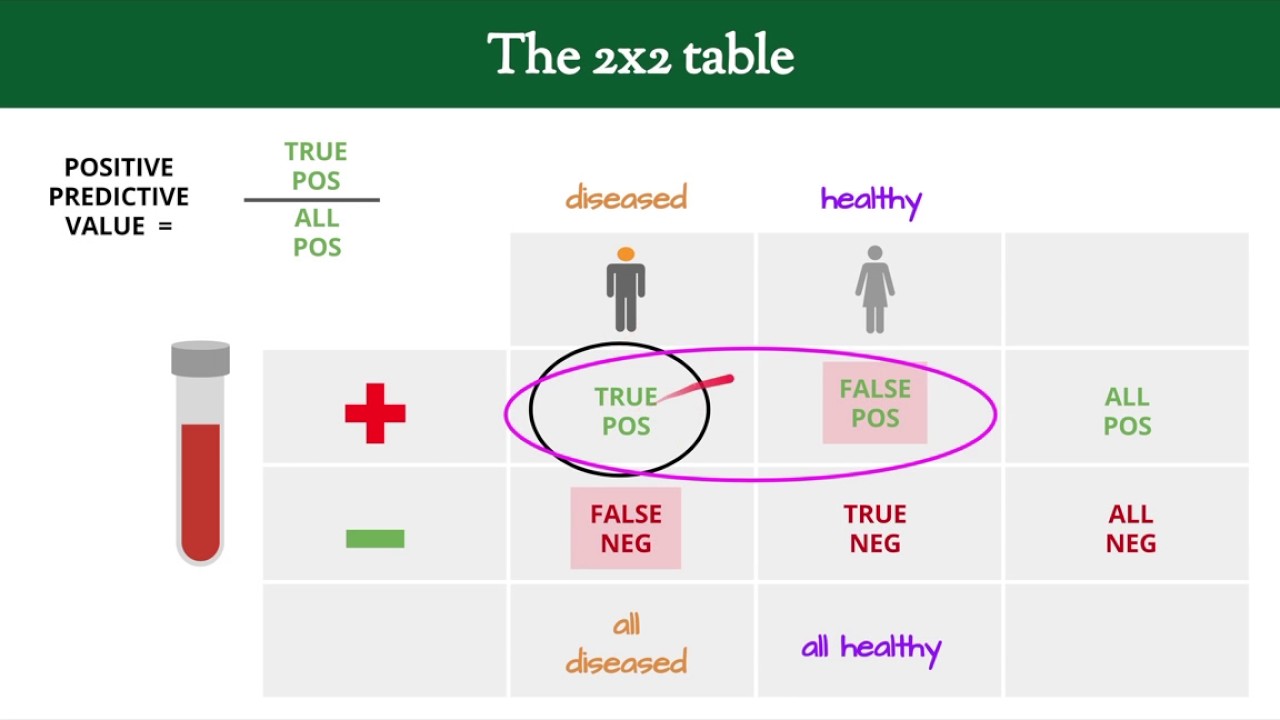
- 🔍 The two-by-two table is a consistent framework for understanding sensitivity and specificity, with disease status across the top and test results down the side.
- 💡 Sensitivity is calculated as True Positive / (True Positive + False Negative), emphasizing the importance of correctly identifying those with the disease.
- 🔎 Specificity is calculated as True Negative / (True Negative + False Positive), focusing on accurately ruling out the disease in those without it.
- 🐶 The example of Max the dog illustrates how a highly sensitive test (or 'Max') can rule out the presence of a disease (or 'criminal') when no positive result is found.
- 🐱 The example of Miley the dog demonstrates how a highly specific test (or 'Miley') can rule in the presence of a disease when a positive result is found.
- 🚫 False negatives are cases where the test fails to detect the disease in those who have it, leading to potentially serious consequences.
- 🚫 False positives occur when the test incorrectly indicates the presence of the disease in those who are disease-free, which can lead to unnecessary follow-up testing.
- 📚 Understanding the concepts of sensitivity and specificity is crucial for evaluating the accuracy and utility of diagnostic tests.
- 🎯 The balance between sensitivity and specificity is key in diagnostic testing, as high sensitivity can rule out disease while high specificity can confirm its presence.
Q & A
What is the definition of sensitivity in the context of diagnostic tests?
-Sensitivity is the proportion of those who have a disease and test positive. It represents the probability that when the disease is present, the test will yield a positive result.
How is specificity defined in relation to diagnostic tests?
-Specificity is the proportion of those who do not have the disease and test negative. It indicates the probability that when the disease is absent, the test will correctly yield a negative result.
What is the two-by-two table used for in evaluating diagnostic tests?
-The two-by-two table is a framework used to organize the results of diagnostic tests into four categories: true positives, false positives, true negatives, and false negatives. It helps in understanding and calculating sensitivity and specificity.
What are the components of the sensitivity formula?
-The sensitivity formula is calculated as True Positive / (True Positive + False Negative). It measures the performance of a test in correctly identifying those with the disease.
How does the specificity formula differ from the sensitivity formula?
-The specificity formula is calculated as True Negative / (True Negative + False Positive). It measures the test's ability to correctly identify those without the disease, which is the opposite of what sensitivity measures.
What are the implications of a high sensitivity in a diagnostic test?
-A high sensitivity means the test is very good at ruling out the absence of a disease. If the test is highly sensitive and yields a negative result, it is likely that the person does not have the disease.
What does a high specificity value indicate about a diagnostic test?
-A high specificity value indicates that the test is good at correctly identifying those without the disease, meaning it has a low rate of false positives. If the test is highly specific and yields a positive result, it is likely that the person has the disease.
What are the consequences of false negatives and false positives in diagnostic testing?
-False negatives can lead to a failure to detect a disease when it is present, potentially leading to delayed treatment. False positives can result in unnecessary treatment or anxiety for individuals who do not actually have the disease.
How can the example of the two dogs, Max and Miley, help understand sensitivity and specificity?
-Max, the sensitive dog, represents a test with high sensitivity; he barks at everything, ensuring no potential threat is missed. However, this can lead to false positives. Miley, the specific dog, represents a test with high specificity; she only barks at the specific threat (criminals in red), reducing false positives but potentially missing other threats (criminals in blue).
What is the mnemonic for remembering the formula for sensitivity?
-The mnemonic is to focus on the 'n' in 'SN' (sensitivity), which stands for 'true positive over true positive plus false negative'. This helps remember the order of the terms in the sensitivity formula.
How does the concept of ruling in and ruling out diseases relate to sensitivity and specificity?
-Sensitivity is related to ruling out diseases; if a highly sensitive test is negative, you can be confident that the disease is not present. Specificity is related to ruling in diseases; if a highly specific test is positive, you can be confident that the disease is present.
Outlines
🧪 Introduction to Evaluating Diagnostic Tests: Sensitivity and Specificity
This paragraph introduces the topic of evaluating diagnostic tests, focusing on sensitivity and specificity. It explains that sensitivity is the proportion of true positive results among those who have the disease, and it emphasizes the importance of a consistent framework for understanding these concepts. The framework is illustrated using a two-by-two table to differentiate between true positives, false negatives, true negatives, and false positives. The formula for sensitivity is provided, and the concept is further clarified with a mnemonic to aid in memorization. The paragraph also contrasts sensitivity with specificity, highlighting their roles in ruling in or ruling out diseases.
🐶 Using Canine Sensitivity and Specificity to Explain Disease Diagnosis
The second paragraph uses a metaphor involving two dogs, Max and Miley, to illustrate how sensitivity and specificity function in disease diagnosis. Max, a sensitive dog, is used to explain how a high sensitivity can rule out the absence of a disease (in this case, an intruder), as he will alert to almost anything (true positives and false positives). However, when he doesn't bark (a negative result), it can be confidently assumed that there is no intruder outside. Miley, on the other hand, represents specificity; she only barks at criminals wearing red (true positives), ignoring other stimuli (true negatives). If Miley barks, it can be concluded that a criminal wearing red is present (a positive result), demonstrating how specificity can rule in the presence of a disease. The paragraph concludes by encouraging viewers to tune in for the next video on biostatistics and to like and subscribe for more content.
Mindmap
Keywords
💡Sensitivity
💡Specificity
💡True Positive
💡False Negative
💡True Negative
💡False Positive
💡Two-by-Two Table
💡Diagnostic Test
💡Probability
💡Mnemonic
💡Ruling In and Ruling Out
Highlights
The introduction of a new series on biostats focusing on evaluating diagnostic tests.
Explanation of sensitivity in the context of diagnostic tests, defined as the proportion of those with the disease who test positive.
The importance of a consistent framework for understanding sensitivity, using a two-by-two table to organize information.
Definition of true positives, true negatives, false negatives, and false positives in the context of diagnostic testing.
The formula for calculating sensitivity, which is true positives divided by the sum of true positives and false negatives.
A mnemonic for remembering the formula for sensitivity, focusing on the 'n' in 'SN' to represent the division of true positives by the sum of true and false negatives.
Contrasting sensitivity with specificity, defined as the proportion of those without the disease who test negative.
The formula for specificity, which is true negatives divided by the sum of true negatives and false positives.
A visual mnemonic for specificity, remembering false positives and flipping the other terms to 'negative'.
The role of sensitivity in ruling out diseases, using the example of a sensitive dog named Max that barks at everything, including false positives.
The interpretation of Max's barking (sensitivity) in ensuring that if he does not bark, there is no one outside, thus ruling out the presence of a threat.
The role of specificity in ruling in diseases, using the example of Miley, a dog that only barks at criminals wearing red.
The interpretation of Miley's barking (specificity) in confirming the presence of a threat when she barks, thus ruling in the presence of a criminal wearing red.
The explanation of how sensitivity and specificity work together to rule out or rule in diseases, using the analogy of two dogs with different alerting behaviors.
The invitation to tune in for the next video in the biostats series, encouraging viewers to like and subscribe.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: