How to calculate Sensitivity and Specificity
TLDRThis informative video from Physiotutors explains how to calculate sensitivity and specificity, key metrics in clinical diagnostics. It introduces the concept using a 2x2 truth table and defines true positives (TP), false positives (FP), false negatives (FN), and true negatives (TN). The video then demonstrates how to derive sensitivity (proportion of true positives among those with the disease) and specificity (proportion of true negatives among those without the disease) using a step-by-step example with given numbers. It highlights the importance of these values in understanding test accuracy but also points out their limitations, suggesting viewers learn about positive and negative predictive values in a follow-up video for a more comprehensive understanding.
Takeaways
- 📈 Sensitivity is the proportion of patients with a positive test result among all patients with the disease.
- 📊 Specificity is the proportion of patients with a negative test result among all patients without the disease.
- 🤒 True Positive (TP) is when the test correctly identifies a patient with the disease.
- 🚫 False Positive (FP) occurs when the test incorrectly indicates a patient has the disease when they do not.
- 😷 False Negative (FN) is when the test fails to detect the disease in a patient who actually has it.
- 🛡️ True Negative (TN) is when the test correctly identifies a patient as not having the disease.
- 🧠 To calculate sensitivity: (TP / (TP + FN)) * 100 to get a percentage.
- 🧠 To calculate specificity: (TN / (TN + FP)) * 100 to get a percentage.
- 🔍 Sensitivity and specificity are crucial in clinical practice to understand the performance of diagnostic tests.
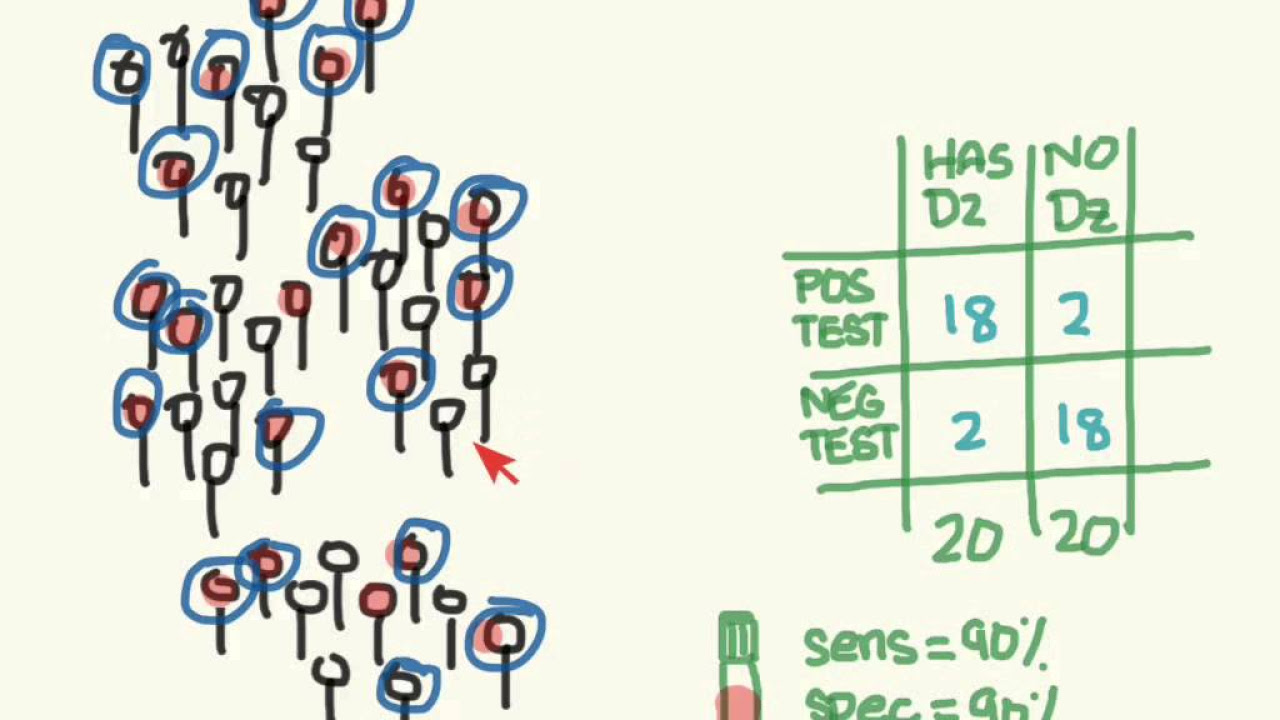
- 📝 Example calculation: Sensitivity = 220 / 250 = 0.88 or 88%; Specificity = 675 / 750 = 0.9 or 90%.
- 🔎 Beyond sensitivity and specificity, positive and negative predictive values are also important for clinical decision-making.
Q & A
What are sensitivity and specificity in clinical practice?
-Sensitivity and specificity are statistical measures used in clinical practice to evaluate the performance of diagnostic tests. Sensitivity is the proportion of true positives among all individuals with the disease, while specificity is the proportion of true negatives among those without the disease.
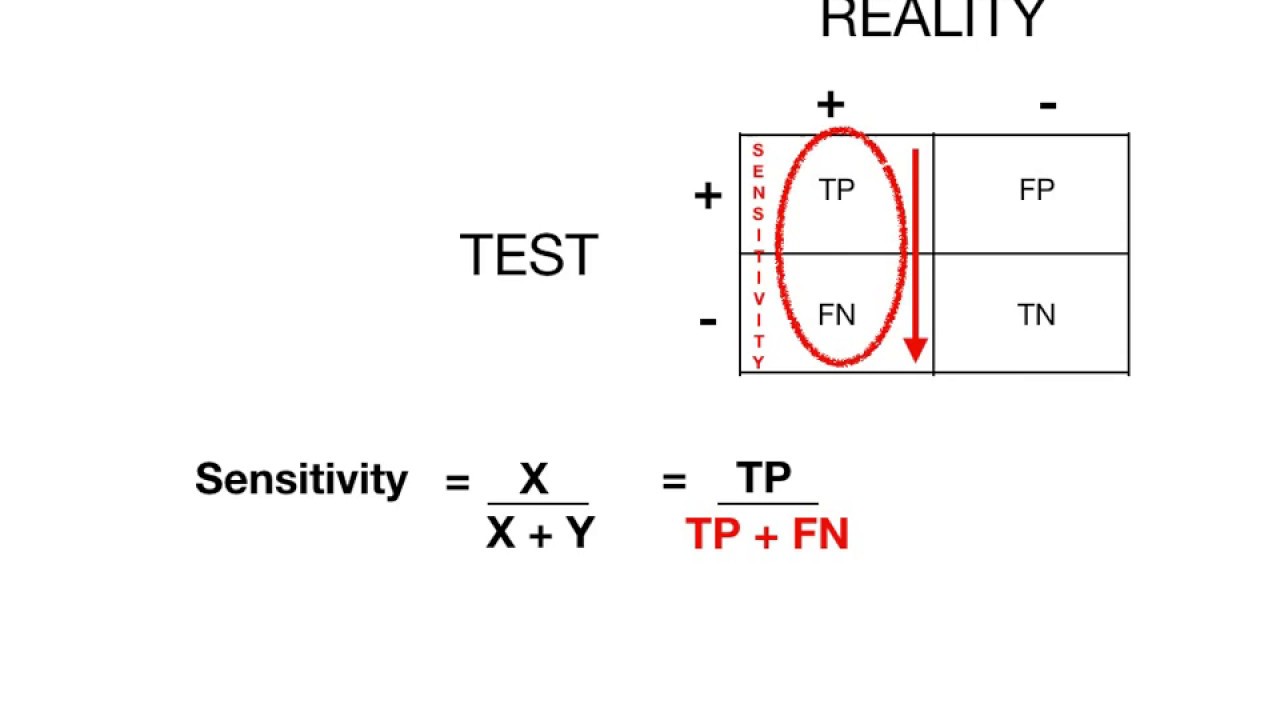
How is a two by two table used in calculating sensitivity and specificity?
-A two by two table, also known as a truth table, is used to organize the outcomes of a diagnostic test into four categories: true positives (TP), false positives (FP), false negatives (FN), and true negatives (TN). This table helps in understanding the relationship between the test results and the actual disease status.
What does a true positive (TP) represent in the context of the two by two table?
-A true positive (TP) represents a situation where the diagnostic test correctly identifies a patient as having the disease when, in fact, they do have it.
How is a false positive (FP) defined?
-A false positive (FP) occurs when the diagnostic test incorrectly identifies a patient as having the disease, even though they do not actually have it.
What is the formula for calculating sensitivity?
-The formula for calculating sensitivity is TP / (TP + FN), where TP is the number of true positives and FN is the number of false negatives.
What does specificity measure in the context of a diagnostic test?
-Specificity measures the proportion of patients without the disease who are correctly identified as such by the diagnostic test. It is calculated as TN / (TN + FP), where TN is the number of true negatives and FP is the number of false positives.
Why is it important to know the sensitivity and specificity of a diagnostic test?
-Knowing the sensitivity and specificity of a diagnostic test is important because it helps healthcare providers understand the test's accuracy and reliability. High sensitivity means the test is good at identifying those with the disease, while high specificity means the test is good at ruling out the disease in those who do not have it.
What are the limitations of sensitivity and specificity in clinical practice?
-The limitations of sensitivity and specificity in clinical practice include the fact that they require knowledge of the disease status of the individuals being tested, which is often not available in real-world settings. Additionally, they do not provide information on the likelihood of the disease given a positive or negative test result, which is where positive and negative predictive values come into play.
How can you calculate the positive predictive value (PPV) and negative predictive value (NPV)?
-Positive predictive value (PPV) is calculated as TP / (TP + FP), and it estimates the probability that a person with a positive test result actually has the disease. Negative predictive value (NPV) is calculated as TN / (TN + FN), and it estimates the probability that a person with a negative test result does not have the disease.
What is an example calculation for sensitivity in the script?
-In the example given, sensitivity is calculated as 220 (TP) divided by the sum of 220 (TP) and 30 (FN), which equals 220 / 250, resulting in a sensitivity of 88%.
What is an example calculation for specificity in the script?
-In the example, specificity is calculated as 675 (TN) divided by the sum of 675 (TN) and 75 (FP), which equals 675 / 750, resulting in a specificity of 90%.
How can you enhance your understanding of sensitivity and specificity?
-To enhance your understanding of sensitivity and specificity, watch the video mentioned in the script that provides further explanation and examples of how to calculate positive and negative predictive values, which complement sensitivity and specificity in clinical decision-making.
Outlines
📊 Understanding Sensitivity and Specificity
This paragraph introduces the concepts of sensitivity and specificity, explaining their importance in clinical practice. It outlines the process of calculating these metrics using a two-by-two table that categorizes test results and disease status. The definitions of sensitivity (the proportion of true positives among those with the disease) and specificity (the proportion of true negatives among those without the disease) are provided, along with a formula for their calculation. An example is given to illustrate how to apply these formulas in practice, resulting in a sensitivity of 88% and a specificity of 90%.
🤔 Limitations of Sensitivity and Specificity
The second paragraph discusses the limitations of sensitivity and specificity, noting that they require prior knowledge of disease prevalence. It highlights the need for positive and negative predictive values in practical scenarios where this information is unknown. The video script encourages viewers to watch an accompanying video to learn more about these predictive values. The video concludes with a call to action for viewers to engage with the content, ask questions, and follow Physiotutors on various platforms.
Mindmap
Keywords
💡Sensitivity
💡Specificity
💡True Positive (TP)
💡False Positive (FP)
💡False Negative (FN)
💡True Negative (TN)
💡Two by Two Table
💡Positive Predictive Value
💡Negative Predictive Value
💡Clinical Practice
💡Diagnostic Test
Highlights
The video explains how to calculate sensitivity and specificity.
Sensitivity and specificity are important in clinical practice.
A two by two table, or truth table, is used to define and calculate sensitivity and specificity.
True positive (TP) is when the test says positive and the patient has the disease.
False positive (FP) occurs when the test is positive but the patient does not have the disease.
False negative (FM) is when the test is negative but the patient actually has the disease.
True negative (TN) is when both the test and the patient's condition are negative.
Sensitivity is the proportion of patients with a positive test among all patients with the disease.
Specificity is the proportion of patients with a negative test among those without the disease.
An example is provided to illustrate the calculation of sensitivity and specificity.
Sensitivity is calculated by dividing true positives by the sum of true positives and false negatives.
Specificity is calculated by dividing true negatives by the sum of true negatives and false positives.
In practice, positive and negative predictive values are used instead of sensitivity and specificity.
The video encourages viewers to watch the next video for more information on predictive values.
The video concludes with a call to action for viewers to engage and follow Physiotutors on social media.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: