3 Paradoxes That Gave Us Calculus
TLDRThis video delves into the origins of calculus, exploring three paradoxes by Zeno of Elea that challenge our understanding of motion, space, and time. It explains how these paradoxes led to the development of key calculus concepts such as limits, integration, and derivatives. The video also touches on the philosophical debate about whether math is a human invention or a natural discovery, highlighting the impact of calculus on our comprehension of the world.
Takeaways
- 📚 Calculus is the mathematics of change, essential for various fields like engineering, biology, and chemistry.
- 🌐 The word 'calculus' originates from Latin, meaning 'small stones', symbolizing the breaking down of large problems into smaller parts.
- 🧐 Zeno of Elea's paradoxes challenged the notion of motion, suggesting that an infinite number of steps are required to complete a journey, which seems impossible.
- 🔢 The concept of limits in calculus addresses the problem of infinite series, showing that although there are infinitely many terms, the sum can approach a finite value.
- 📈 The idea of limits is used to understand what happens just before reaching infinity, without actually reaching it.
- 🏢 Bonaventura Cavalieri's work on calculating the area of shapes led to the development of integration in calculus.
- 📊 Integration involves breaking shapes into smaller parts (like rectangles under a curve) and summing their areas to approximate the total area.
- 🔎 The paradox of the arrow (or bullet) questions the concept of motion, as an object frozen in time does not move, yet it appears to when observed over a period.
- 🚀 Calculus, though seemingly man-made, is a tool that helps us describe and understand natural phenomena, blurring the line between invention and discovery.
- 🎥 The video script mentions a documentary by Hannah Fry exploring the question of whether math is an invention or a discovery, available on the streaming platform Nebula.
Q & A
What is the significance of the word 'calculus' in the context of mathematics?
-Calculus is the mathematics of change, dealing with problems where a larger entity is broken down into smaller parts. It's essential for various fields, including engineering, biology, and chemistry, for tasks such as determining material needs, disease spread rates, and measuring chemical reactions.
How did Zeno of Elea's paradoxes contribute to the development of calculus?
-Zeno's paradoxes, such as the one involving an infinite number of halfway points, challenged traditional logic and understanding of motion and space. These paradoxes led to the invention of key calculus concepts like limits, which help resolve problems involving infinite series and approaching values without actually reaching them.
What is the concept of 'limits' in calculus, and how does it address Zeno's paradoxes?
-The concept of limits in calculus allows us to understand the behavior of a function as it approaches a particular value without necessarily reaching it. It addresses Zeno's paradoxes by providing a framework to analyze infinite series and their sums, showing that even with an infinite number of terms, certain sums can converge to a finite value.
How did Bonaventura Cavalieri's work on shapes lead to the development of integration?
-Bonaventura Cavalieri's attempt to find the area of irregular shapes using known formulas for regular shapes led to the concept of integration. He imagined shapes as composed of width-less lines, which later evolved into the idea of breaking shapes into infinitesimally thin rectangles to approximate areas under curves, leading to the mathematically rigorous method of integration.
What is the process of integration in calculus, and how does it relate to the concept of limits?
-Integration in calculus is the process of combining many small elements to calculate the area under a curve or the volume of a solid. It involves breaking a shape into infinitesimally thin slices and summing their areas or volumes. This process is closely related to the concept of limits, as it involves letting the width of these slices approach zero to find an accurate area or volume.
How does Zeno's arrow paradox challenge our understanding of motion and time?
-Zeno's arrow paradox questions the existence of motion by arguing that an arrow in flight, when frozen at any given moment, is not moving. This paradox suggests that a collection of motionless moments cannot constitute motion, challenging our intuitive understanding of how change occurs over time and leading to deeper explorations in calculus regarding instantaneous speed and rate of change.
What is the concept of 'instantaneous speed' in calculus, and how is it calculated?
-Instantaneous speed is the speed of an object at a specific moment in time. In calculus, it is calculated using the concept of derivatives, which involve taking the limit of the average speed as the time interval approaches zero. This gives the slope of the tangent line to the curve at a particular point, representing the exact speed at that instant.
How do paradoxes contribute to the advancement of mathematical thought?
-Paradoxes challenge existing beliefs and intuitions, forcing mathematicians to reevaluate and refine their understanding. They can lead to the discovery of new mathematical concepts, the refinement of existing theories, and a deeper exploration of mathematical ideas, as seen with the development of calculus through addressing Zeno's paradoxes.
What is the philosophical debate surrounding calculus mentioned in the script?
-The philosophical debate mentioned in the script concerns whether calculus is an invention or a discovery. The speaker initially believed that math is a discovery, with patterns found in nature. However, calculus, being a complex and abstract system, seems more like a human invention, existing only in our minds and not directly observable in the natural world.
What are the key concepts in calculus that emerged from the paradoxes discussed in the script?
-The key concepts in calculus that emerged from the discussed paradoxes are limits, integration, and derivatives. Limits help us understand the behavior of functions at infinity, integration allows us to calculate areas and volumes by summing infinitesimally small elements, and derivatives provide a way to determine instantaneous speed and rate of change.
How does the script relate the historical development of calculus to modern educational content?
-The script connects the historical development of calculus to modern educational content by mentioning the work of educational YouTube creators and streaming platforms like CuriosityStream and Nebula. It highlights the ongoing exploration of mathematical ideas through documentaries and feature videos, encouraging viewers to engage with these resources to deepen their understanding of calculus and mathematical concepts.
Outlines
📚 The Birth of Calculus: Zeno's Paradoxes and Infinite Series
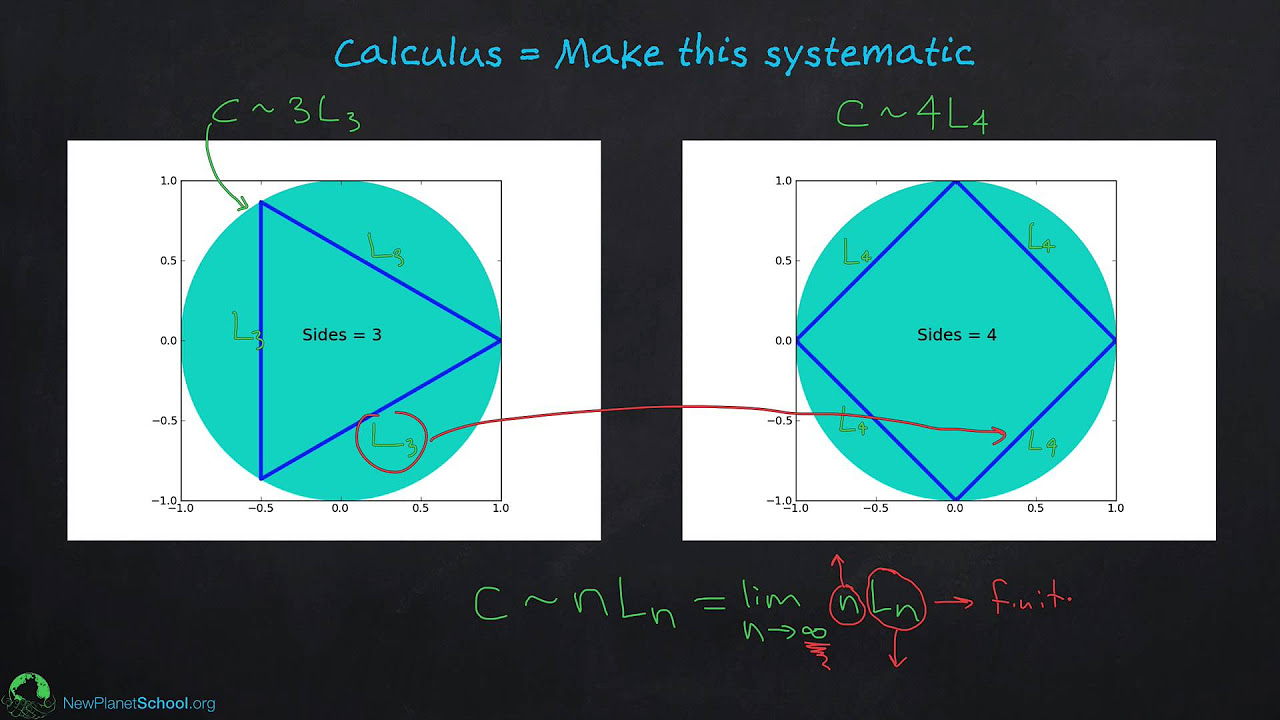
This paragraph introduces the concept of calculus as the mathematics of change, highlighting its importance in various fields such as engineering, biology, and chemistry. It delves into the origins of calculus, which were shaped by paradoxes, particularly those proposed by Zeno of Elea. The paradox of the infinite number of half points in a journey is discussed, illustrating the logical conundrum of motion and the concept of infinity. The paragraph explains how the mathematical tool of limits was developed to address such paradoxes, allowing for the understanding of infinite series and their summation without actually reaching infinity. The concept of limits is shown to be fundamental to calculus, dealing with the behavior of quantities as they approach certain values.
📐 The Paradox of Shapes and the Birth of Integration
The second paragraph explores the historical challenge of finding the area of irregular shapes, leading to the introduction of Bonaventura Cavalieri's theory of indivisibles. This theory attempted to calculate areas by using known formulas for regular shapes and adjusting them for new shapes. However, it faced issues, such as the paradox of zero-width lines contributing to an area. The paragraph explains how modern calculus resolved this with the concept of integration, which involves breaking shapes into infinitesimally thin rectangles to approximate areas more accurately. The technique of letting the width of these rectangles approach zero, while the number of rectangles approaches infinity, is described, emphasizing the role of limits in this process.
🏹 Zeno's Arrow and the Concept of Instantaneous Speed
The third paragraph discusses Zeno's arrow paradox, which questions the nature of motion over time. It challenges the notion of an object's movement at a specific instant by arguing that a frozen moment in time shows no movement. The paradox raises the question of how a series of motionless moments can create the illusion of continuous motion. The paragraph connects this to the previous discussions on space and area, suggesting that similar logic can be applied to understand motion. It introduces the concept of instantaneous speed, which is calculated using derivatives and limits. The process of finding the speed at a specific time involves taking the limit as the time interval approaches zero, resulting in the slope of the tangent line to the curve at that point, providing a precise measure of speed at any given moment.
Mindmap
Keywords
💡Calculus
💡Zeno of Elea
💡Paradox
💡Limit
💡Integration
💡Derivative
💡Infinity
💡Instantaneous Speed
💡Nebula
💡CuriosityStream
Highlights
Calculus is the mathematics of change, derived from Latin 'calculus' meaning small stones, symbolizing the breaking down of large problems into smaller, manageable parts.
The importance of calculus in various fields such as engineering, biology, and chemistry, where it is used for determining material needs, disease spread rates, and measuring chemical reactions.
The origin of calculus is rooted in paradoxes, particularly those proposed by Zeno of Elea, which challenged the understanding of motion and infinity.
Zeno's paradox of motion, which argues that reaching a destination requires passing through an infinite number of halfway points, thus making motion impossible.
The concept of the mathematical limit, which is a fundamental tool in calculus, was developed to address the issues raised by Zeno's paradoxes.
The sum of an infinite series of fractions in Zeno's paradox approaches the value of one, illustrating the concept of a limit in calculus.
The historical attempt by Bonaventura Cavalieri to find the area of shapes using known formulas, leading to the development of integration in calculus.
The paradox of using width-less lines to find the area of a shape, which led to the modern concept of integration in calculus.
Integration in calculus involves breaking shapes into smaller pieces and combining them to find the whole area, approaching the concept of width-less lines.
Zeno's arrow paradox, which questions the existence of motion by examining the concept of time and the illusion of movement.
The use of limits to calculate instantaneous speed, demonstrating the concept of derivatives in calculus.
The philosophical debate on whether calculus is a man-made invention or a discovery of natural mathematical patterns.
The promotion of Nebula, a streaming platform for educational content, and its connection to the exploration of mathematical concepts like those in calculus.
The mention of a documentary by Hannah Fry on CuriosityStream, which explores the question of whether math is an invention or a discovery, providing a visual and historical perspective on the subject.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: