Solving Exact Differential Equations (Differential Equations 29)
TLDRIn this instructional video, the presenter guides viewers through the process of solving exact differential equations by identifying potential functions. The video emphasizes the importance of verifying the equation's exactness through mixed partials and provides a step-by-step approach to finding the potential function using integration and partial derivatives. The presenter offers multiple examples of varying difficulty, aiming to build confidence and ensure understanding of the concepts involved.
Takeaways
- 📚 The video focuses on practicing solving exact differential equations and finding potential functions from them.
- 🧐 To determine if an equation is exact, one must check if the mixed partial derivatives with respect to X and Y are equal.
- 🤔 The process involves integrating the function M with respect to X and then taking the derivative with respect to Y to find the missing function of Y.
- 🔄 It's crucial to remember that when integrating with respect to one variable, the other variable's terms are treated as constants.
- 📈 The choice of whether to integrate M with respect to X or N with respect to Y first depends on which makes the calculation easier.
- 🌟 If the mixed partials are not equal, the equation is not an exact differential equation of some potential function.
- 🛠️ The video provides several examples to illustrate the process of solving exact differential equations and emphasizes the importance of practice.
- 🧮 When solving, it's necessary to account for the constant term that arises from the partial derivative with respect to the variable not integrated.
- 🔗 The video also discusses the concept of level curves and how potential functions are related to them.
- 📌 The process of solving exact differential equations involves a combination of integration and differentiation to find the potential function.
- 🎯 The video encourages viewers to apply the techniques on their own to build confidence and understanding of the material.
Q & A
What is the primary focus of the video?
-The primary focus of the video is to practice solving exact differential equations and finding potential functions from them.
Why is it important to check if a given equation is an exact differential equation?
-It is important because only if the mixed partials of the equation are equal can we guarantee that it is an exact differential equation of some potential function, which allows us to proceed with solving it.
How can you determine if a differential equation is exact based on the script?
-You can determine if a differential equation is exact by checking if the mixed partial derivatives with respect to X and Y are equal. If they are, the equation is exact and can be associated with a potential function.
What is the significance of the potential function in the context of exact differential equations?
-The potential function is significant because it represents the function from which the exact differential equation originates. If an exact differential equation can be associated with a potential function, it means the equation is a total differential of that function.
How does the process of solving an exact differential equation begin?
-The process begins by checking if the given differential equation is exact by comparing the mixed partial derivatives. Once confirmed, the next step is to integrate with respect to the variable and then take a derivative with respect to the other variable to find the potential function.
What is the role of initial values in solving exact differential equations?
-Initial values are used to solve for the arbitrary constant that arises when integrating to find the potential function. By plugging in the initial conditions, you can determine the specific value of the constant and arrive at a particular solution.
Why is it necessary to consider the domain of the potential function?
-The domain of the potential function is necessary to consider because certain functions may not be defined or continuous for all values within their domain. Understanding the domain ensures that the solutions are valid and applicable within the given context.
What happens if the mixed partial derivatives are not equal?
-If the mixed partial derivatives are not equal, the equation is not an exact differential equation of some potential function, and additional methods, such as the integrating factor, may be required to solve it.
How does the process of integrating and taking derivatives help in finding the potential function?
-The process of integrating and taking derivatives is a way to reverse the operation of differentiation. By integrating with respect to one variable, you undo the derivative with respect to the other, allowing you to reconstruct the potential function from its differential equation.
What is the role of the arbitrary constant (C) in the potential function?
-The arbitrary constant (C) represents the unknown additive constant that is inherent in the integration process. It accounts for the fact that the integral of a derivative can result in multiple functions that differ by a constant, all of which are valid potential functions for the given differential equation.
Outlines
📚 Introduction to Solving Exact Differential Equations
The video begins with an introduction to solving exact differential equations, emphasizing the importance of understanding why and how they work. The speaker plans to provide numerous examples to practice solving these equations and working with initial values. The focus is on the technique of solving exact differential equations, ensuring that the viewer feels confident and well-prepared.
🧐 Understanding the Nature of Exact Differential Equations
The speaker explains the concept of exact differential equations by discussing the conditions under which an equation can be considered exact. The key condition is that the mixed partial derivatives must be equal, which is a result of the potential function being continuous and differentiable over a certain region. The speaker also introduces the notation for partial derivatives and sets the groundwork for checking the exactness of a given equation.
🔍 Examining the Process of Identifying Potential Functions
The video delves into the process of identifying potential functions from exact differential equations. The speaker demonstrates how to work backwards from the differential equation to find the potential function, emphasizing the importance of equal mixed partials. The process involves taking the integral of the partial derivative with respect to one variable and then taking the partial derivative with respect to the other variable to find the missing function.
📝 Working Through an Example: Solving for Potential Function
The speaker works through a detailed example of solving for a potential function from an exact differential equation. The process involves integrating the partial derivative with respect to one variable, taking the partial derivative with respect to the other variable, and setting them equal to each other to solve for the unknown function. The example illustrates the steps and considerations involved in solving such equations.
🤔 Reflecting on the Integration and Derivative Process
The speaker reflects on the process of integration and differentiation used to solve exact differential equations. They emphasize the importance of choosing the easier variable to integrate with respect to and the need to understand the implications of integrating with respect to one variable over the other. The speaker also discusses the concept of arbitrary constants and how they relate to the level curves of potential functions.
📈 Demonstrating the Integration of a Challenging Equation
The speaker tackles a complex example, demonstrating the process of integrating a challenging exact differential equation. They explain the steps of finding the partial derivative with respect to the chosen variable, integrating to find the potential function, and then taking the derivative with respect to the other variable to find the missing function. The example serves to reinforce the techniques and considerations discussed earlier in the video.
🔧 Applying the Method to Another Complicated Equation
The speaker applies the method for solving exact differential equations to another complicated example. They walk through the process of identifying the partial derivatives, integrating with respect to the chosen variable, and solving for the missing function. The example highlights the importance of understanding the underlying principles and being able to adapt the method to different scenarios.
🎓 Finalizing the Solution and Discussing Initial Values
The speaker finalizes the solution to the previous example by solving for the constant using an initial value. They emphasize the importance of solving for the constant before attempting to solve for the variables, as it simplifies the process. The speaker also discusses the significance of initial values in providing a particular solution to the differential equation.
🚀 Wrapping Up and Encouraging Further Practice
In the concluding part of the video, the speaker wraps up the discussion on solving exact differential equations. They encourage the viewer to practice the techniques learned and to understand the nuances involved. The speaker also teases the next video, which will cover the use of an integrating factor to solve equations that are not exact.
Mindmap
Keywords
💡Exact Differential Equation
💡Potential Function
💡Mixed Partial Derivatives
💡Integration
💡Partial Derivative
💡Total Differential
💡Arbitrary Constant
💡Level Curves
💡Integration Techniques
💡Product Rule
Highlights
The video focuses on practicing solving exact differential equations and finding potential functions from them.
The importance of understanding the concept of exact differential equations is emphasized for confident problem-solving.
A potential function f of X and Y can be found if the mixed partials are equal, indicating continuity and differentiability in a region.
The process of checking mixed partials as the first step in solving an exact differential equation is discussed.
The technique of integrating M with respect to X and differentiating with respect to Y to find the potential function is explained.
The video demonstrates that the order of integration (M with respect to X or N with respect to Y) does not matter in solving the equation.
The concept of partial derivatives and how they relate to exact differential equations is clarified.
An example is provided to illustrate the process of finding a potential function from an exact differential equation.
The importance of recognizing when a function is missing X terms and treating it as a constant is highlighted.
The process of solving for the missing function of Y by integrating and differentiating is detailed.
The significance of the level curves of potential functions and how they relate to exact differential equations is discussed.
The video emphasizes the importance of checking mixed partials before proceeding with solving an exact differential equation.
A comprehensive example is provided to demonstrate the entire process of solving an exact differential equation, including finding the potential function and handling initial values.
The concept of integrating and differentiating with respect to the opposite variable to solve for the missing function is explained.
The video concludes with a reminder of the importance of understanding the nuances of solving exact differential equations and the necessity of checking mixed partials.
Transcripts
Browse More Related Video

What are Exact Differential Equations (Differential Equations 28)

Introduction to Partial Derivatives (Calculus 3)

Integrating Factor for Exact Differential Equations (Differential Equations 30)
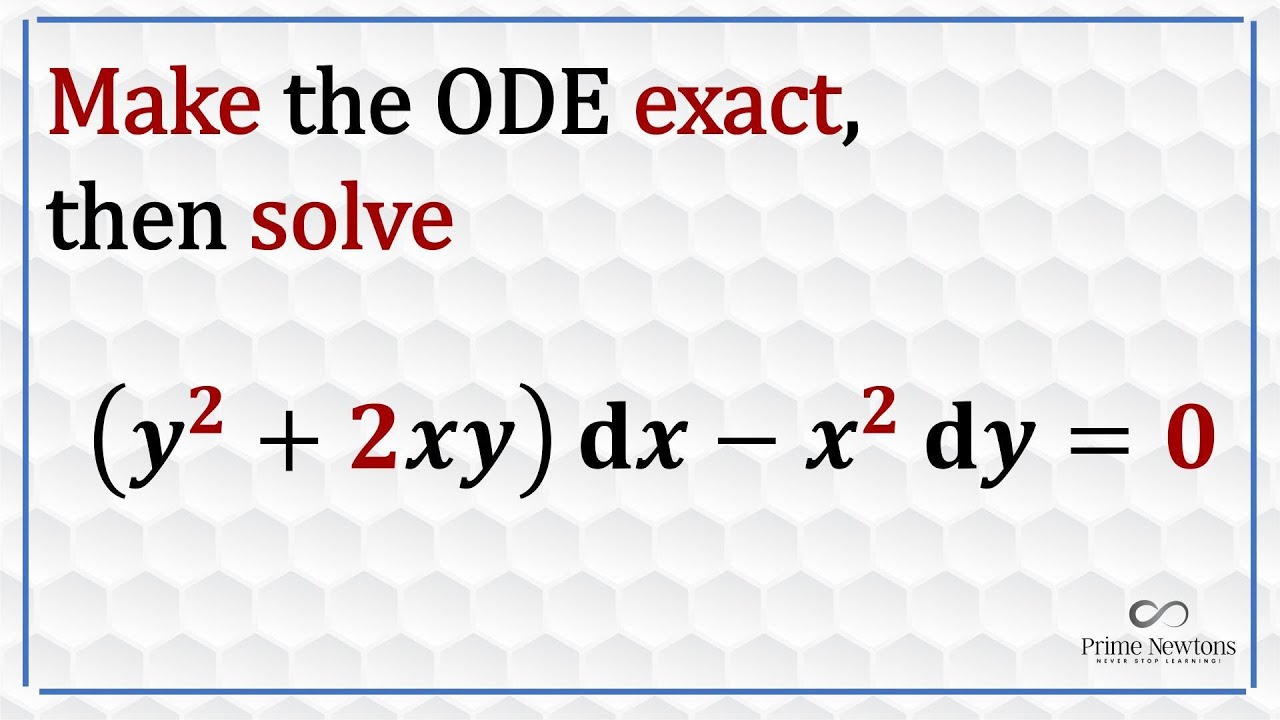
How to solve exact and non-exact ODE

Conservative Vector Fields & Potential Functions
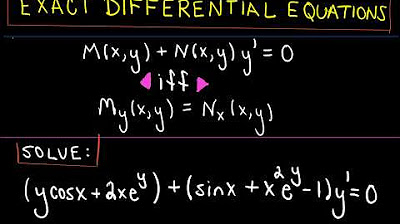
Exact Differential Equations
5.0 / 5 (0 votes)
Thanks for rating: