8.03 - Lect 1 - Periodic Phenomena, SHO, Complex Notation, Physical Pendulum
TLDRIn this lecture, Professor Walter Lewin explores the fascinating world of waves, vibrations, and oscillations, drawing connections between everyday phenomena and complex physics concepts. From the heartbeat to the swinging of a pendulum, Lewin uses engaging demonstrations and real-world examples to illustrate the principles of simple harmonic motion, the impact of mass and amplitude on oscillations, and the mathematical beauty of Euler's formula. He challenges students with thought-provoking questions and mini-quizzes, emphasizing the importance of understanding the underlying physics rather than just memorizing equations.
Takeaways
- 📚 The course focuses on waves, vibrations, and oscillations, including both periodic and non-periodic events.
- 💡 Everyday actions like heartbeats, breathing, and daily routines are examples of periodic oscillations.
- 🚀 Walter Lewin introduces the concept of simple harmonic oscillations and their mathematical representation.
- 📐 The period of oscillation for a simple pendulum is independent of its mass and depends on the length of the pendulum and gravitational acceleration.
- 🔄 Euler's disk demonstrates the fascinating interplay between azimuthal and wobbling motions, with the wobbling frequency increasing as the azimuthal motion slows down.
- 🎵 Sound waves are a form of oscillations, and the human hearing range is from 20 Hz to 20 kHz, with some animals capable of hearing beyond this range.
- 📊 Lewin conducts a hearing test with the class, showing that the highest frequency one can hear decreases with age.
- 🌀 The motion of objects like electrons, atoms, and molecules, as well as celestial bodies, are examples of periodic and oscillatory motion.
- 🔧 The spring system is used to illustrate simple harmonic motion, with the period of oscillation depending on the spring constant and mass.
- 🤔 A thought experiment with a pipe heated and cooled to generate oscillations prompts students to think about the underlying physics.
- 📐 The physical pendulum's period of oscillation is derived, highlighting the importance of calculating the moment of inertia about the point of rotation.
Q & A
What is the main topic of the course that Walter Lewin is teaching?
-The main topic of the course is waves and vibrations, focusing on oscillations and periodic or not so periodic events.
How does Walter Lewin demonstrate periodic motion in the classroom?
-Walter Lewin demonstrates periodic motion by drinking orange juice, showing how the liquid moves in a periodic manner rather than a steady stream.
What is the significance of Euler's disk in the course?
-Euler's disk is used to illustrate the concept of wobbling and its relationship with the azimuthal motion, where the frequency of wobble increases while the azimuthal motion slows down.
How does Walter Lewin test the hearing range of his students?
-Walter Lewin tests his students' hearing range by generating sounds at different frequencies and asking them to raise their hands when they can no longer hear the sound.
What is the formula for simple harmonic oscillation?
-The formula for simple harmonic oscillation is x = x0 * cos(ωT + Φ), where x0 is the amplitude, ω is the angular frequency, T is the time, and Φ is the phase angle.
How does the period of oscillation for a spring-mass system relate to the mass and spring constant?
-The period of oscillation for a spring-mass system is given by T = 2π * √(M/K), where M is the mass and K is the spring constant.
What is the role of the moment of inertia in the oscillation of a physical pendulum?
-The moment of inertia plays a crucial role in determining the period of oscillation of a physical pendulum. It is used in the formula T = 2π * √(I/(BMG)), where I is the moment of inertia about point P, B is the distance from point P to the center of mass, M is the mass, and G is the acceleration due to gravity.
How does Walter Lewin demonstrate the independence of the pendulum period from the mass of the object?
-Walter Lewin demonstrates this by swinging the pendulum with different masses attached to it and showing that the period of oscillation remains the same, provided the mass of the string can be ignored.
What is the significance of complex numbers in the study of oscillations?
-Complex numbers are used in the study of oscillations because they simplify the mathematics involved in solving differential equations. They allow for easier manipulation and can be used to represent the amplitude and phase of oscillations in a more convenient form.
How does Walter Lewin engage students with the concept of Euler's formula?
-Walter Lewin engages students by presenting Euler's formula, which relates complex numbers to trigonometric functions, and encourages students to grapple with the concept on their own, offering a challenge to understand its significance and application.
What is the practical application of the concepts taught in the lecture?
-The practical application of the concepts taught in the lecture includes understanding the physics behind everyday phenomena like the swinging of a pendulum, the oscillation of springs, and the propagation of sound waves, as well as solving more complex problems in physics and engineering.
Outlines
🌊 Introduction to Waves and Oscillations
Professor Walter Lewin introduces the course on waves and vibrations, emphasizing the omnipresence of oscillations in daily life, from heartbeats to the motion of liquids. He uses everyday examples to illustrate periodic and non-periodic oscillations and introduces the concept of a toy that challenges the fastest transfer of liquid, hinting at the Euler's disk experiment to be discussed later.
📈 The Physics of Wobbling and Frequency
The discussion shifts to the physics of wobbling, with Lewin explaining how the frequency of wobble increases while the azimuthal motion slows down, as demonstrated by the Euler's disk. He also covers the oscillatory motion of objects like tennis balls and floating objects in liquid, and extends the concept to natural phenomena like wind. The lecture touches on the physics of sound, its relation to oscillation, and the range of human hearing.
🎵 Sound and Hearing: The Tuning Fork Experiment
Lewin conducts a hearing test using a tuning fork to explore the range of human audible frequencies. He explains the concept of Hertz and how the ability to hear high frequencies diminishes with age. The lecture delves into simple harmonic oscillations, their mathematical representation, and the relationship between angular frequency and period.
🔄 Projection of Uniform Circular Motion
The lecture demonstrates the relationship between uniform circular motion and simple harmonic motion through a shadow projection experiment. Lewin explains how the projection of a rotating object onto a line results in simple harmonic motion and how the angular frequency is independent of the amplitude of the motion.
📐 Mass and Spring: The Period of Oscillation
Lewin discusses the period of oscillation for a spring system, emphasizing that it is independent of the amplitude and initial conditions. He conducts an experiment to test the accuracy of the theoretical predictions, adjusting the mass on a spring and measuring the resulting changes in the period of oscillation.
🔢 Measuring the Period of a Spring System
The lecture details the process of measuring the period of a spring's oscillation, highlighting the importance of understanding the accuracy and uncertainty in physical measurements. Lewin uses this experiment to illustrate the principles of simple harmonic motion and the impact of mass on the oscillation period, ultimately confirming the predictions of physics.
🌀 Complex Numbers and Euler's Formula
Lewin introduces complex numbers and Euler's formula, explaining their application in the context of simple harmonic motion. He discusses the complex plane, the representation of complex numbers, and the significance of Euler's formula in simplifying the analysis of oscillatory systems.
🔄 The J to the Power of J Conundrum
The lecture concludes with a deep dive into the complex number J to the power of J, exploring its properties and solutions. Lewin challenges students to solve this non-intuitive problem, emphasizing the value of struggling with complex concepts to achieve a deeper understanding.
🎶 Heat-Induced Oscillation Experiment
Lewin presents a thought-provoking experiment where heat and cooling generate a 110 Hz oscillation in a pipe system. He encourages students to ponder the phenomenon and return to it after a break, also mentioning a mini quiz to be conducted during the break.
⏳ The Pendulum and Its Period
The lecture focuses on the period of oscillation for a pendulum, distinguishing between a simple pendulum and a physical pendulum. Lewin explains the mathematical relationship governing the period and how it is affected by factors such as the length of the pendulum and the mass of the object.
🏋️ Mass Variation and Pendulum Period
Lewin conducts an experiment to demonstrate that the period of a pendulum is independent of the mass of the object, provided the mass of the string can be ignored. He uses himself as a counterweight to show that the period remains the same, reinforcing the principles of pendulum motion.
🔄 Physical Pendulums and Their Dynamics
The lecture delves into the dynamics of physical pendulums, which are more complex than simple pendulums. Lewin explains how to calculate the period of oscillation for a physical pendulum, focusing on the moment of inertia and the torque acting on the system. He presents a method for solving for the period of a hoop pendulum as an example.
📐 Measuring the Radius and Testing the Hoop Pendulum
Lewin describes the process of measuring the radius of a hoop pendulum and uses this measurement to predict the period of oscillation. He then conducts an experiment to test the prediction, comparing the observed period with the theoretical value and confirming the accuracy of the calculations.
Mindmap
Keywords
💡Walter Lewin
💡Periodic Motion
💡Simple Harmonic Oscillation
💡Euler's Disk
💡Complex Numbers
💡Physics Experiments
💡Moment of Inertia
💡Angular Frequency
💡Differential Equations
💡Measurement Uncertainty
Highlights
Walter Lewin introduces the concept of waves and vibrations, emphasizing their ubiquity in everyday life.
Lewin uses a toy to demonstrate the periodic motion of liquid, challenging students to transfer the liquid in 17 seconds during the break.
The Euler's disk is introduced as an example of an object that wobbles in a fascinating way, with the wobbling frequency increasing as the disk slows down.
Lewin explains the difficulty in physics behind the Euler's disk and its unique motion.
The concept of simple harmonic oscillations is introduced, with the equation x = x0 cos(ωt + φ) provided.
Lewin demonstrates the relationship between uniform circular motion and simple harmonic motion through a practical example.
The spring system is used to illustrate simple harmonic motion, with the equation x = A cos(ωt + φ) applied to it.
Lewin conducts a hearing test on students, using sound frequencies to determine the highest frequency they can hear.
The concept of angular frequency and its relation to the period of oscillation is explained, with the equation ω = √(k/m) derived for a spring system.
Lewin emphasizes the importance of understanding the independence of the period of oscillation from the amplitude and initial conditions in simple harmonic motion.
A live demonstration of the period of oscillation for a spring system is conducted, with predictions made based on the mass and spring constant.
The concept of complex numbers and their application in physics, particularly in solving differential equations, is introduced.
Lewin presents a thought-provoking example of an oscillation generated by heat and cooling, challenging students to explain the phenomenon.
The pendulum is discussed as an example of simple harmonic oscillation, with the period given by T = 2π√(L/g), independent of the mass of the object.
Lewin conducts an experiment to demonstrate the independence of the pendulum's period from its mass, using himself as a counterweight.
The concept of the physical pendulum is introduced, with the period depending on the moment of inertia about the point of rotation and the distance to the center of mass.
Lewin calculates the moment of inertia for a hoop pendulum and predicts its period of oscillation, comparing it to a single pendulum with a length of 2r.
An experiment is conducted to test the predicted period of the hoop pendulum, with the results aligning with the theoretical predictions.
Transcripts
Browse More Related Video

8.01x - Lect 11 - Work, Kinetic & Potential Energy, Gravitation, Conservative Forces

For the Love of Physics - Walter Lewin - May 16, 2011
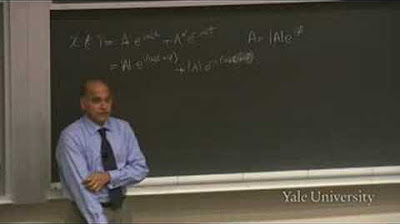
17. Simple Harmonic Motion

16. The Taylor Series and Other Mathematical Concepts

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion

1. Periodic Oscillations, Harmonic Oscillators
5.0 / 5 (0 votes)
Thanks for rating: