16. The Taylor Series and Other Mathematical Concepts
TLDRIn this lecture, Professor Shankar delves into mathematical concepts crucial for understanding physics, starting with the Taylor series, a powerful tool for function approximation. He illustrates its application with examples like e^(x), cos x, and sin x, highlighting its limitations and relevance. The professor then transitions to complex numbers, explaining their properties, operations, and the significance of Euler's formula, e^(iπ) + 1 = 0. The session culminates with an exploration of simple harmonic motion, detailing the physics of oscillations in springs and pendulums, and emphasizing the importance of energy conservation and the role of amplitude and phase in oscillation.
Takeaways
- 📚 The professor begins by transitioning from a previous topic on relativity to introducing mathematical concepts important for physics, emphasizing the importance of problem sets and exams.
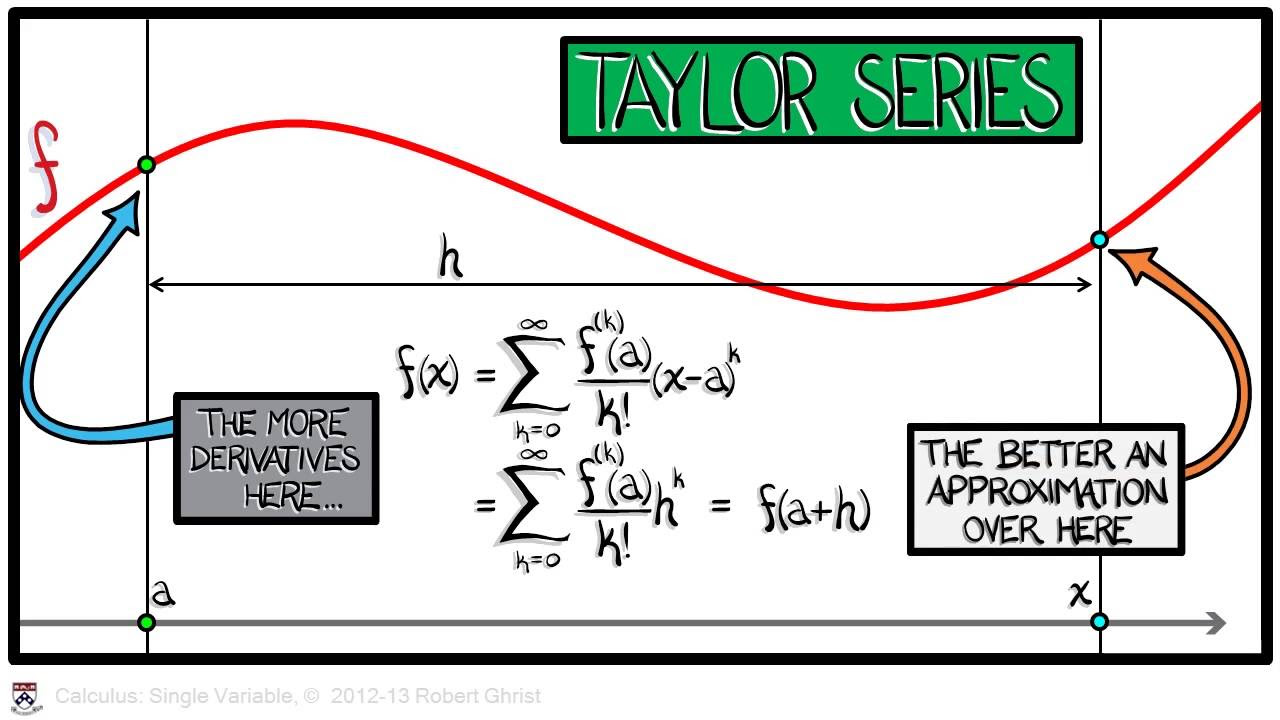
- 🔍 The lecture delves into the concept of Taylor series, a mathematical tool used to approximate functions by polynomials, which is foundational for many applications in physics.
- 📈 The professor explains the Taylor series through the example of approximating the function 1/(1-x) and its limitations, such as not working for |x| > 1, to illustrate the concept of convergence and divergence of series.
- 🎓 The importance of knowing the function's derivatives is highlighted as it allows for constructing a Taylor series approximation that can be as accurate as needed, depending on the number of terms included.
- 🤔 The lecture touches on the philosophical aspect of approximations in physics, stating that while exact answers are often unattainable, good approximations are essential for understanding and describing the world.
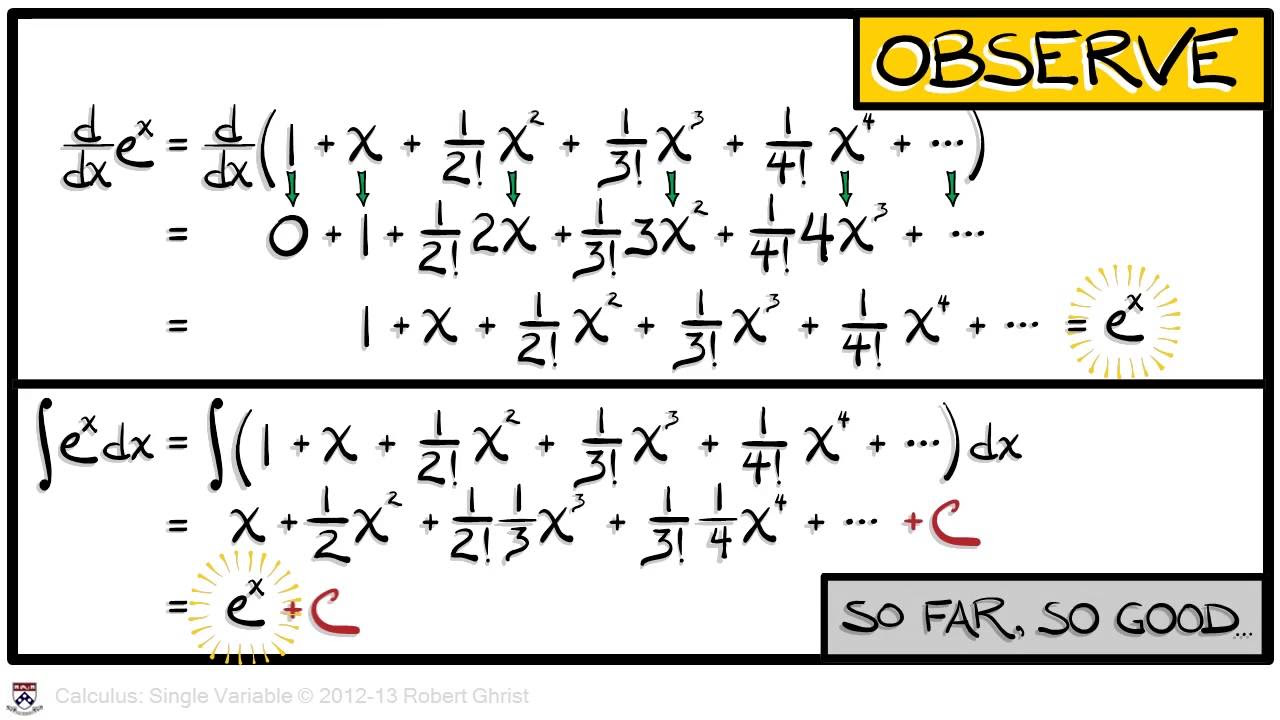
- 🧬 The professor discusses the function e^(x) and its unique property where every derivative is the same as the original function, leading to a simple and universally convergent series representation.
- 👌 The series for trigonometric functions like cos(x) and sin(x) are introduced, showing that they can be represented as infinite series of polynomial terms, which are valid for all x.
- 🔗 The connection between exponential and trigonometric functions is established through Euler's formula, e^(ix) = cos(x) + i*sin(x), demonstrating a deep relationship between these mathematical functions.
- 🎯 The special case of Euler's formula, e^(iπ) + 1 = 0, is presented as a particularly elegant mathematical identity, uniting fundamental mathematical constants in a single expression.
- 🔢 The concept of complex numbers is introduced starting with the number i, the square root of -1, and the idea that complex numbers can be represented as points in a plane, leading to the definition of complex conjugates.
- 🔄 The manipulation of complex numbers through addition, subtraction, multiplication, and division is discussed, showing that complex numbers can be used in all the ways real numbers can, with the added dimension of a complex plane.
Q & A
What is the main topic discussed by Professor Shankar in the beginning of the transcript?
-Professor Shankar begins the transcript by discussing the transition from the topic of relativity to a new topic, which involves mathematical tricks essential for understanding physics.
Why does Professor Shankar emphasize the importance of Taylor series in the context of physics?
-Professor Shankar emphasizes the importance of Taylor series because they are fundamental mathematical tools used in approximating functions, which is crucial in both physics and mathematics.
What is the purpose of introducing Taylor series to the students according to the professor?
-The professor introduces Taylor series to help students understand how to approximate functions based on their derivatives at a given point, which is a valuable skill in both physics and mathematics.
How does Professor Shankar explain the concept of approximation using the example of temperature?
-Professor Shankar uses the analogy of temperature to explain approximation. He suggests that if you know the current temperature and the rate at which it's changing, you can predict the temperature for the next day, which is a form of approximation.
What is the relevance of knowing the rate of change and its rate of change in the context of Taylor series?
-Knowing the rate of change and its rate of change is relevant in Taylor series because it allows for a better approximation of the function. The first derivative gives the slope, and the second derivative provides information about the concavity, helping to refine the approximation.
Can you provide an example of a function and its Taylor series approximation as discussed by Professor Shankar?
-One example given by Professor Shankar is the function 1 / (1 - x). The Taylor series approximation starts with 1 + x + x^2 / 2! + x^3 / 3!, and so on. This series can be used to approximate the function for values of x close to 0.
What is the significance of the factorial in the terms of the Taylor series expansion?
-The factorial in the terms of the Taylor series expansion ensures that the approximation matches the function's value, first derivative, second derivative, and so on, at the point of expansion, typically x = 0.
Why does Professor Shankar mention that the exam will be more lenient compared to the relativity problem set?
-Professor Shankar mentions that the exam will be more lenient because the problem set for relativity was challenging, with most problems being original creations rather than from the textbook, making them more difficult.
What is the connection between the Taylor series and the function e^(x) as per the professor's explanation?
-The connection is that the Taylor series for e^(x) is actually e^(x) itself, as every derivative of e^(x) is e^(x), and when expanded as a series, it remains the same function, illustrating the power of the Taylor series in function approximation.
How does Professor Shankar describe the process of finding the Taylor series for a function like cos x?
-Professor Shankar describes the process by starting with the value of the function at the origin, which for cos x is 1. Then, by taking derivatives and evaluating them at the origin, he constructs the series, which for cos x involves terms with alternating signs and increasing even powers of x, all divided by the corresponding factorial.
Outlines
😀 Introduction to Mathematical Tricks and Taylor Series
Professor Shankar begins by addressing the difficulty of the relativity problem set and reassures students that the exam will be more lenient. He then introduces the concept of mathematical tricks essential for physics, emphasizing the importance of the Taylor series. The Taylor series is presented as a method to approximate functions near a given point, x=0, by utilizing the function's derivatives at that point. The professor explains the process of creating a polynomial approximation that matches the function's value, first derivative, and second derivative at the origin.
📚 Expansion of Taylor Series and Its Applications
The professor elaborates on the Taylor series by discussing how additional derivatives provide better approximations. He demonstrates that by including higher-order derivatives, one can improve the accuracy of the approximation. The concept of factorials in the series is explained, and the professor shows how the Taylor series can sometimes exactly represent a function if all its derivatives are known. The famous example of 1/(1-x) is used to illustrate the series expansion and its convergence properties. The limitations of the Taylor series for values of x away from the origin are also discussed.
🔢 Series Representation of e^(x), cos(x), and sin(x)
The lecture continues with the series representations of exponential, cosine, and sine functions. The professor shows that e^(x) can be expanded into an infinite series involving x raised to various powers divided by factorials. He also derives the series for cos(x) and sin(x) using the properties of these functions and their derivatives. The series for these trigonometric functions are particularly useful in simplifying complex calculations and are applicable for all values of x.
🤔 Approximations in Physics and Mathematics
Professor Shankar discusses the significance of approximations in physics and mathematics. He uses the example of the energy of a particle in relativistic mechanics to illustrate how approximations can capture the essence of physical phenomena. The importance of understanding when approximations are valid and when they must be refined is emphasized. The professor also highlights that while approximations are useful, they are often superseded by more accurate theories, such as quantum mechanics for tiny objects.
🎓 Euler's Formula and Complex Numbers
The professor introduces complex numbers and their role in mathematics. He explains the concept of Euler's formula, which connects trigonometric and exponential functions. The formula e^(iπ) + 1 = 0 is presented as a beautiful mathematical identity involving key mathematical constants. The lecture also touches on the properties of complex numbers, such as their real and imaginary parts, and how they can be manipulated using algebraic operations.
📐 Polar Form of Complex Numbers and Its Utility
The lecture concludes with the polar form of complex numbers. The professor explains how complex numbers can be represented as a magnitude and an angle, which simplifies multiplication and division. The polar form is particularly useful for understanding the behavior of complex numbers in various mathematical contexts. The professor also discusses the conservation of energy in the context of simple harmonic motion and how it can be verified using the properties of trigonometric functions.
Mindmap
Keywords
💡Taylor Series
💡Exponential Function
💡Complex Numbers
💡Trigonometric Functions
💡Euler's Formula
💡Simple Harmonic Motion
💡Amplitude
💡Angular Frequency
💡Phase
💡Conservation of Energy
💡Moment of Inertia
Highlights
Introduction to mathematical tricks essential for understanding physics concepts.
Explanation of the Taylor series as a fundamental mathematical tool in physics.
The concept of using a Taylor series to approximate functions around a point where information is known.
Demonstration of how to approximate functions using derivatives and factorials in the Taylor series.
Discussion on the limitations of the Taylor series approximation and its range of validity.
Example of approximating the function 1/(1-x) using the Taylor series and its limitations.
Introduction to the exponential function e^(x) and its unique property where every derivative is e^(x).
Explanation of how the Taylor series for e^(x) converges for any value of x without restrictions.
Derivation of the series for cosine and sine functions using their derivatives and properties.
Reveal of the deep connection between trigonometric and exponential functions through Euler's formula.
Elegant representation of Euler's identity, e^(iπ) + 1 = 0, showcasing the interrelation of fundamental constants.
Introduction to complex numbers starting with the concept of i as the square root of -1.
Explanation of how complex numbers can be used to solve equations that have no real solutions.
Generalization of complex numbers into a form of z = x + iy, where x is the real part and y is the imaginary part.
Introduction to the concept of complex conjugate and its use in simplifying complex number operations.
Transformation of complex numbers into polar form re^(iθ) and its advantages in multiplication and division.
Discussion on the physical relevance of complex numbers in various fields of science and engineering.
Return to physics with a focus on small oscillations and simple harmonic motion as a ubiquitous phenomenon.
Analysis of the behavior of a mass-spring system starting from equilibrium and the application of Newton's laws.
Derivation of the differential equation for simple harmonic motion and its solution in terms of cosine function.
Explanation of the properties of simple harmonic motion, including amplitude independence from the time period.
Introduction to the concept of phase in oscillations and how it affects the solution for simple harmonic motion.
Discussion on the determination of amplitude and phase in oscillation problems to predict future positions.
Verification of the Law of Conservation of Energy in the context of simple harmonic motion.
Comparison of linear oscillation with angular oscillation, such as a twisted rod or a pendulum.
Calculation of the angular frequency for a simple pendulum and derivation of its period formula.
Consideration of the hoop oscillation problem and the challenge of finding the restoring torque and moment of inertia.
Transcripts
Browse More Related Video

Calculus Chapter 1 Lecture 3 Taylor Series

8.03 - Lect 1 - Periodic Phenomena, SHO, Complex Notation, Physical Pendulum
Calculus Chapter 1 Lecture 2 Exponentials

5. Work-Energy Theorem and Law of Conservation of Energy
Calculus Chapter 1 Lecture 6 Expansion Points

Lec 39 | MIT 18.01 Single Variable Calculus, Fall 2007
5.0 / 5 (0 votes)
Thanks for rating: