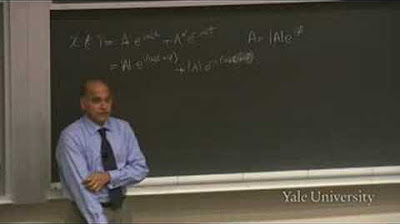To Master Physics, First Master the Harmonic Oscillator
TLDRThe video script discusses the fundamental concept of the simple harmonic oscillator, emphasizing its prevalence in physics. It explains how a block attached to a spring oscillates when displaced from its equilibrium position, illustrating the relationship between force, potential energy, and kinetic energy. The script also highlights the mathematical representation of the system using Newton's laws and the importance of understanding the system's natural frequency. Furthermore, it explores how the simple harmonic oscillator model is applicable to more complex physical systems, particularly near stable equilibrium points, and how it can be used to approximate the behavior of particles in various potentials.
Takeaways
- 📚 The simple harmonic oscillator, a block attached to a spring, is a fundamental concept in physics appearing across various fields.
- 🔧 When the spring is displaced from its equilibrium position, it exerts a restoring force proportional to the displacement (Hooke's Law).
- 📐 The motion of the block oscillating back and forth is described by sinusoidal functions and is called simple harmonic motion.
- 🌀 The natural frequency (ω) of the system is determined by the mass of the block and the spring constant, and it dictates the rate of oscillation.
- 🎲 The general solution for the block's position over time is given by x(t) = A*cos(ωt + φ) + B*sin(ωt + φ), where A and B depend on initial conditions.
- 🔄 The total mechanical energy of the system (kinetic + potential) is conserved, reflecting no net change over the oscillation cycle.
- 🏞️ The potential energy of the spring is given by U = (1/2)kx^2, and the force exerted by the spring is the negative slope of this potential energy curve.
- 📈 Taylor series expansion around a stable equilibrium point of any potential function can be approximated by a simple harmonic oscillator model for small displacements.
- 🔄 Small disturbances around stable equilibrium points in any potential lead to oscillations similar to those of a simple harmonic oscillator.
- 📊 The simple pendulum is an example where the small angle approximation allows its motion to be treated as a simple harmonic oscillator.
- 🎥 Animations and visual tools can help build intuition for the behavior of physical systems, such as the oscillations of a block on a spring or a pendulum.
Q & A
What is the simple harmonic oscillator and why is it significant in physics?
-The simple harmonic oscillator is a system consisting of a block attached to a spring. It is significant in physics because it is a fundamental concept that appears in various areas, including classical mechanics, quantum mechanics, and quantum field theory. Understanding this system is crucial for a comprehensive grasp of physics.
How does a simple harmonic oscillator behave when displaced from its equilibrium position?
-When a simple harmonic oscillator is displaced from its equilibrium position, it oscillates back and forth in a sinusoidal pattern, similar to the graph of a sine or cosine function. This motion is known as simple harmonic motion.
What is the relationship between the force exerted by the spring and the displacement from equilibrium?
-The force exerted by the spring is proportional to the displacement from the equilibrium position (x) and is given by the equation F = -kx, where k is the spring constant. The negative sign indicates that the force acts to restore the system to its equilibrium position.
What is the natural frequency of a simple harmonic oscillator, and how is it determined?
-The natural frequency (ω) of a simple harmonic oscillator is the rate at which it oscillates. It is determined by the mass (m) of the block and the spring constant (k), and is given by the formula ω = √(k/m). This frequency is inherent to the system and does not change unless the mass or spring constant is altered.
How does energy conservation manifest in the simple harmonic oscillator system?
-In the simple harmonic oscillator system, the total energy is conserved. As the block moves, its kinetic energy (KE) and potential energy (PE) in the spring change, but their sum remains constant. This is because the work done by the spring force is equal to the change in potential energy, as per the work-energy principle.
What is the role of potential energy in understanding the behavior of a particle in a potential well?
-The potential energy curve can be visualized as a hill, with the potential energy changing as the particle moves. This visualization helps in understanding the forces acting on the particle and its motion. For instance, at the bottom of the well (stable equilibrium), the particle will oscillate back and forth, similar to a simple harmonic oscillator, while at the top (unstable equilibrium), a small disturbance will cause the particle to move away.
How can the simple harmonic oscillator model be applied to more complex potentials?
-The simple harmonic oscillator model can be applied to complex potentials by identifying stable equilibrium points and analyzing the behavior of a particle near these points. By expanding the potential around a stable equilibrium using a Taylor series and keeping the quadratic term, the system can be approximated as a simple harmonic oscillator, which simplifies the analysis of the particle's motion.
What is the relationship between force, potential energy, and the equilibrium of a system?
-The force acting on a system is related to the potential energy by the equation F = -dU/dx, where F is the force, dU/dx is the slope of the potential energy curve (U) with respect to position (x). At equilibrium, the force is zero, meaning the slope of the potential energy curve vanishes, indicating a stable equilibrium where the system will remain at rest.
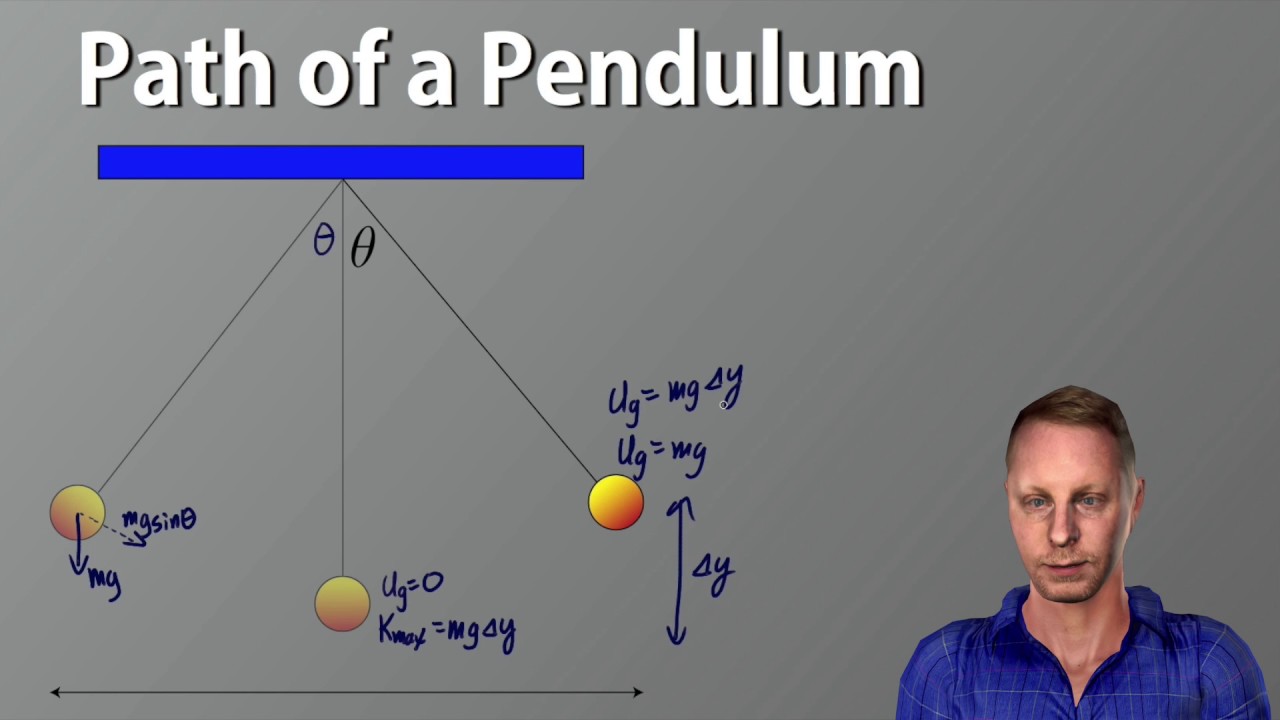
How does the concept of simple harmonic motion apply to a pendulum?
-A pendulum can be approximated as a simple harmonic oscillator when it oscillates with small angles (small angle approximation). The potential energy of the pendulum is converted into the form of a simple harmonic oscillator with an effective spring constant, and the frequency of oscillation is given by ω = √(g/l), where g is the acceleration due to gravity and l is the length of the pendulum arm.
What is the significance of the Taylor series expansion in understanding the behavior of a particle in a potential well?
-The Taylor series expansion allows us to approximate the potential energy function around a stable equilibrium point. By keeping only the quadratic term, we can model the system as a simple harmonic oscillator, which simplifies the analysis. This method is particularly useful for understanding the motion of a particle near stable equilibrium points in complex potentials.
How does the concept of simple harmonic motion help in developing intuition for more complex physical systems?
-Simple harmonic motion provides a foundational model that can be used to understand the behavior of more complex systems. By visualizing the potential energy as a hill and considering the motion of a particle near its equilibrium points, we can develop a qualitative understanding of how the particle will behave without needing to solve complex equations. This intuitive approach is valuable for predicting and explaining a wide range of physical phenomena.
Outlines
📚 Introduction to Simple Harmonic Oscillator
This paragraph introduces the simple harmonic oscillator, emphasizing its importance across various physics disciplines. It describes the basic setup of a mass attached to a spring and explains how the system oscillates when displaced from its equilibrium position. The explanation involves Newton's laws, the force exerted by the spring (proportional to the displacement), and the resulting motion that resembles sine or cosine functions. The paragraph also introduces the concept of natural frequency and the conservation of mechanical energy in the system.
🏞 Analogy of the Harmonic Oscillator with a Frictionless Hill
The second paragraph uses the analogy of a frictionless hill to develop intuition about the behavior of a particle in a potential well. It explains how a particle at the bottom of such a hill (equilibrium point) will oscillate around this point when perturbed, similar to the block on a spring. The paragraph further discusses the concept of stable and unstable equilibrium points, and how the simple harmonic oscillator potential can be used to approximate the behavior of particles near stable equilibrium points in more complex potentials. It also touches on the Taylor series expansion as a method for approximating potentials near equilibrium points.
📐 Application to the Simple Pendulum and Small Angle Approximation
The final paragraph applies the concepts discussed to the example of a simple pendulum, demonstrating how the small angle approximation allows the pendulum's motion to be treated as a simple harmonic oscillator near its equilibrium position. It outlines the process of finding the equilibrium point, determining the potential energy, and using the second derivative to find the natural frequency of oscillation. The paragraph also encourages viewers to review the accompanying notes and animations for a deeper understanding of the concepts presented.
Mindmap
Keywords
💡Simple Harmonic Oscillator
💡Equilibrium Position
💡Newton's Laws
💡Hooke's Law
💡Natural Frequency
💡Potential Energy
💡Conservation of Energy
💡Taylor Series
💡Simple Pendulum
💡Taylor Expansion
💡Restoring Force
Highlights
The simple harmonic oscillator is a fundamental system in physics, applicable across various fields from classical mechanics to quantum field theory.
The basic setup involves a block attached to a spring, which oscillates back and forth when displaced from its equilibrium position.
The oscillation of the block is sinusoidal, similar to the functions of sine or cosine, and is termed simple harmonic motion.
Newton's laws are used to understand the behavior of the system, with the spring exerting a force proportional to the displacement from equilibrium, described by Hooke's Law (F = -kx).
The equation of motion for the block can be simplified and is found to be a second-order differential equation relating the position, acceleration, and the spring constant.
The general solution to the equation of motion reveals that the block's trajectory can be described by a combination of cosine and sine functions, with parameters determined by the initial conditions.
The natural frequency of the system, denoted by omega, is determined by the spring constant and the mass of the block, and is independent of the initial conditions.
The total mechanical energy of the system remains constant, consisting of kinetic energy and potential energy stored in the spring.
The force exerted by the spring is related to the negative slope of the potential energy curve, illustrating the general relationship between force and potential energy.
The potential energy curve can be likened to a frictionless hill, which helps in developing intuition for the behavior of a particle in a general potential.
The harmonic oscillator is prevalent because systems tend to settle into stable equilibrium, and small disturbances cause oscillations around it.
Any potential energy function can be approximated by the simple harmonic oscillator potential near its stable equilibrium points by using a Taylor series expansion.
The simple pendulum is an example of a system that can be approximated by a simple harmonic oscillator under small angle approximation.
The frequency of oscillations for the pendulum is given by ω = √(g/l), which is derived from the simple harmonic oscillator model.
The simple harmonic oscillator model is a powerful tool for understanding a wide range of physical systems and their behavior under various conditions.
The concept of potential energy as a hill provides a qualitative understanding of particle behavior without needing to solve complex equations.
Animation and interactive models are useful for building intuition and visualizing the behavior of physical systems like the simple harmonic oscillator.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: