Calculus AB/BC – 6.8 Finding Antiderivatives and Indefinite Integrals: Basic Rules and Notation
TLDRIn this educational video, Mr. Bean revisits the concept of indefinite integrals, emphasizing the importance of understanding the antiderivative and general solutions. He explains how different functions can share the same derivative and introduces the notion of a particular solution, fitting specific criteria. The video covers various examples, including exponential, logarithmic, and trigonometric integrals, as well as algebraic strategies for simplifying complex integrals before solving. Mr. Bean's approach is interactive, encouraging students to pause and attempt problems on their own before revealing the solutions.
Takeaways
- 📚 The concept of indefinite integrals is being reviewed and solidified, with a focus on understanding the antiderivative and general solutions.
- 🔄 The derivative of different functions can be the same, leading to multiple antiderivative solutions, which are represented as a general solution with a '+' C' (constant).
- 🎯 The general solution for an indefinite integral includes an arbitrary constant 'C' to account for all possible antiderivatives.
- 📈 Examples of indefinite integrals include exponential functions, where the antiderivative of 'a^x' is '1/ln(a) * a^x + C' when 'a' is greater than zero.
- 🌟 Particular solutions are specific forms of the general solution that satisfy given criteria, such as passing through a specific point.
- 📊 The script provides a method for finding particular solutions by plugging in given points and solving for the constant 'C'.
- 📐 The use of logarithms and trigonometric integrals are discussed, with emphasis on the correct application of their respective rules.
- 🚫 Common mistakes are highlighted, such as incorrectly applying the natural log to expressions other than '1/x' and the importance of including absolute values when necessary.
- 🔢 The script also touches on algebraic strategies for simplifying integrals before solving them, which is especially useful in higher levels of calculus.
- 🛠️ Trigonometric derivatives are used to find the antiderivative, with a mnemonic provided to remember the signs of the results based on whether the derivative starts with 'c' or 's'.
- 📝 The importance of memorizing trigonometric derivatives for solving indefinite integrals is emphasized, as it is crucial for correctly identifying the antiderivative.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is indefinite integrals, focusing on solidifying the understanding of this mathematical concept.
What is the significance of the derivative being the same for different functions?
-The significance is that if different functions have the same derivative, it implies that their antiderivatives can be expressed in a general solution form with a variable constant 'C', illustrating the concept of a family of functions with similar behavior.
What does 'plus C' represent in the context of indefinite integrals?
-'Plus C' in indefinite integrals represents the inclusion of an arbitrary constant. Since the derivative of a constant is zero, the 'C' accounts for all possible constant values that could be part of the original function before differentiation.
How does the lesson distinguish between a general solution and a particular solution?
-A general solution includes the arbitrary constant 'C', indicating it applies to any value of the constant, while a particular solution specifies a particular value for 'C' to satisfy given criteria or initial conditions.
What is the antiderivative of 'e^x'?
-The antiderivative of 'e^x' is 'e^x + C', where 'C' is the constant of integration.
How does the lesson explain the antiderivative of 'a^x' where 'a' is a positive number?
-The lesson explains that the antiderivative of 'a^x' is '1/(natural log of a) * a^x + C'. This is derived by recognizing that the derivative of this expression would give you back the original function 'a^x'.
What is the role of absolute value in the integral of '1/x'?
-The absolute value is used in the integral of '1/x' to ensure that the logarithm function is defined for all positive values of 'x', as the logarithm is not defined for negative values or zero.
How does the lesson handle trigonometric integrals?
-The lesson explains that the integral of trigonometric functions like sine and cosine can be found by using the inverse trigonometric functions. For example, the integral of 'secant^2(x)' is 'tan(x)', and the integral of 'tan(x)' is 'secant(x)'.
What is the strategy for dealing with complex integrals like '3x^2 / (x + x^2 - 1)'?
-The strategy involves separating the rational functions in the denominator and integrating each term separately, which simplifies the process of finding the antiderivative.
What is the purpose of memorizing trigonometric derivatives?
-Memorizing trigonometric derivatives is crucial for quickly identifying the antiderivative of trigonometric functions, which is essential for solving indefinite integral problems involving trigonometry.
How does the lesson conclude?
-The lesson concludes by encouraging students to practice and master the concepts of indefinite integrals, and to apply the strategies learned for solving more complex integral problems in higher levels of calculus.
Outlines
📚 Introduction to Indefinite Integrals
This paragraph introduces the concept of indefinite integrals, contrasting them with definite integrals. It explains that indefinite integrals involve finding the antiderivative of a function, which can have multiple answers represented by the general solution with a '+' C' (constant). The paragraph also distinguishes between particular and general solutions, providing examples of both. It sets the stage for the lesson by reviewing the derivative of three functions and their identical antiderivative, emphasizing the importance of understanding the underlying concepts before diving into examples.
📈 Exponential and Logarithmic Functions
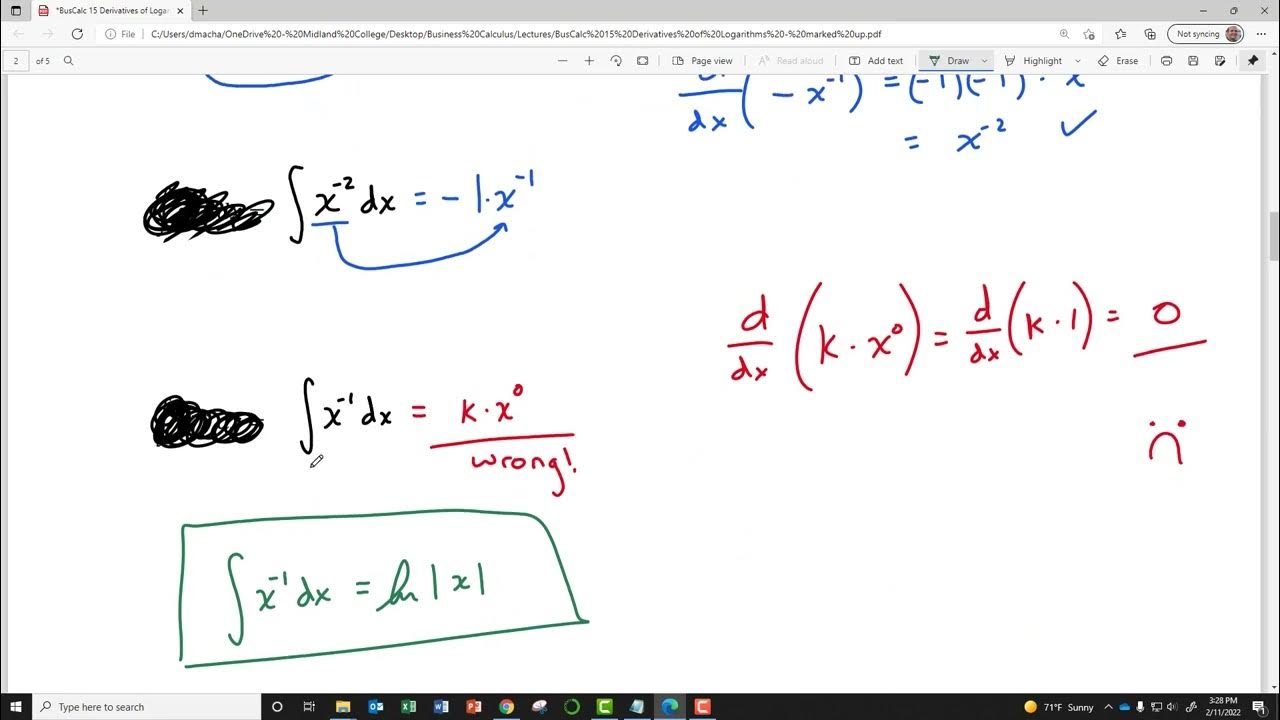
This section delves into the antiderivatives of exponential and logarithmic functions. It starts with the straightforward case of e^x, whose antiderivative is itself plus a constant. The paragraph then tackles a trickier example involving a^x, where 'a' is a positive number. The antiderivative in this case is 1/ln(a) * a^x + C. The explanation includes a reminder about the domain restrictions of logarithmic functions and the necessity of absolute values. The section also covers the antiderivatives of 1/x and 1/x^2, clarifying common mistakes and emphasizing the importance of understanding the power rule in reverse.
📊 Trigonometric Integrals
This paragraph focuses on the antiderivatives of trigonometric functions. It reviews the basic derivatives of sine and cosine, then moves on to more complex trigonometric integrals such as secant squared and tangent. The explanation includes mnemonics for remembering the signs of trigonometric derivatives and antiderivatives, as well as the process of finding particular solutions by plugging in given coordinates. The paragraph emphasizes the importance of memorizing trigonometric derivatives for successfully solving these types of integrals.
🧩 Algebraic Strategies for Integrals
The final paragraph discusses algebraic strategies for simplifying integrals before solving them, a technique particularly useful in higher levels of calculus. It provides examples of separating rational functions and manipulating algebraic expressions to make the integral easier to handle. The section concludes with a comprehensive summary of the lesson's content, encouraging students to apply their knowledge of indefinite integrals in practice.
Mindmap
Keywords
💡Indefinite Integrals
💡Derivative
💡Antiderivatives
💡General Solution
💡Particular Solution
💡Exponential Functions
💡Logarithms
💡Trigonometric Integrals
💡Algebraic Strategies
💡Inverse Trigonometric Functions
Highlights
Introduction to indefinite integrals and their importance in solidifying understanding of derivatives.
Derivative of functions f(x) = x^2, f(x) = x, and f(x) = 1/x, all resulting in f'(x) = 2x, demonstrating that different functions can have the same derivative.
Explanation of antiderivatives and the concept of a general solution, denoted by the 'plus C'.
Difference between indefinite integrals and definite integrals, with the latter involving area under a curve between two points.
Example of finding the indefinite integral of e^x, resulting in e^x + C as the general solution.
Discussion on the indefinite integral of a^x, where 'a' is a positive number, and the derivation of the general solution 1/ln(a) * a^x + C.
Particular solution for the integral of a^x where x=0 and y=4, leading to the function f(x) = e^x - 2/3 * x^3 + C.
Explanation of the absolute value in the integral of 1/x, due to the vertical asymptote and the domain restrictions of the logarithm function.
Antiderivatives of 1/x^2, resulting in the natural log of |x| + C, and the common mistake of omitting the absolute value.
Process of finding a particular solution for the integral of 2 * ln|x| + 6/x^2, using given coordinates to determine the constant C.
Review of trigonometric integrals, including the antiderivative of secant squared as tangent x, and the use of trigonometric derivatives to find antiderivative functions.
Strategy for dealing with inverse trigonometric derivatives, such as recognizing the structure of the integral to find the antiderivative as secant^(-1)x + C or arcsec(x) + C.
Algebraic strategies for simplifying integrals before solving, such as separating rational functions and simplifying complex expressions.
Example of simplifying the integral of (3x^2 + x + 2)/(x^2 - 1) by separating terms and simplifying, leading to a more manageable antiderivative.
Final encouragement for mastering the concepts of indefinite integrals and looking forward to the next lesson.
Transcripts
Browse More Related Video

Calculus AB/BC – 7.2 Verifying Solutions for Differential Equations

Calculus BC – 6.13 Evaluating Improper Integrals

Business Calculus - Math 1329 - Section 5.1 - Indefinite Integration & Differential Equations

Calculus AB/BC – 7.7 Particular Solutions using Initial Conditions and Separation of Variables

Precalculus Final Exam Review
BusCalc 15 Derivatives of Logarithms
5.0 / 5 (0 votes)
Thanks for rating: