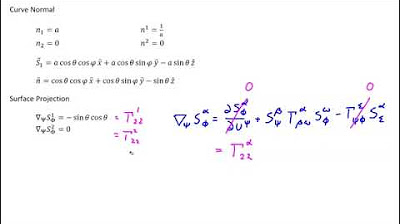Video 99 - Holonomy Part 2
TLDRThis video script delves into tensor calculus, deriving an expression akin to the Gauss-Bonnet theorem. It explores the parallel transport of a vector around a small parallelogram defined by vectors du Alpha and dv Beta. The script explains the incremental changes in the vector due to curvature, highlighting that when the Riemann tensor is zero, indicating flatness, the vector remains unchanged. The final tensor equation quantifies how much a vector changes when transported around an area, emphasizing the relationship between surface curvature and vector change.
Takeaways
- 📚 The video discusses deriving a tensor calculus expression equivalent to the Gauss-Bonnet theorem.
- 📏 It starts with a small parallelogram defined by vectors \( \mathbf{du}^\alpha \) and \( \mathbf{dv}^\beta \) to explore vector transport.
- 🔄 The process of parallel transporting a vector \( \mathbf{T} \) around the parallelogram in a counterclockwise direction is explained.
- 🔠 The change in the vector is expressed in terms of a bilinear form involving the Christoffel symbols.
- 📈 The Christoffel symbols at a new point \( P1 \) are expanded using a Taylor series, considering only the first two terms for the infinitesimal displacement.
- 🔢 The value of the vector \( \mathbf{T} \) at \( P1 \) is found by adding the infinitesimal change to its value at \( P0 \).
- ➗ The distributive property is used to expand the expressions, simplifying and combining like terms.
- 🔄 The process is mirrored for transport from \( P2 \) to \( P3 \) and back to \( P0 \), with variables and indices swapped.
- 🔗 The first-order terms cancel out when considering the complete loop, leaving only second-order terms.
- 🌐 The final expression for the change in the vector is related to the Riemann-Christoffel tensor, quantifying the effect of curvature on vector transport.
- 📉 When the Riemann tensor is zero, indicating a flat surface, the vector remains unchanged after parallel transport in a closed loop.
Q & A
What is the main topic discussed in video 99 of tensor calculus?
-The main topic discussed is the derivation of a tensor calculus expression equivalent to the Gauss-Bonnet theorem, focusing on the parallel transport of a vector around a parallelogram on a curved surface.
What is the significance of the small parallelogram defined by two vectors du Alpha and dv Beta?
-The small parallelogram represents a small area on a surface where the vector is being parallel transported, and the vectors du Alpha and dv Beta define the directions along which the transport occurs.
What is parallel transport and why is it important in this context?
-Parallel transport is the process of moving a vector along a path on a surface in such a way that it remains parallel to itself at the starting point. It is important because it allows us to understand how vectors change when moved around a closed loop on a curved surface.
What role does the Christoffel symbol play in the derivation?
-The Christoffel symbol is used to express the change in the vector during parallel transport from one point to another, accounting for the curvature of the surface at different points.
Why is the Taylor series expansion used in the derivation?
-The Taylor series expansion is used to approximate the value of the Christoffel symbol at a point P1, which is different from its value at point P0, by considering the change in the coordinate value and the displacement.
What is the significance of retaining only the first two terms of the Taylor series?
-The first two terms of the Taylor series are retained because they represent the most significant changes in the vector during parallel transport. Higher-order terms are infinitesimal and can be ignored in the limit as they approach zero.
How does the video script relate the change in the vector to the curvature of the surface?
-The script shows that the change in the vector during parallel transport around a closed loop is directly related to the Riemann Christoffel tensor, which quantifies the curvature of the surface.
What is the final expression derived for the change in the vector DT Lambda?
-The final expression for the change in the vector DT Lambda is given by the Riemann Christoffel tensor contracted with the vector T Omega and the transporting vectors du Alpha and dv Beta.
What does it mean when the Riemann tensor is zero?
-When the Riemann tensor is zero, it indicates that the surface is flat, and the vector remains constant when parallel transported in a closed loop, as there is no curvature to cause a change.
How does the derived tensor equation relate to the Gauss-Bonnet theorem?
-The derived tensor equation quantifies the change in a vector when transported around a small area on a surface, which is analogous to the Gauss-Bonnet theorem's statement that the change is related to the product of the surface's curvature and the enclosed area.
Outlines
📚 Derivation of Tensor Calculus Expression for Vector Parallel Transport
In this paragraph, the video script discusses the derivation of a tensor calculus expression that parallels the Gauss-Bonnet theorem. The focus is on the parallel transport of a vector around a small parallelogram defined by two vectors, du Alpha and DV beta. The process involves moving the vector from point P0 to P1, then to P2, P3, and back to P0 in a counterclockwise direction. The script explains the use of a bilinear form to represent the change in the vector during parallel transport and introduces the Christoffel symbol, which varies at different points. The Taylor series is employed to approximate the change in the Christoffel symbol and the vector T at point P1, considering only the first two terms of the series due to the infinitesimal nature of the displacement.
🔍 Expanding and Simplifying the Tensor Expression for Parallel Transport
This section of the script continues the exploration of vector parallel transport by expanding the expressions for the change in the vector as it moves from P1 to P2. The script uses the distributive property to break down the expressions into individual terms, highlighting the presence of first, second, and third order terms. It emphasizes the importance of retaining terms up to the second order due to their significance in comparison to higher order terms, which are negligible. The script then proceeds to rename indexes to simplify the expressions and explains the process of combining the changes from P0 to P1 and P1 to P2 to find the overall change from P0 to P2.
🔗 Completing the Parallel Transport and Relating to Surface Curvature
The final paragraph of the script concludes the process of parallel transport by considering the transport from P2 to P3 and back to P0. It cleverly points out that the transport in the opposite direction can be used to achieve the same result as going around the entire parallelogram. The script shows how to derive the change in the vector from P0 to P3 to P2 by swapping certain variables and indexes. After adding and subtracting the expressions, the first order terms cancel out, leaving only the second order terms, which are crucial. The script then groups these terms and relates the final expression to the Riemann Christoffel tensor, drawing a connection to the Gauss-Bonnet theorem. It concludes by explaining that the change in the vector during parallel transport around a closed loop is directly related to the surface's curvature and the enclosed area, with no change occurring if the surface is flat.
Mindmap
Keywords
💡Tensor Calculus
💡Gauss's Theorema Egregium
💡Parallel Transport
💡Christoffel Symbols
💡Riemann Curvature Tensor
💡Infinitesimal
💡Taylor Series
💡Distributive Property
💡Covariant Derivative
💡Flat Manifold
💡Curvature
Highlights
Derivation of a tensor calculus expression equivalent to the Gauss-Bonnet theorem.
Introduction of a small parallelogram defined by vectors du Alpha and dv beta.
Parallel transport of a vector T around a parallelogram in a counterclockwise direction.
Use of bilinear form to describe the change in vector T during parallel transport.
Differentiation between the values of the Christoffel symbol at points P0 and P1.
Application of the Taylor series to expand the Christoffel symbol at point P1.
Explanation of ignoring higher order terms in the Taylor series due to their infinitesimal nature.
Calculation of the vector T Sigma at point P1 using the change in vector T from P0 to P1.
Use of the distributive property to expand the expressions for individual terms.
Identification of first, second, and third order terms in the expanded expression.
Retention of second order terms and omission of the third order term for simplification.
Renaming of indexes to consolidate terms and prepare for the addition of expressions.
Addition of expressions for vector transport from P0 to P2 and P1 to P2.
Discovery that first order terms cancel out, leaving only second order terms.
Expression for vector change when transported from P0 to P3 to P2 by swapping variables.
Final expression for the change in vector T involving the Riemann Christoffel tensor.
Interpretation of the final tensor expression in relation to the curvature of the surface.
Conclusion that when the Riemann tensor is zero, the vector remains constant indicating flatness.
Summary of the video's derivation and its equivalence to the Gauss-Bonnet theorem in tensor calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: