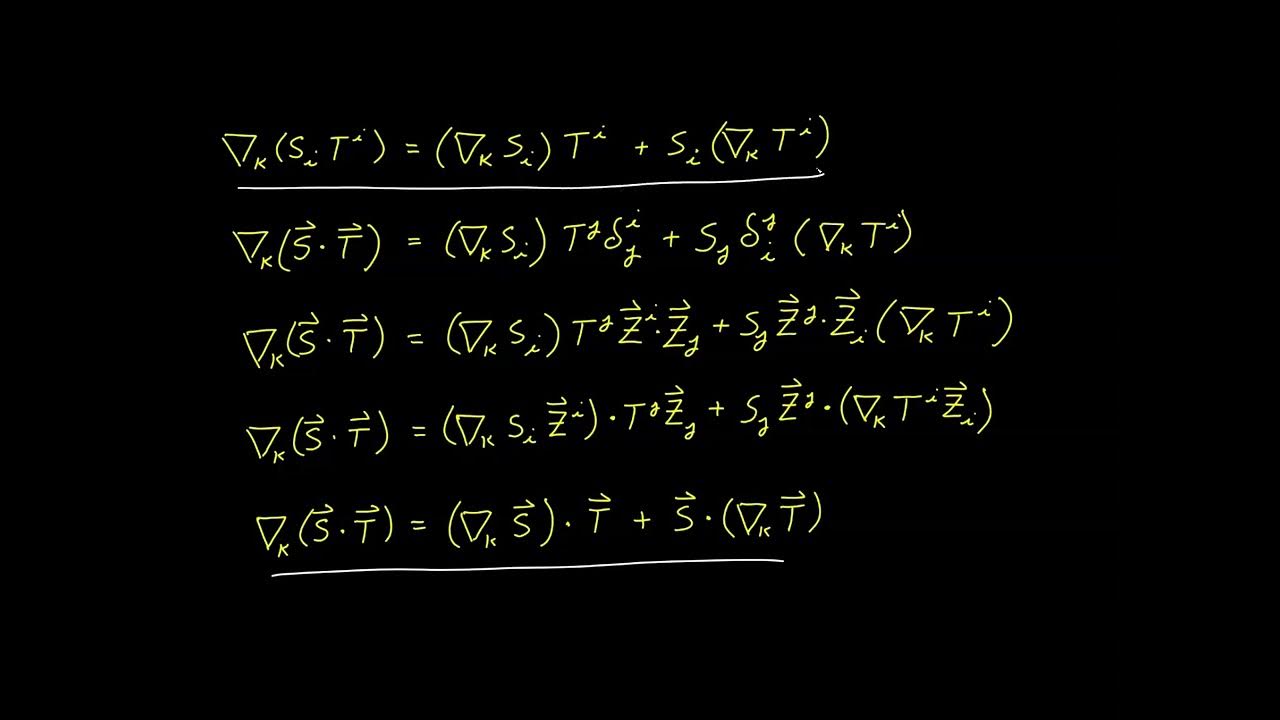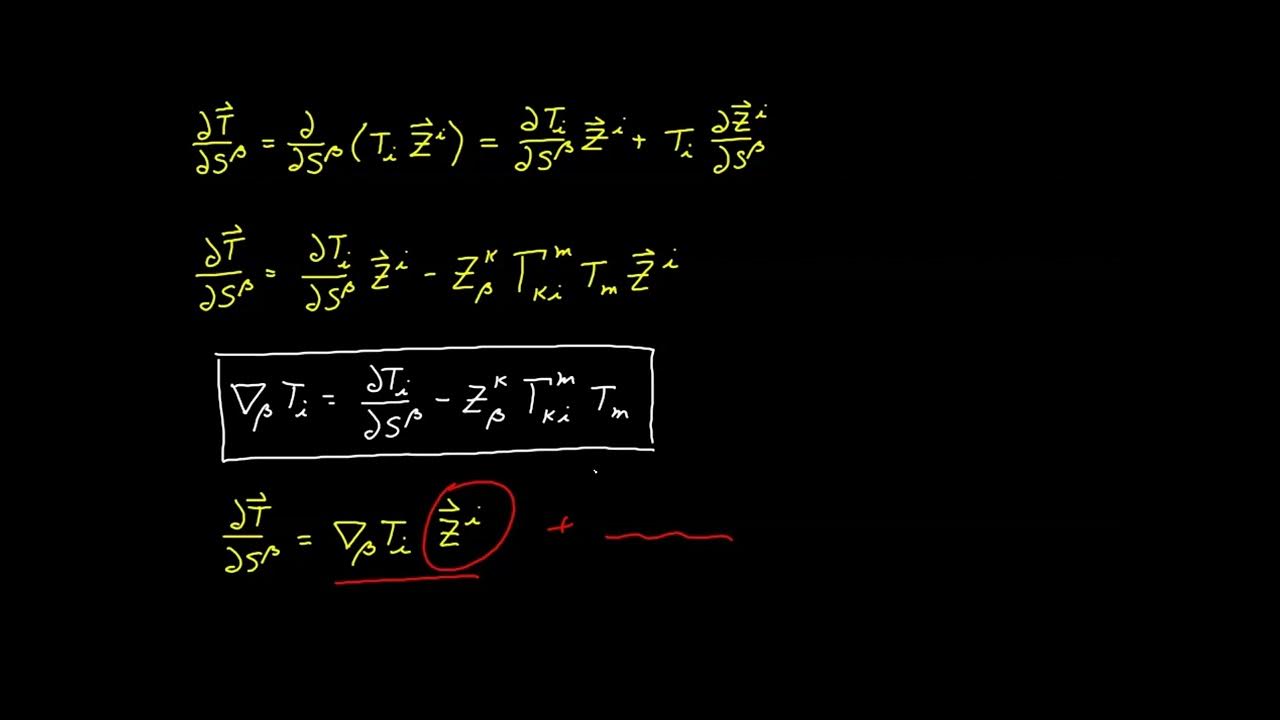Video 85 - Commutation for Higher Rank Tensors

Tensor Calculus

5 Jun 202223:11

EducationalLearning

32 Likes 10 Comments

TLDRThis video, part of a tensor calculus series, explores the application of the commutative operator to various mathematical entities. It delves into the effects on covariant vector components, scalar functions, and higher-rank tensors, highlighting the anti-symmetry of the Riemann tensor and the commutation of the covariant derivative with scalar functions and invariant expressions. The video also examines the commutative operator's adherence to the sum and product rules, concluding with a general method for applying the operator to tensors of any rank, emphasizing the importance of free surface indexes in the process.

Takeaways

📚 The video extends the analysis of the commutative operator to include all vector forms, scalar functions, and higher-rank tensors, building upon the introduction of the Riemann tensor in a previous video.
🔍 When applying the commutative operator to a covariant vector component, the process involves lowering the index and using the covariant metric tensor, with the covariant metric tensor being metronomic with respect to the covariant derivative.
🔄 The commutative operator, when applied to a scalar function, results in zero, indicating that the operation commutes with respect to scalar functions and any invariant object.
📉 Applying the commutative operator to a vector with an ambient index also results in zero, due to the metronomic property of the ambient basis vector with respect to the covariant derivative.
❌ The covariant derivative does not commute when the vector is expressed in terms of a surface index, necessitating the use of the Riemann tensor to express the non-commutative result.
🔢 The commutative operator obeys the sum rule, meaning it can be applied to each term of a sum separately, with the results being additive.
📈 The product rule is also followed by the commutative operator, allowing it to be applied to each factor in a product, with the operation being distributive over the product of terms.
📝 The script provides a general pattern for applying the commutative operator to tensors of any rank, focusing on free surface indexes and their positions (upper or lower) to determine the sign and direction of contractions.
📉 For tensors of any rank, the commutative operator results in zero when a contraction forms a scalar function, as scalar functions are invariant under covariant differentiation.
🔑 The key to understanding the commutative operator's application to tensors lies in identifying free surface indexes and applying the appropriate contractions, with attention to their position and sign.
🔍 The video script serves as a comprehensive guide to the application of the commutative operator in tensor calculus, emphasizing the importance of index positions and the properties of tensors under covariant differentiation.

Q & A

What is the main topic of this video in the series on tensor calculus?
-The main topic of this video is to extend the analysis of the commutative operator to all vector forms, scalar functions, and tensors of higher rank.
What was the Riemann tensor introduced by in the previous video?
-The Riemann tensor was introduced by applying the commutative operator to a contravariant vector component in video 82.
What happens when the commutative operator is applied to a covariant vector component?
-When the commutative operator is applied to a covariant vector component, the index is lowered into the lower position by multiplying both sides by the covariant metric tensor.
Why is it not necessary to expand the entire expression when applying the commutative operator to a covariant vector component?
-It is not necessary because the process can be simplified by lowering the index and utilizing the properties of the covariant metric tensor and the Riemann tensor, avoiding the need for full expansion.
What property of the covariant metric tensor allows it to work its way across operations in tensor calculus?
-The covariant metric tensor is metronomic with respect to the covariant derivative, which allows it to affect the target object across operations without alteration.
What is the result of applying the commutative operator to a scalar function?
-The result of applying the commutative operator to a scalar function is zero, as the operation commutes with respect to a scalar function.
Does the commutative operator applied to an invariant object result in zero?
-Yes, the commutative operator applied to any invariant object, such as a straight vector or a full contraction, results in zero.
How does the covariant derivative behave when applied to a vector with an ambient index?
-The covariant derivative commutes with respect to a vector expressed in terms of an ambient index, resulting in zero due to the metronomic property of the ambient basis vector with respect to the covariant derivative.
What are the general rules for applying the commutative operator to a tensor of any rank?
-For a tensor of any rank, the commutative operator is applied by looking at each free surface index. For each upper position index, a positive term with a contraction from high to low is added. For each lower position index, a negative term with a contraction from low to high is included.
Does the commutative operator obey the sum rule and the product rule?
-Yes, the commutative operator obeys both the sum rule and the product rule, applying the operation to a sum or product of terms is equivalent to applying the operation to each term separately and then combining the results.
What should be done when forming a contraction with the commutative operator in tensor expressions?
-When forming a contraction with the commutative operator, any resulting scalar function or factors with ambient indexes should be ignored, as they contribute zero to the final result.

Outlines

00:00

📚 Tensor Calculus: Commutative Operator on Vector Forms

This paragraph introduces the extension of the analysis of the commutative operator to various vector forms, scalar functions, and higher rank tensors. It revisits the Riemann tensor introduced in video 82 and explores the effects of applying the commutative operator to covariant vector components. The process involves lowering the index with the covariant metric tensor and adjusting for the anti-symmetry of the Riemann tensor. The result is compared with the application to contravariant vector components, highlighting the differences in sign and contraction direction.

05:01

🔍 Commutative Operator on Scalar Functions and Invariant Objects

The second paragraph delves into the application of the commutative operator to scalar functions, revealing that it results in zero due to the commutative property of the covariant derivative. This property is extended to invariant objects such as straight vectors and full contractions, indicating that any expression without free indexes yields a zero result when the commutative operator is applied. The paragraph also discusses the application to vectors with ambient indexes, demonstrating that the covariant derivative commutes in these cases as well.

10:02

🔄 Commutative Operator's Adherence to Sum and Product Rules

Here, the script investigates whether the commutative operator follows the sum and product rules. Through a step-by-step process, it is shown that applying the commutative operator to a sum of terms is equivalent to applying it to each term individually and then summing the results. Similarly, the product rule is obeyed, where the operation on a product of terms is akin to applying it to each factor while keeping the other constant. The paragraph concludes that these properties hold true for tensors of any rank, providing a foundational understanding for further applications.

15:02

📘 General Application of the Commutative Operator to Tensor Expressions

The fourth paragraph expands on the general application of the commutative operator to tensor expressions of any rank. It outlines the process of identifying free surface indexes and forming contractions accordingly, with positive terms for upper position indexes and negative terms for lower position indexes. The paragraph also addresses the cancellation of terms when a contraction forms a scalar function and emphasizes the importance of ignoring ambient indexes in the operation.

20:04

🔚 Recap and Conclusion of Commutative Operator Principles

In the final paragraph, a recap of the entire video's content is provided, summarizing the key findings and principles related to the commutative operator. It reiterates that the covariant derivative commutes in all cases except when dealing with surface indexes in the upper or lower positions. The paragraph also restates the adherence of the commutative operator to the sum and product rules and concludes with a general pattern for applying the operator to tensors of any rank, reinforcing the understanding of tensor calculus concepts.

Mindmap

Keywords

💡Tensor Calculus

Tensor calculus is a branch of mathematics that deals with the manipulation of tensors, which are mathematical objects generalizing scalars, vectors, and higher-dimensional arrays. In the context of the video, tensor calculus is used to analyze the properties of spacetime in the theory of general relativity. The script extends the analysis of the commutative operator to various tensor forms, indicating its importance in understanding the fundamental operations within this field.

💡Commutative Operator

The commutative operator is a mathematical function that, when applied, results in the same output regardless of the order of the operands. In the video, the commutative operator is applied to different mathematical objects such as vectors, scalar functions, and higher-rank tensors to explore how the covariant derivative behaves under different conditions, which is central to the theme of the video.

💡Riemann Tensor

The Riemann tensor is a key concept in differential geometry and general relativity, describing the curvature of spacetime. In the script, the Riemann tensor is introduced as part of the process of applying the commutative operator to a contravariant vector component, highlighting its role in expressing the non-commutativity of the covariant derivative when applied to tensors with surface indices.

💡Covariant Vector Component

A covariant vector component is a component of a vector in a coordinate system that uses covariant basis vectors. In the video, the script discusses applying the commutative operator to covariant vector components and the process of lowering an index, which involves multiplying by the covariant metric tensor, to explore the behavior of these components under the operator.

💡Covariant Metric Tensor

The covariant metric tensor is a fundamental object in the study of curved spaces, defining the inner product of vectors in a coordinate-free manner. In the script, it is mentioned as being used to lower an index, which is a crucial step in the process of applying the commutative operator to covariant vector components.

💡Scalar Function

A scalar function is a mathematical function that associates a scalar (a single numerical value) to each point in its domain. In the video, the commutative operator is applied to a scalar function, and it is found that the result is zero, indicating the operator's property of commuting with scalar functions.

💡Covariant Derivative

The covariant derivative is a generalization of the derivative to curved spaces, providing a way to differentiate vector fields and other tensors. In the script, the covariant derivative is discussed in relation to the commutative operator, and it is shown that it commutes with scalar functions and vectors with ambient indices, but not with vectors with surface indices.

💡Ambient Index

An ambient index is an index that is not associated with the intrinsic properties of a tensor but is rather related to the surrounding space or 'ambient' space. In the video, the script explains that the commutative operator, when applied to a vector with an ambient index, results in zero, which is a significant finding in the analysis.

💡Product Rule

The product rule is a fundamental principle in calculus that states how the derivative of a product of functions is computed. In the context of the video, the product rule is applied to the commutative operator, demonstrating that the operator obeys this rule, which is crucial for understanding how to apply the operator to more complex expressions.

💡Sum Rule

The sum rule in calculus states that the derivative of a sum of functions is the sum of the derivatives of the individual functions. In the video, the script shows that the commutative operator adheres to the sum rule, meaning that applying the operator to a sum of tensors is equivalent to applying it to each tensor separately.

💡Surface Index

A surface index is an index that is intrinsic to a tensor and is associated with the properties of the tensor itself, as opposed to an ambient index. In the video, the script discusses how the covariant derivative does not commute with tensors that have surface indices, which is a key point in understanding the limitations of the commutative property in tensor calculus.

Highlights

Introduction of extending the analysis of the commutative operator to all vector forms, scalar functions, and higher-rank tensors.

Explanation of applying the commutative operator to a covariant vector component and the process of lowering the index.

Discussion on the anti-symmetry of the Riemann tensor and its effect on the commutative operator's application.

Comparison of results when the index is in the upper versus lower position in the commutative operation.

Application of the commutative operator to a scalar function and the discovery that it results in zero.

Generalization that the commutative operator results in zero for any invariant object, such as a straight vector or full contraction.

Analysis of applying the commutative operator to a vector with an ambient index and the resulting zero outcome.

Demonstration that the covariant derivative commutes with respect to a scalar function or any other invariant expression.

Investigation of the commutative operator's adherence to the sum rule and its application to a sum of terms.

Examination of the product rule with the commutative operator and its application to a product of terms.

Expansion of the expression using the commutative operator and the cancellation of terms due to the presence of ambient indexes.

Formation of contractions using the Riemann tensor in the context of the commutative operator's application.

General pattern for applying the commutative operator to tensors of any rank, focusing on free surface indexes.

Recap of the commutative operator's behavior when applied to different mathematical objects and its implications.

Conclusion emphasizing the commutative operator's properties, including its adherence to the sum and product rules.

Final summary of the rules for applying the commutative operator to tensors, highlighting the importance of free surface indexes.

Transcripts

Browse More Related Video

Video 37 - Metrinilic Property - Part 1

Video 72 - Surface Covariant Derivative for Non Tangent Vectors

Video 36 - Covariant Derivative Properties

Introduction to Tensors

Tensor Operations: Contractions, Inner Products, Outer Products

Video 73 - Surface Covariant Derivative Properties

Related Tags

Tensor Calculus Commutative Operator Riemann Tensor Covariant Derivative Vector Analysis Higher-Rank Tensors Mathematical Physics Advanced Calculus Differential Geometry Mathematics Education