Tensor Calculus 2: The Two Conflicting Definitions of the Gradient

MathTheBeautiful

13 Feb 201436:05

EducationalLearning

32 Likes 10 Comments

TLDRThis script delves into the concept of the gradient in multivariable calculus, exploring its geometric interpretation as a vector pointing in the direction of the greatest rate of increase of a function. It contrasts this with the analytical definition involving partial derivatives and Cartesian coordinates. The discussion highlights the limitations of the analytical definition when applied to non-Cartesian coordinate systems, emphasizing the need for a coordinate-independent expression. The script also introduces the directional derivative and its relationship to the gradient, illustrating how the gradient dictates the rate of change in all directions.

Takeaways

📚 The script discusses the concept of the gradient in multivariable calculus, focusing on its geometric interpretation and its relation to partial derivatives.
🧭 It introduces two definitions of the gradient: one as the vector pointing in the direction of the greatest increase of a function, and the other as a pair of partial derivatives in Cartesian coordinates.
🌡️ An example using temperature as a function in a room is given to illustrate the concept of the gradient without the need for coordinates, emphasizing the geometric nature of the gradient.
🤔 The script raises questions about the limitations of defining the gradient solely with partial derivatives and how it might differ in various coordinate systems.
📏 The importance of distinguishing between a vector and a pair of numbers is highlighted, especially when considering coordinate systems other than Cartesian.
🔍 The script points out the failure of the naive attempt to define the gradient in non-Cartesian coordinate systems, such as polar coordinates, without proper adjustments.
📐 It discusses the need to 'marry' algebra with geometry to properly express the gradient in analytical terms that are invariant across different coordinate systems.
🔄 The concept of stretching or altering the Cartesian coordinate system is explored to demonstrate how the gradient's analytical expression can fail to remain consistent.
📈 The script suggests normalizing the gradient expression to make it work for all stretched coordinate systems, which involves adjusting the denominator to account for changes in coordinate vectors.
📘 The importance of the directional derivative is emphasized, and it is shown that the gradient, when dotted with a unit vector in any direction, gives the directional derivative.
🔑 The script concludes with the insight that knowing the gradient allows one to determine all directional derivatives, highlighting the gradient's role as a fundamental property of a function in space.

Q & A

What are the two definitions of the gradient mentioned in the script?
-The first definition is that the gradient is the vector that points in the direction of the greatest increase of the function, with its magnitude equal to the rate of increase of the function. The second definition is that the gradient is a pair of partial derivatives in Cartesian coordinates.
Why is the first definition of the gradient considered geometrically invariant?
-The first definition is considered geometrically invariant because it does not require the use of any coordinates to determine the vector, making it consistent across different coordinate systems.
What is the problem with defining the gradient as a pair of numbers in Cartesian coordinates?
-The problem is that it's unclear whether the gradient should be considered as a pair of numbers or as a vector. This distinction becomes problematic when trying to generalize the definition to other coordinate systems.
What is the significance of the domain of the function in the context of the gradient?
-The domain of the function is significant because it's where all the interesting vectors, including the gradient, live. It's more useful to think about the domain rather than the graph when considering the gradient.
How does the script suggest measuring the gradient in a room with varying temperature?
-The script suggests imagining the room as the domain and picking a point, then sampling all surrounding points to find where the increase in temperature is the greatest. This process involves calculating the rate of change and taking a limit as the sampling area gets smaller.
Why is the expression involving partial derivatives not a correct definition of the gradient in all coordinate systems?
-The expression involving partial derivatives fails when applied to non-Cartesian coordinate systems, such as polar coordinates, or even stretched Cartesian coordinates, because it does not account for the changes in the coordinate vectors and the scaling of the derivatives.
What is the proposed solution to fix the expression for the gradient to work in all coordinate systems?
-The proposed solution is to normalize the gradient vector by dividing by the scaling factors of the coordinate system, which ensures that the expression works for both Cartesian and stretched Cartesian coordinate systems.
What is the importance of the directional derivative in understanding the gradient?
-The directional derivative is important because it shows the rate of change of a function in a specific direction. It helps to understand that the gradient vector points in the direction of the greatest increase and its magnitude represents the rate of this increase.
How does the script connect the gradient with the rate of increase of a function?
-The script connects the gradient with the rate of increase by showing that the directional derivative in the direction of the gradient is equal to the magnitude of the gradient, which is the rate of increase of the function.
What is the challenge in defining the gradient in polar coordinates or other non-Cartesian coordinate systems?
-The challenge is to find an expression for the gradient that works in these systems, taking into account the different coordinate vectors and the way partial derivatives behave in these systems, without relying on the specific properties of Cartesian coordinates.

Outlines

00:00

📚 Introduction to Gradient and Coordinate Systems

The script begins with an introduction to the concept of the gradient, discussing its two primary definitions: one as the vector pointing in the direction of the greatest increase of a function with its magnitude equal to the rate of that increase, and the other as a pair of partial derivatives in Cartesian coordinates. The instructor emphasizes the desire to move beyond Cartesian coordinates and to explore how the gradient can be defined in various coordinate systems. The discussion also touches on the geometric interpretation of the gradient without the use of coordinates, using the analogy of temperature variation in a room.

05:01

🔍 Deep Dive into Gradient Definitions and Coordinate Systems

This paragraph delves deeper into the definitions of the gradient, highlighting the challenges of expressing the gradient in different coordinate systems. The instructor points out that while the first definition of the gradient is invariant and does not depend on coordinates, the second definition, involving partial derivatives, does. The discussion aims to find a way to connect the geometric concept of the gradient with its algebraic expression in Cartesian coordinates and the need to adapt this expression for other coordinate systems such as polar or spherical.

10:02

🌐 Cartesian Coordinates and the Gradient Expression

The script continues with an exploration of how to express the gradient in Cartesian coordinates, using temperature as a function of x and y to illustrate the concept. The instructor discusses the naive approach to defining the gradient with partial derivatives and the issues that arise when attempting to generalize this definition to other coordinate systems. The importance of understanding how coordinate vectors and the function's behavior change when transitioning between coordinate systems is emphasized.

15:03

🔄 The Impact of Stretched Coordinate Systems on Gradient Expression

In this paragraph, the instructor discusses the effects of stretched or affine coordinate systems on the gradient expression. Using an example of a stretched Cartesian coordinate system, it is shown that the naive gradient expression does not hold when the coordinate lines are not one unit apart. The instructor demonstrates that the gradient expression can vary significantly when the coordinate system is altered, leading to a failure in expressing the gradient consistently across different systems.

20:05

🔍 Correcting the Gradient Expression for Stretched Coordinates

The script addresses the need to correct the gradient expression to make it work for all stretched coordinate systems. The instructor suggests normalizing the coordinate vectors and adjusting the expression to account for changes in the coordinate system. The discussion leads to a revised expression that works for Cartesian and stretched Cartesian coordinate systems, highlighting the importance of finding an expression that is invariant under coordinate transformations.

25:07

📐 Exploring Directional Derivatives and Gradient in Cartesian Coordinates

This paragraph focuses on the concept of directional derivatives and how they relate to the gradient in Cartesian coordinates. The instructor explains the process of finding the directional derivative in a given direction using the chain rule and the dot product of the gradient and the unit vector in the direction of interest. The discussion reveals the simplicity and power of the relationship between the gradient and directional derivatives, showing that knowing the gradient allows for the determination of the rate of change in any direction.

30:11

🧭 Generalizing Gradient Expression for All Coordinate Systems

The final paragraph of the script discusses the challenge of generalizing the gradient expression to work in all coordinate systems. The instructor introduces the concept of a coordinate basis and the need to define it in arbitrary coordinate systems. The goal is to find an expression that captures the geometric meaning of the gradient, independent of the coordinate system used, which is a central theme in tensor calculus and vector calculus.

Mindmap

Keywords

💡Gradient

The gradient is a multifaceted concept in the script, primarily referring to the vector that points in the direction of the greatest rate of increase of a function, and its magnitude represents that rate of increase. It is a fundamental concept in vector calculus and differential geometry. In the video, the gradient is discussed in the context of two definitions: one geometric, which does not require coordinates, and another analytical, involving partial derivatives. The script explores the challenges of defining the gradient in various coordinate systems beyond Cartesian, emphasizing the need for an invariant definition.

💡Covariant Basis

A covariant basis is a set of vectors that are used to express other vectors in a given coordinate system. In the context of the video, the covariant basis is introduced as a means to generalize the concept of the gradient to non-Cartesian coordinate systems. The script discusses the necessity of defining a covariant basis to correctly express the gradient in arbitrary coordinate systems, such as polar or spherical coordinates.

💡Coordinate Basis

The coordinate basis refers to the set of unit vectors along the axes of a coordinate system, which are used to describe the position and direction in that system. In the script, the coordinate basis is contrasted with the covariant basis and is central to the discussion of how the gradient is represented in different coordinate systems. The transition from Cartesian to other coordinate systems is highlighted to show the need for a coordinate basis that can adapt to these changes.

💡Partial Derivatives

Partial derivatives are the rates at which a multivariable function changes with respect to one variable while holding the other variables constant. In the video, partial derivatives are initially presented as a way to define the gradient in Cartesian coordinates. However, the script also points out the limitations of this definition when applied to other coordinate systems, prompting a deeper exploration of the gradient's invariant properties.

💡Tensor Notation

Tensor notation is a mathematical notation used to express the components of tensors, which are generalizations of vectors and scalars to handle multiple dimensions and coordinate transformations. The script mentions the introduction of tensor notation as a tool for dealing with the complexities of expressing gradients in various coordinate systems, suggesting a move towards a more abstract and general notation that can accommodate different mathematical structures.

💡Directional Derivative

The directional derivative measures the rate of change of a function in a particular direction at a given point. In the video, the concept is used to explain how the gradient can be understood as the direction in which the function increases most rapidly. The script uses the directional derivative to connect the analytical expression of the gradient with its geometric interpretation.

💡Invariant

An invariant is a property or quantity that remains unchanged under certain transformations or in different coordinate systems. The script emphasizes the search for an invariant definition of the gradient that does not depend on the choice of coordinates, which is crucial for understanding the gradient's true geometric meaning.

💡Orthogonal Coordinate System

An orthogonal coordinate system is a coordinate system in which the coordinate lines intersect at right angles. The script discusses Cartesian coordinates as an example of an orthogonal system and then extends the discussion to include the challenges of defining the gradient in non-Cartesian orthogonal systems, such as polar coordinates.

💡Stretched Cartesian Coordinates

Stretched Cartesian coordinates refer to a modification of the standard Cartesian coordinate system where the unit lengths along the axes are scaled by different factors. In the script, this concept is used to illustrate the failure of the naive analytical expression for the gradient when applied to non-standard coordinate systems, highlighting the need for a more general definition.

💡Polar Coordinates

Polar coordinates are a two-dimensional coordinate system in which each point is determined by a radius from a fixed point and an angle from a fixed direction. The script mentions polar coordinates as an example of a coordinate system to which the definition of the gradient must be generalized, indicating the complexities involved in moving beyond Cartesian coordinates.

💡Dot Product

The dot product, also known as the scalar product, is an operation that takes two vectors and returns a scalar, which is the product of the magnitudes of the vectors and the cosine of the angle between them. In the video, the dot product is used to express the relationship between the gradient and the unit vector in the direction of interest, showing that the directional derivative is maximized when the gradient and the direction are aligned.

Highlights

Introduction to the concept of the gradient and its two definitions: the direction of greatest increase of a function and a pair of partial derivatives.

Discussion on the geometric interpretation of the gradient without the use of coordinates, using the analogy of temperature in a room.

Explaining the problem with defining the gradient in Cartesian coordinates and the need to move beyond them.

The quest to define the gradient in various coordinate systems, including the challenges with polar and spherical coordinates.

The attempt to connect the vector representation of the gradient with its partial derivative components in Cartesian coordinates.

Highlighting the importance of coordinate vectors and their role in defining the gradient.

The realization that the naive attempt to define the gradient in other coordinate systems fails, emphasizing the need for a more invariant definition.

Introduction of the concept of invariant expressions for the gradient that do not vary with coordinate systems.

The geometric versus analytical definitions of the gradient and the challenges in connecting the two.

Demonstration of how to find the gradient using the limit process by sampling points in the domain.

Discussion on the failure of the naive expression for the gradient in stretched Cartesian coordinate systems.

The normalization of the gradient vector to correct the failure in stretched coordinate systems.

The challenge of defining the gradient in polar coordinates and the need for an invariant expression.

The use of the directional derivative to understand the relationship between the gradient and the direction of greatest increase.

The remarkable formula that connects the directional derivative with the dot product of the gradient and a unit vector.

The proof that the direction of greatest increase corresponds to the gradient by using the dot product and the cosine of the angle between vectors.

The need to generalize the expression for the gradient to work in all coordinate systems, including affine and polar coordinates.

The importance of removing coordinate system artifacts to achieve a geometric meaning of the gradient.

The conclusion that an expression working in all coordinate systems has true geometric meaning due to its independence from specific coordinate artifacts.

Transcripts

Browse More Related Video

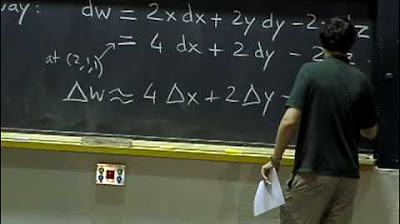
Lec 12: Gradient; directional derivative; tangent plane | MIT 18.02 Multivariable Calculus, Fall 07

Directional Derivatives (Calculus 3)

Calculus 3: Directional Derivatives and the Gradient Vector (Video #16) | Math with Professor V

Directional derivatives and slope

Directional Derivatives | What's the slope in any direction?

Why the gradient is the direction of steepest ascent

Related Tags

Gradient Mathematics Cartesian Coordinates Polar Coordinates Directional Derivative Vector Calculus Tensor Calculus Analytical Geometry Coordinate Systems Geometric Intuition