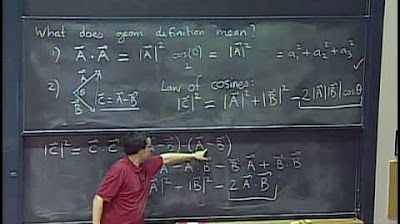Tensor Calculus 1: The Rules of the Game
TLDRThe video script delves into the fundamentals of tensor calculus, starting with the concept of Euclidean space as the basis for physical experience. It emphasizes the intuitive understanding of space, distance, and the importance of distinguishing vectors as directed segments, not merely numerical pairs. The script introduces the Cartesian coordinate system's significance and explores functions of space, such as temperature, and the vector's role in representing position. It also covers vector operations like addition, scalar multiplication, and the dot product, highlighting their geometric interpretations. The derivative of vectors, especially the position vector, is introduced, illustrating the application of limits in vector calculus.
Takeaways
- 📚 The script introduces tensor calculus with a focus on foundational concepts, beginning with 'The Rules of the Game' in Chapter 2.
- 🌐 It emphasizes the importance of understanding Euclidean space as the basis for physical experiences, where one can draw straight lines and measure distances.
- 📏 The script distinguishes Euclidean spaces from non-Euclidean spaces, such as the surface of a sphere, where straight lines cannot be drawn.
- 📐 The possibility of using a Cartesian coordinate system is highlighted as an important concept, even though it may not always be explicitly used.
- 📏 Distance is presented as a fundamental concept in Euclidean space, independent of coordinate systems, and is used to calculate areas and volumes.
- 🌡 The script mentions the concept of defining functions in space, such as temperature at different points in a room, without the need for a coordinate system.
- 🔍 The role of vectors, especially position vectors, is introduced as a fundamental concept derived from the ability to draw straight lines in Euclidean space.
- 📍 Vectors are described as directed segments, not merely pairs of numbers, and are the basis for operations like addition, subtraction, and scalar multiplication.
- 📈 The script explains the process of taking derivatives of vectors, especially the position vector, as a function of a parameter, which is a key operation in vector calculus.
- 🔄 The dot product of vectors is defined in terms of lengths and the angle between them, emphasizing its geometric interpretation rather than an algebraic operation.
- 🚀 The script concludes by discussing the application of limits to vectors, showing how the concept extends to these geometric objects and is essential for understanding derivatives.
Q & A
What is the primary concept discussed at the beginning of the script?
-The primary concept discussed at the beginning of the script is the concept of Euclidean space, which is the space of our common physical experience where we can draw straight lines, planes, and circles.
Why is the surface of a sphere not considered a Euclidean space?
-The surface of a sphere is not considered a Euclidean space because it does not allow for the drawing of straight lines, which is a fundamental aspect of Euclidean geometry.
What is the significance of being able to draw straight lines in Euclidean spaces?
-The ability to draw straight lines in Euclidean spaces is significant because it allows for the use of a Cartesian coordinate system, which is fundamental for various calculations and geometric constructions.
What is the role of distance in the context of the script?
-In the context of the script, distance is a fundamental concept that exists on its own terms. It is used to define units of measurement and to calculate areas and volumes of various shapes, including those with curved surfaces.
How does the script differentiate between scalar and vector functions?
-Scalar functions are defined as functions of space that assign a single value to each point, like temperature. Vector functions, on the other hand, assign a vector to each point in space, indicating both magnitude and direction.
What is the importance of the position vector in the script?
-The position vector is important because it represents the location of a point in space relative to an origin. It is a fundamental vector concept that is used to describe the position of points in Euclidean space.
Why does the script emphasize that vectors are not just pairs of numbers?
-The script emphasizes this to highlight that vectors should be understood as directed segments with both magnitude and direction, rather than merely as numerical representations, which is a common perspective in linear algebra.
What is the dot product of vectors as defined in the script?
-The dot product of vectors, as defined in the script, is the product of the lengths of the two vectors and the cosine of the angle between them, which is based on the primary concepts of length and angle in Euclidean space.
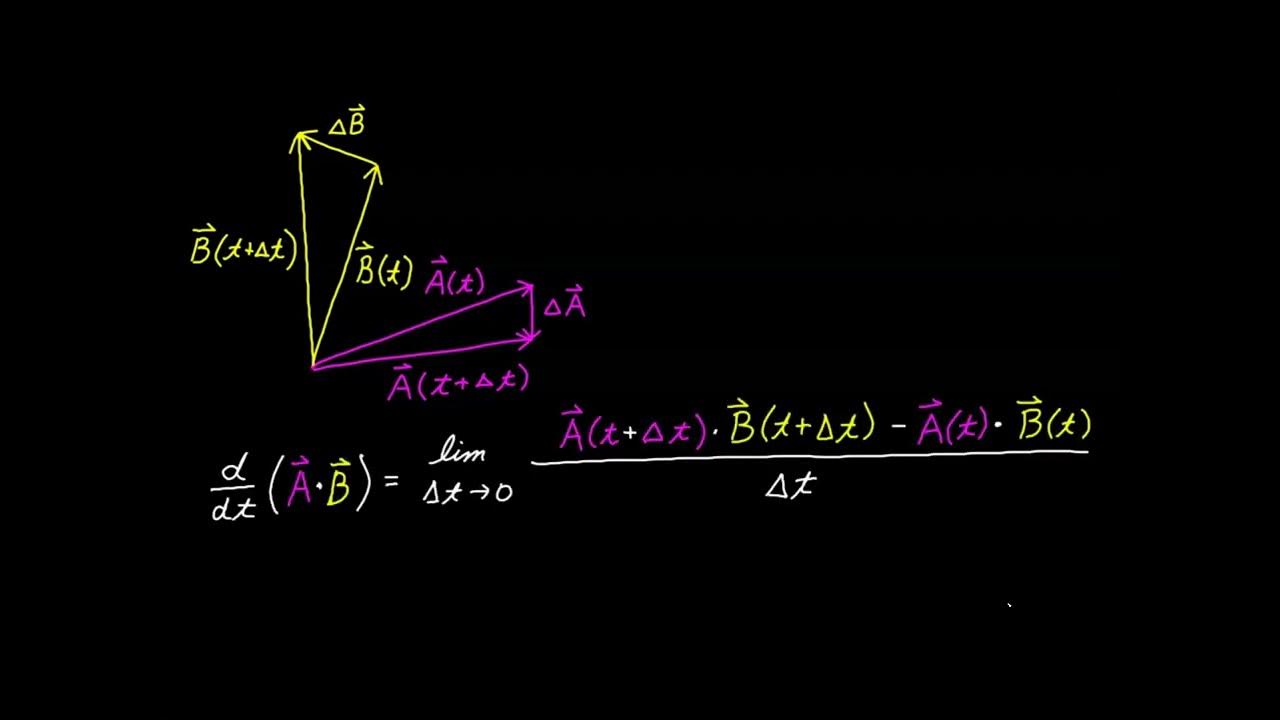
How does the script explain the concept of differentiating vectors?
-The script explains differentiating vectors by using the concept of limits, where the derivative of a vector function with respect to a parameter is the limit of the difference quotient as the parameter approaches zero.
What is the significance of the dot product in terms of a vector dotted with itself?
-When a vector is dotted with itself, the result is the square of its length. This property is significant as it provides a straightforward way to calculate the magnitude of a vector squared.
How does the script connect the concepts of length and angle to the operations on vectors?
-The script connects the concepts of length and angle to vector operations by using them as the basis for defining the dot product. It emphasizes that all operations on vectors should be understood in terms of these geometric concepts rather than purely algebraic representations.
Outlines
📚 Introduction to Tensor Calculus and Euclidean Space
The script begins an exploration of tensor calculus with a focus on foundational concepts. It introduces 'The Rules of the Game' as the starting chapter, emphasizing the need for a starting point in any discipline. The concept of space, specifically Euclidean space, is established as this fundamental starting point, characterized by the ability to draw straight lines, planes, and circles, and to measure distances. The script contrasts Euclidean space with non-Euclidean spaces, such as the surface of a sphere, which lacks straight lines. It also touches on the Cartesian coordinate system's importance and the intuitive understanding of distance, volume, and surface area, using examples like the volume of a sphere. The discussion on functions of space, such as temperature at different points, leads to the introduction of scalar functions and vectors, with an emphasis on the position vector as a fundamental vector concept.
🚀 Understanding Vectors and Vector Functions
This paragraph delves deeper into the nature of vectors, defining them as directed segments with both magnitude and direction, and contrasts this with the common but incorrect notion of vectors as mere pairs of numbers. The script stresses the importance of understanding vectors as geometric objects that can be added, multiplied by scalars, and even differentiated. It introduces the concept of a vector function, where each point in space is associated with a unique vector. The paragraph also explains that vectors are not decomposed into components with respect to a basis, as is common in linear algebra, but are to be accepted as standalone entities. The potential for vectors to represent changes, such as position changes over time, is introduced, setting the stage for the discussion of derivatives of vectors in the context of parameterized functions.
🔍 The Dot Product and Its Geometric Interpretation
The script introduces the dot product as a fundamental operation on vectors, emphasizing its definition in terms of the lengths of the vectors and the cosine of the angle between them. It contrasts this geometric interpretation with the algebraic approach often taught in linear algebra courses. The paragraph highlights the utility of the dot product, especially when used to find the square of a vector's length, and discusses its linearity, meaning that the dot product of a sum of vectors with another vector is the sum of the dot products of the individual vectors. The script reinforces the idea that the Euclidean space provides the necessary concepts of length and angle to define and work with the dot product, and it positions the dot product as a natural extension of these primary geometric notions.
🌐 Differentiating Vectors and Understanding Limits
The final paragraph of the script discusses the process of differentiating vectors, using the position vector as a prime example. It explains the concept of taking the derivative of a vector with respect to a parameter, illustrating it with a practical example involving a sequence of vectors approaching a specific vector as the parameter approaches a certain value. The script connects the idea of limits, traditionally associated with numerical sequences, to the geometric concept of vectors, emphasizing that the limit of a vector function can be visualized as one vector approaching another. The derivative is defined in the context of a small change in the parameter, leading to a discussion of the derivative as the limit of the ratio of the change in the vector to the change in the parameter, as the parameter approaches zero.
Mindmap
Keywords
💡Tensor Calculus
💡Euclidean Space
💡Distance
💡Surface Area
💡Vector
💡Position Vector
💡Vector-Valued Function
💡Dot Product
💡Differentiation
💡Limit
Highlights
Introduction to tensor calculus with an emphasis on the foundational concept of Euclidean space.
The importance of starting with intuitive concepts such as space and distance in Euclidean geometry.
Differentiating between Euclidean spaces and non-Euclidean spaces, such as the surface of a sphere.
The significance of Cartesian coordinate systems in the context of Euclidean spaces.
Understanding distance as a fundamental concept in Euclidean space, independent of coordinate systems.
The intuitive understanding of volume and surface area in Euclidean spaces without formal definitions.
Defining functions of space, such as temperature, without the need for a coordinate system.
The concept of scalar functions and their distinction from vector functions in space.
The introduction of vectors as fundamental quantities in Euclidean space, emphasizing their directed segment nature.
Clarification that vectors are not to be confused with pairs of numbers or decomposed into components.
The operation of vector addition and subtraction using geometric interpretations rather than algebraic.
The concept of derivatives of vectors and their application to position vectors.
The definition and importance of the dot product in vector calculus, relating to lengths and angles.
The geometric interpretation of the dot product as a product of lengths and cosine of the angle between vectors.
The linearity of the dot product and its properties in vector operations.
Differentiation of vectors as an extension of the concept of limits to vector quantities.
The geometric visualization of limits and derivatives applied to vectors, emphasizing the directed segment interpretation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: