MIT FINAL Exam Physics Problem

ZPhysics
27 Nov 202214:59
EducationalLearning
32 Likes 10 Comments

TLDRThis video script tackles a complex MIT final exam physics problem involving an Atwood machine with a fixed pulley, two blocks of mass m and 2m, and a string. The problem explores conditions for the blocks' motion on an inclined plane with friction and requires solving for acceleration using equations of motion and rotational mechanics. The script provides detailed steps to derive the conditions for upward or downward movement and the acceleration formula, offering a deep dive into the principles of physics.

Takeaways
  • 😲 The problem involves an Atwood machine with a fixed pulley wheel, a massless string, and two blocks of masses m and 2m.
  • 🔄 The lighter block is initially at a height D above the ground, while the heavier block is on an inclined plane with angle Alpha.
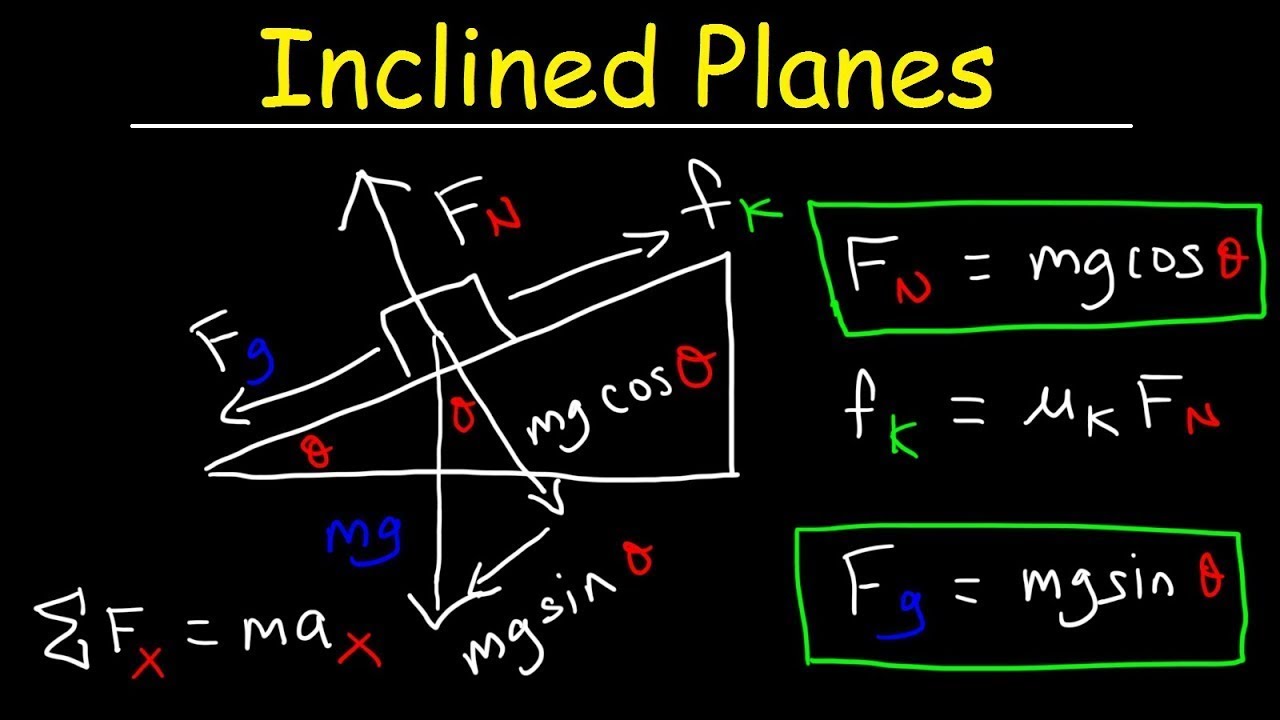
  • 🚫 There is friction between the block and the incline, with coefficient mu, and the string does not slip.
  • 📐 Part A of the problem requires determining conditions on Alpha for the block to move up or down.
  • 🔽 When the block is moving down, the weight of the 2m block must be greater than the tension T1, which in turn must be greater than T2.
  • 🔼 For the block to move up, the component of gravity along the slope must be greater than both the frictional force and T2.
  • 📈 The conditions for movement are derived from inequalities involving sine and cosine of Alpha, and the coefficient of friction.
  • 🧠 Part B of the problem is to find the acceleration of the system when the line block moves down.
  • 📚 Three equations of motion are written: one for each mass and one for the pulley, using principles of rotational mechanics.
  • 🔗 A key constraint is that all accelerations must be equal due to the string not slipping across the wheel.
  • 🔢 The acceleration is found by manipulating the equations to express tensions T1 and T2 in terms of the system's parameters.
  • 🎯 The final expression for acceleration involves gravitational acceleration, sine and cosine of Alpha, and the coefficient of friction.
Q & A

  • What is an Atwood machine?

    -An Atwood machine is a type of machine that consists of two masses connected by a string that passes over a pulley. It is used to study the dynamics of the system when the masses are allowed to move under the influence of gravity.

  • What are the conditions for the lighter block to move up or down in the Atwood machine described in the script?

    -For the lighter block to move down, the weight of the heavier block (mg) must be greater than the tension T1, which in turn must be greater than T2, and T2 must be greater than the component of gravity along the incline plus friction. For the block to move up, the component of gravity along the incline minus friction must be greater than T2, which must be greater than T1, and T1 must be greater than the weight of the lighter block (mg).

  • What is the mathematical condition for the block to move down?

    -The condition for the block to move down is that mg must be greater than 2mg sine(α) + μ(2mg) cosine(α). After simplification, this becomes sine(α) + μ cosine(α) < 1/2.

  • What is the mathematical condition for the block to move up?

    -The condition for the block to move up is that 2mg sine(α) - μ(2mg) cosine(α) must be greater than mg. After simplification, this becomes sine(α) - μ cosine(α) > 1/2.

  • What are the three equations of motion used to find the acceleration of the blocks in the Atwood machine?

    -The three equations of motion are: 1) For the leftmost block, mass times acceleration equals the net force (mg - T1). 2) For the pulley, the moment of inertia times angular acceleration equals the net torque (T1R - T2R). 3) For the 2m mass on the incline, 2m times acceleration equals T2 minus the gravitational component (2mg sine(α)) and the frictional component (μ(2mg) cosine(α)).

  • How is the moment of inertia of a cylinder calculated?

    -The moment of inertia of a cylinder about its central axis is given by (1/2)mr^2, where m is the mass and r is the radius of the cylinder.

  • What is the relationship between the accelerations of the blocks due to the no-slip condition?

    -Due to the no-slip condition, the accelerations of all blocks must be equal. This means that y'' (acceleration of the leftmost block) must equal Rθ'' (angular acceleration of the pulley), which must equal x'' (acceleration of the 2m block along the incline).

  • How is the tension T1 related to the other forces and tensions in the system?

    -T1 is related to the other forces and tensions by the equation 3T1 = mg + (2/3)T2. This equation is derived from the balance of forces acting on the blocks.

  • What is the expression for T2 in terms of the gravitational force, angle of inclination, and friction?

    -T2 can be expressed as T2 = (6/7)mg + (6/7)μ(2mg)cosine(α) + (6/7)(2mg)sine(α).

  • What is the final expression for the acceleration of the blocks in the Atwood machine?

    -The final expression for the acceleration of the blocks is y'' = g(2/7 - (4/7)sine(α) - (4/7)μcosine(α)).

  • How does the script relate the problem to the International Physics Olympiad?

    -The script suggests that solving this problem is akin to tackling a challenging problem for the International Physics Olympiad, indicating the complexity and depth of understanding required.

Outlines
00:00
🔍 Analyzing the Atwood Machine Problem

This paragraph introduces an MIT final exam physics problem involving an Atwood machine with a fixed pulley, two blocks of masses m and 2m, and a massless string. The problem explores the conditions for the heavier block to move up or down the incline. The conditions are derived from the forces acting on the blocks, including gravity, tension, and friction. The key is to find the angle Alpha for which the block can move in either direction, leading to two inequalities involving sine and cosine of Alpha, as well as the coefficient of friction.

05:02
📚 Calculating Acceleration in the Atwood Machine Scenario

The second paragraph delves into the acceleration of the Atwood machine system when the heavier block moves down. It starts by setting up three equations of motion for the two blocks and the pulley, incorporating rotational mechanics for the pulley's motion. The equations are then manipulated to express the tensions T1 and T2 in terms of the system's parameters. The paragraph concludes with a complex algebraic derivation that leads to expressions for T1 and T2, which are essential for finding the acceleration of the blocks.

10:06
🧩 Solving for Tensions and Acceleration in a Complex Physics Problem

The final paragraph continues the detailed mathematical analysis, aiming to express T2 in terms of the given angles and constants. It involves rearranging and solving a system of equations to isolate T2, then substituting this expression back into other equations to find T1. The process requires careful algebraic manipulation, including factoring and combining like terms. Ultimately, the paragraph derives an expression for the acceleration of the block, incorporating the gravitational force, the sine and cosine of the incline angle, and the coefficient of friction.

Mindmap
Keywords
💡Atwood Machine
An Atwood Machine is a type of simple machine that consists of two masses connected by a string over a pulley. It is used to study the principles of mechanics, particularly the balance of forces and acceleration. In the video, the Atwood Machine is central to the problem being solved, involving a fixed pulley wheel and two blocks of different masses.
💡Fixed Pulley
A fixed pulley is a wheel with a grooved rim that supports a rope or cable. It changes the direction of the force applied to the rope but does not provide a mechanical advantage. In the context of the video, the fixed pulley is part of the Atwood Machine and is crucial for the distribution of forces between the two masses.
💡Uniform Mass
Uniform mass refers to an object having a consistent density throughout, meaning its mass is evenly distributed. In the video, the pulley wheel is described as having a uniform mass, which simplifies the calculation of its moment of inertia in the rotational mechanics part of the problem.
💡Massless String
A massless string is an idealized concept where the string connecting the masses in the Atwood Machine has negligible mass. This simplification allows for the focus on the forces exerted by the masses themselves rather than the weight of the string, as seen in the script when calculating tensions T1 and T2.
💡Inclined Plane
An inclined plane is a simple machine that consists of a flat surface tilted at an angle, used to raise objects with less force than lifting them vertically. In the video, one of the blocks is positioned on an inclined plane, which introduces the component of gravity acting along the slope and the normal force perpendicular to it.
💡Coefficient of Friction
The coefficient of friction, denoted by mu in the script, is a dimensionless scalar value that represents the ratio of the force of friction between two bodies to the force pressing them together. It is a key factor in determining the conditions for motion in the Atwood Machine problem, as it affects the net force acting on the block on the inclined plane.
💡Tension
Tension, represented by T1 and T2 in the script, is the force transmitted through a string, rope, or wire when it is pulled tight by opposing forces. In the context of the Atwood Machine, tensions T1 and T2 are critical in the analysis of forces and accelerations of the two blocks.
💡Moment of Inertia
Moment of inertia is a measure of an object's resistance to changes in its rotation. For a uniform cylinder, like the pulley in the video, it is calculated as half the mass times the radius squared. It is essential in rotational mechanics and is used to relate the torque acting on the pulley to its angular acceleration.
💡Angular Acceleration
Angular acceleration is the rate of change of angular velocity with respect to time. In the video, it is used to describe the change in the rotational speed of the pulley wheel in the Atwood Machine as a result of the forces acting on it.
💡Acceleration
Acceleration is the rate of change of velocity of an object. In the script, the problem involves determining the acceleration of the blocks in the Atwood Machine as they move up or down, which is influenced by the tensions in the string, gravitational forces, and friction.
💡Equations of Motion
Equations of motion are mathematical equations that describe the relationship between the forces acting on an object and its motion. In the video, three equations of motion are written down to analyze the system: one for each mass in the Atwood Machine and one for the pulley wheel, considering both translational and rotational dynamics.
💡No-slip Condition
The no-slip condition is an assumption that the string does not slip on the pulley, which means that all parts of the string move at the same speed. This condition is crucial in the video as it allows the accelerations of the blocks to be related through the rotational motion of the pulley.
Highlights

An Atwood machine problem from an MIT final exam physics is being solved.

The problem involves a fixed pulley wheel of radius R and uniform mass m, with a massless string connecting two blocks of mass m and 2m.

The lighter block is positioned at a distance D above the ground, while the heavier block is on an inclined plane with an opening angle Alpha.

There is a coefficient of friction, mu, between the block and the incline plane, and the string never slips.

Two conditions on the angle Alpha are determined for the block to move up or down.

The weight of the 2m block must be greater than the tension T1, which in turn must be greater than T2 and the component of gravity along the decline plus friction.

A mathematical inequality is derived to express the conditions for the block to move down.

A second inequality is derived for the block to move up, with the component of gravity along the slope being greater than friction and T2.

Equations of motion are written for the leftmost block, the pulley, and the 2m mass on the inclined plane.

Rotational mechanics are applied to the pulley equation, considering the moment of inertia of a cylinder.

The accelerations of the blocks are constrained to be equal due to the string not slipping across the wheel.

An expression for T1 is derived in terms of T2, mg, and the mass of the blocks.

T2 is expressed in terms of the acceleration, gravitational component, frictional component, and angles Alpha.

The expression for T1 is further refined by substituting the derived expression for T2.

The acceleration of the block is found by substituting the expressions for T1 and T2 into the first equation.

The final expression for the acceleration includes factors of gravitational force, sine and cosine of Alpha, and the coefficient of friction.

The problem-solving approach is applicable to a challenging International Physics Olympiad problem.

Transcripts

Browse More Related Video

2019 #2 Free Response Question - AP Physics 1 - Exam Solution

Treating systems (the hard way) | Forces and Newton's laws of motion | Physics | Khan Academy

Incline Plane Problems with Friction

The Basic Atwood Machine With Friction

Introduction to Inclined Planes

2015 AP Physics 1 Free Response #1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Atwood MachinePhysics ProblemInequality ConditionsAcceleration CalculationInclined PlaneFriction AnalysisTension ForcesRotational MechanicsInternational OlympiadEducational ContentProblem Solving