2019 #2 Free Response Question - AP Physics 1 - Exam Solution

Flipping Physics

9 May 202011:20

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, the host guides students through solving a free response question from the 2019 AP Physics 1 exam. The problem involves two blocks with different masses on a frictionless table, connected by a string over a pulley. The video covers qualitative reasoning for acceleration scenarios, drawing free body diagrams, deriving an equation for acceleration in terms of masses and gravity, and comparing tensions with different pulley conditions. The host emphasizes the importance of understanding the physics behind the equations and provides insights into exam strategies.

Takeaways

📚 The video script is a discussion about solving a free response question from the 2019 AP Physics 1 exam.
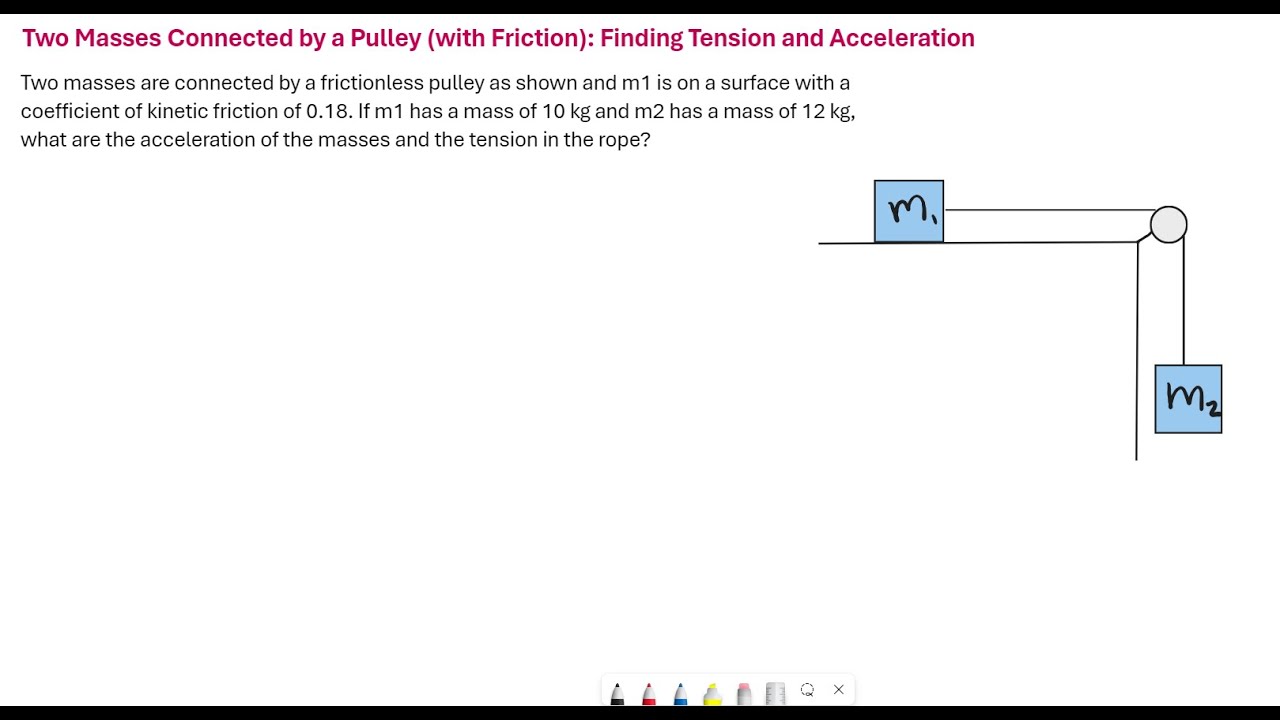
🔍 The problem involves two blocks with different masses, one on a table and the other hanging from a string over a pulley.
🧩 Part A of the problem asks to estimate acceleration given that one block is much heavier than the other, with an explanation required without using equations.
🏋️‍♂️ It is mentioned that a heavier block A would have nearly zero acceleration due to its large inertia resisting the tension from block B.
🪢 In Part A II, the scenario reverses, assuming block A is much lighter than block B, leading to an acceleration close to 9.81 m/s^2 for block A.
📈 Part B involves drawing free body diagrams for both blocks, labeling forces without breaking them into components.
📐 Part C requires deriving an equation for the acceleration of the blocks in terms of their masses and physical constants.
🔄 The solution to Part C uses the net force on both blocks and the principle that net force equals mass times acceleration.
🔄 The derived equation shows that acceleration is the gravitational force times the ratio of the mass of block B to the total mass of the system.
🔄 Part D confirms that the derived equation aligns with the qualitative reasoning from Part A II, especially when block A's mass is negligible.
🔧 Part II discusses the effect of replacing a negligible mass pulley with one of significant mass, resulting in a higher tension in the string due to decreased acceleration.
📝 The script emphasizes the importance of correctly labeling forces and understanding the physics behind the problem, not just the numerical answer.

Q & A

What is the primary concept explored in the problem discussed in the video?
-The problem explores how the relative masses of two blocks affect the acceleration of the blocks.
What is assumed about the mass of block A in Part A of the problem?
-It is assumed that the mass of block A is much greater than the mass of block B.
How does the mass of block A being much greater than the mass of block B affect the acceleration of the blocks?
-Block A has enough inertia to almost completely resist the tension force in the string, resulting in nearly zero acceleration for block A.
In Part A double I, what is the new assumption about the masses of the blocks?
-The new assumption is that the mass of block A is much less than the mass of block B.
What is the estimated magnitude of the acceleration of the blocks when the mass of block A is much less than the mass of block B?
-The magnitude of the acceleration of block A is nearly 9.81 m/s^2, which is the acceleration due to gravity.
What forces need to be drawn in the free body diagrams in Part B of the problem?
-For block A: force of gravity, force normal, and force of tension. For block B: force of gravity and force of tension.
What is the equation derived for the acceleration of the blocks in Part C?
-The acceleration of the blocks is given by (mass of Block B) / (mass of Block A + mass of Block B) * acceleration due to gravity.
Does the equation for acceleration in Part C agree with the reasoning in Part A double I?
-Yes, the equation agrees because when the mass of block A is much less than the mass of block B, the acceleration approaches 9.81 m/s^2.
How does the tension in the string change when a pulley with non-negligible mass is used instead of a pulley with negligible mass?
-The tension in the string increases because the new acceleration is smaller due to the increased resistance from the pulley's mass.
Why does the instructor write the tension force as F sub T?
-The instructor writes it this way to remind students that it is a force, helping them to remember the meaning of the variables.

Outlines

00:00

🔍 AP Physics 1 Free Response Question Analysis

This paragraph discusses the approach to solving a free response question from the 2019 AP Physics 1 exam. The scenario involves two blocks with different masses on a horizontal surface, connected by a light string and pulley system. The focus is on estimating the acceleration of the blocks when released from rest, given different mass ratios. The explanation emphasizes the qualitative reasoning behind the acceleration estimates without using equations, highlighting the inertia of the blocks and the tension force in the string.

05:01

📚 Deriving Acceleration Equation for Pulley System

In this section, the script explores different methods to derive an equation for the acceleration of the blocks after release, considering various force summations and conservation of energy principles. The chosen method involves summing the forces on both blocks in the direction of the string's tension, leading to a net force equation that equates to the combined mass times acceleration. The final equation for acceleration is expressed in terms of the masses of the blocks and the acceleration due to gravity, illustrating a clear understanding of the system's dynamics.

10:04

🔧 Impact of Pulley Mass on System Dynamics

This paragraph examines the effect of replacing a negligible mass pulley with one of significant mass on the tension in the string and the acceleration of the blocks. The analysis reveals that the introduction of a heavier pulley increases the system's resistance to velocity change, resulting in decreased acceleration and increased tension force. The explanation is grounded in the principles of force balance and the relationship between tension, mass, and acceleration, providing insight into how system components influence overall dynamics.

📝 Exam Strategy and Grading Insights

The final paragraph offers advice on exam strategy and grading, emphasizing the importance of answering all parts of every question for potential points. It also provides a specific example of how to correctly denote tension as a force variable (F_sub_T) to reinforce the concept of force identification. The paragraph concludes with a reminder of the value of each part of the question and the potential for partial credit based on sound physics reasoning, even if the final answer is incorrect.

Mindmap

Keywords

💡Acceleration

Acceleration is the rate of change of velocity of an object with respect to time. In the video, it is a central concept used to describe the motion of two blocks connected by a string over a pulley. The script discusses estimating the acceleration of the blocks and how it is affected by the relative masses of the blocks and the tension in the string.

💡Inertia

Inertia is the resistance of any physical object to any change in its state of motion or rest unless acted upon by an external force. The script refers to the inertia of block A to explain why, if it is much more massive than block B, it would resist the tension force in the string and result in a nearly zero acceleration.

💡Tension Force

Tension force is the force transmitted through a string or cable when it is pulled by exertions at opposite ends. In the context of the video, the tension force is what links the motion of block A and B and is central to the discussion of their acceleration. The script explores how changes in the system, such as adding mass to the pulley, affect this tension.

💡Free Fall

Free fall is the motion of an object when it is subject only to the force of gravity, without any other forces acting on it. The script mentions free fall in the context of block B's motion if block A were absent, which would result in an acceleration of 9.81 m/s², the acceleration due to gravity.

💡Friction

Friction is the force that resists the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. The script notes that there is negligible friction between block A and the tabletop, which simplifies the analysis by eliminating this force from the calculations.

💡Pulley System

A pulley system is a mechanism that uses one or more wheels (pulleys) to support and change the direction of applied forces. In the video, the pulley system is crucial as it allows block B to exert a force on block A, affecting their acceleration when released.

💡Mass

Mass is a measure of the amount of matter in an object. The script discusses the relative masses of two blocks, 'M sub a' and 'M sub B', and how these masses influence the system's dynamics, particularly their acceleration when connected by the string over the pulley.

💡Force Diagram

A force diagram is a visual representation of all the forces acting on an object. The script instructs to draw and label the forces on blocks A and B after release, which helps in understanding the physical situation and solving for acceleration.

💡Conservation of Energy

Conservation of energy is the principle that the total energy of an isolated system remains constant over time. The script suggests using conservation of energy to solve for the final velocities of the blocks and then using uniformly accelerated motion equations to find their acceleration.

💡Uniformly Accelerated Motion

Uniformly accelerated motion is motion in which an object's acceleration is constant. The script discusses the blocks' motion as uniformly accelerated, which allows for the use of specific equations to calculate their acceleration.

💡Newton's Second Law

Newton's second law of motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. Although not explicitly mentioned in the script, this law underlies the discussion of how the blocks' acceleration is calculated in terms of their masses and the forces acting on them.

Highlights

Introduction to solving free response question number two from the 2019 AP Physics 1 exam.

Exploration of how the relative masses of two blocks affect their acceleration.

Description of the setup with block A on a frictionless table and block B hanging from a string.

Qualitative translation question on the exam requiring reasoning without equations.

Estimation of block A's acceleration when its mass is much greater than block B's.

Explanation of inertia's role in resisting the tension force in the string.

Estimation of block A's acceleration being nearly zero due to its large mass.

Scenario where block A's mass is much less than block B's and its effect on acceleration.

Estimation of block A's acceleration being nearly 9.81 m/s^2 in the second scenario.

Drawing and labeling forces in free body diagrams for both blocks after release.

Instructions for not altering free body diagrams after initial drawing.

Derivation of an equation for the acceleration of the blocks in terms of their masses.

Use of net force and mass-times-acceleration to solve for acceleration.

Verification of the equation's agreement with the reasoning from part A.

Comparison of tensions in the string when a non-negligible mass pulley is introduced.

Explanation of how the addition of a heavier pulley affects the system's resistance and acceleration.

Conclusion on the increased tension force when acceleration decreases due to a heavier pulley.

Emphasis on the importance of answering every part of every question for potential points.

Transcripts

Browse More Related Video

2015 AP Physics 1 Free Response #1

2019 AP Physics 1 Solutions Free Response #2

Uniform Circular Motion Problems

Finding the Tension and Acceleration for a Two Mass Pulley (with Friction)

Newton's Second Law Exam Question: Two-body systems Pulley practice

2 Masses on a Pulley - Torque Demonstration