High School Physics - Parallel Plates and Equipotential Lines
TLDRThis script discusses the fundamentals of parallel plate capacitors and equipotential lines in the context of electric fields. It explains how to calculate the electric field strength between two charged plates and touches on the concept of potential difference. The script also delves into the relationship between Newtons per Coulomb and volts per meter, illustrating their equivalence through a mathematical explanation. Practical examples are given, such as sketching electric field lines and calculating the force on an electron within the field. The concept of equipotential lines as indicators of constant electrical potential is introduced, highlighting their perpendicular intersection with electric field lines. The information is presented in a clear and engaging manner to aid understanding of these key physics concepts.
Takeaways
- 📐 The formula to calculate the electric field strength between two parallel plates is E = V/d, where E is the electric field strength, V is the potential difference, and d is the separation between the plates.
- 🔋 The electric field strength is constant between the plates, except near the edges where there might be slight imperfections due to bending.
- 📈 The units for electric field strength calculated as E = V/d are volts per meter (V/m), which is equivalent to Newtons per Coulomb (N/C) when considering the force per unit charge.
- 🔧 To reconcile the units of Newtons per Coulomb and volts per meter, use the conversion that 1 N·m equals 1 Joule and 1 Joule per Coulomb equals 1 volt, thus 1 N/C = 1 V/m.
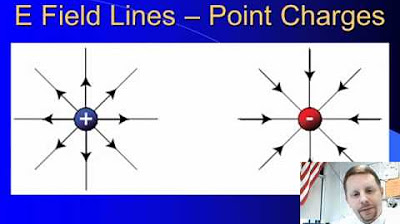
- 🖌️ When sketching electric field lines between two oppositely charged parallel plates, they should run from the positive to the negative plate, representing the direction of the force.
- 📍 For a point located midway between the plates, the electric field strength is given by E = V/d, where V is the potential difference and d is the distance between the plates.
- 🤖 The force exerted on an electron by the electric field can be calculated using the formula F = qE, where q is the charge of the electron and E is the electric field strength.
- 💡 If an electron is attracted to a particular plate, that plate must be positively charged, as opposite charges attract.
- 🌐 Equipotential lines represent areas of constant electrical potential, analogous to contour lines on a topographic map for gravitational potential.
- 🔲 Equipotential lines always cross electric field lines at right angles, indicating that moving along an equipotential line involves no change in potential energy.
- 📖 The force exerted by the electric field on two electrons with the same charge between parallel plates is the same, as it depends on the constant electric field strength and the charge of the electrons.
Q & A
What is the formula to calculate the electric field strength between two parallel plates?
-The electric field strength between two parallel plates can be calculated using the formula E = V/d, where E is the electric field strength, V is the potential difference between the plates, and d is their separation.
How does the electric field strength vary between the plates?
-The electric field strength is constant between the plates, driven by the potential difference divided by their separation. However, near the edges of the plates, the field can bend slightly, making it not perfectly uniform.
What are the units of electric field strength?
-The units of electric field strength are volts per meter (V/m) when calculated using the formula E = V/d.
How can we reconcile the units of electric field strength in Newtons per Coulomb with the units in volts per meter?
-We can prove that 1 Newton per Coulomb is the same as 1 volt per meter by multiplying 1 N/C by 1 meter/meter, which gives us 1 Newton meter/Coulomb meter. Since a Newton meter is a Joule, and 1 Joule per Coulomb is a volt, this simplifies to 1 volt per meter.
Given an electric field strength of 2×10^3 N/C, what is the force exerted on an electron located midway between two oppositely charged metal plates?
-The force exerted on the electron can be calculated using the formula F = qE, where q is the charge of the electron (-1.6×10^-19 C) and E is the electric field strength (2×10^3 N/C). So, F = (-1.6×10^-19 C) * (2×10^3 N/C) = -3.2×10^-16 N.
If an electron is attracted to plate A in the electric field between two parallel metal plates, what can we infer about the charge on plate A?
-If the electron is attracted to plate A, it means that plate A must be positively charged, as opposite charges attract.
What is the relationship between electric field lines and equipotential lines?
-Electric field lines and equipotential lines are perpendicular to each other. Electric field lines represent the direction of the electric force, running from positive to negative charges, while equipotential lines represent areas of constant electrical potential.
How do the forces exerted by the electric field on two electrons with the same charge compare if they are located in the same electric field?
-If two electrons are in the same electric field, the forces exerted on them by the electric field will be the same, as the electric force is proportional to the charge (which is the same for both electrons) and the electric field strength (which is constant in the region between the plates).
What is the significance of equipotential lines in the context of electric fields?
-Equipotential lines are significant because they represent lines of constant electrical potential. Charges moving along an equipotential line do not experience a force because the electric field is perpendicular to the direction of movement along the equipotential line, meaning no work is done by the electric field on the charge.
How do the electric field lines and equipotential lines relate to the distribution of charge in the parallel plates?
-The electric field lines radiate from the positively charged plate to the negatively charged plate, indicating the direction of the electric force. Equipotential lines, on the other hand, are perpendicular to the electric field lines and show the areas of constant potential. The distribution of charge on the plates creates a uniform electric field in the space between them, which is represented by parallel and equally spaced electric field lines.
What happens to the electric field strength at the edges of the parallel plates?
-At the edges of the parallel plates, the electric field strength is not perfectly uniform as it bends slightly due to the fringing effect. This results in a non-uniform electric field near the edges, which is different from the constant field strength in the bulk region between the plates.
How does the electric field strength affect the movement of charges within the field?
-The electric field strength determines the force experienced by charges within the field. A stronger electric field will exert a greater force on charges, leading to faster acceleration. In the case of the parallel plates, the constant electric field strength ensures that charges experience a consistent force, resulting in uniform acceleration if no other forces are acting on them.
Outlines
📚 Introduction to Parallel Plates and Electric Fields
This paragraph introduces the topic of parallel plates and equipotential lines in the context of electric fields. It sets the objective to solve basic problems involving charged parallel plates and explains how to calculate the electric field strength between two parallel plates using the formula E = V/d, where E is the electric field strength, V is the potential difference, and d is the separation between the plates. The paragraph also touches on the fact that the electric field is not perfectly uniform near the edges of the plates. It further discusses the units of electric field strength, explaining the equivalence of Newton per Coulomb and Volt per meter through a mathematical derivation. The application of these concepts is illustrated by calculating the force on an electron located midway between two oppositely charged metal plates.
🧲 Understanding Electric Fields and Equipotential Lines
This paragraph delves deeper into the concept of electric fields, particularly focusing on the representation of electric field lines and equipotential lines. It explains that electric field lines run from positive to negative charges and that equipotential lines, which represent constant electrical potential, always cross electric field lines at right angles. The analogy of equipotential lines to contour lines on a topographic map is used to illustrate this concept. The paragraph also discusses a scenario where an electron is attracted to one of the charged plates, deducing the charge on the plate based on the principle that opposite charges attract. Finally, it addresses a situation involving two electrons between charged parallel plates, comparing the forces exerted on them by the electric field, and concludes that the forces are the same due to the constant electric field strength and identical charges on the electrons.
Mindmap
Keywords
💡Parallel Plates
💡Equipotential Lines
💡Electric Field Strength
💡Potential Difference
💡Charge
💡Electric Force
💡Newton's Second Law
💡Coulomb's Law
💡Joule
💡Unit Conversion
💡Electric Potential
💡Right Angles
Highlights
The objective is to solve basic problems involving charge parallel plates in the electric field.
The electric field strength between two parallel plates is calculated using the formula E = V/d, where E is the electric field strength, V is the potential difference, and d is the separation between the plates.
The electric field strength is constant between the plates, except near the edges where things bend a little bit.
The units of electric field strength calculated using E = V/d is volts per meter (V/m).
Electric field strength is also expressed as Newton per Coulomb (N/C), which can be proven equivalent to volts per meter through a unit conversion process.
An example is given where the electric field strength between two oppositely charged metal plates is 2×10^3 N/C, and point P is located midway between the plates.
At least five electric field lines are to be sketched to represent the field between the oppositely charged plates.
The force exerted on an electron by the electric field is calculated using the formula F = qE, where F is the force, q is the charge, and E is the electric field strength.
If an electron is attracted to plate A, then plate A must be positively charged, and plate B must be negatively charged since opposites attract.
The electric field lines run from positive to negative, representing the direction of the force on a positive charge.
Equipotential lines are lines of constant electrical potential and always cross electric field lines at right angles.
In a topographic map analogy, equipotential lines are similar to lines showing areas of constant altitude or gravitational potential.
A positive charge is shown with electric field lines radiating away from it, and equipotential lines are depicted as circles crossing each electric field line at 90 degrees.
The force exerted by the electric field on two electrons between parallel plates is the same if the charges and the electric field strength are constant.
The practical applications of understanding parallel plates and equipotential lines are emphasized for solving problems in electric fields.
The transcript encourages seeking more help and looking for answers to questions at aplusphysics.com.
The importance of understanding the relationship between electric field strength, potential difference, and separation in parallel plate configurations is highlighted.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: