Physics - Optics: Refracted Surface (1 of 5) Swimming Pool
TLDRThis lecture delves into the principles of refracting surfaces in optics, explaining how light interacts with different media and curvatures to form images. It introduces the lens maker's equation to calculate image distance and magnification, using the example of a swimming pool to illustrate the concept. The lecture demonstrates how objects submerged in water appear closer and the same size due to refraction, providing a foundational understanding of optical phenomena.
Takeaways
- 🔍 The lecture discusses refracting surfaces in optics, where light interacts with a boundary between two media with different indices of refraction.
- 📚 The main equation used to find the image distance (s') involves the object distance (s), indices of refraction of the two media (n1 and n2), and the radius of curvature (R) of the boundary.
- 🌌 The magnification of the image is calculated using the formula involving the indices of refraction and the distances of the object and the image.
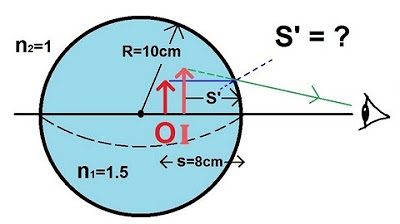
- 🏊♂️ An example of a swimming pool is used to illustrate the concept, where the object is at the bottom and the observer is looking from above.
- 🏞️ The index of refraction (n1) inside the pool is 1.33, and outside (n2) is 1, representing water and air respectively.
- 🔍 The radius of curvature is infinite for a flat boundary, simplifying the equation as division by infinity results in zero.
- 📏 The object distance in the pool example is 2 meters, which is used to calculate the image distance using the derived formula.
- 🔢 The calculated image distance (s') for the pool example is -1.5 meters, indicating a virtual image on the same side as the object.
- 🔄 The magnification in the pool scenario is 1, meaning objects appear the same size but closer to the observer due to the refraction.
- 🔄 The lecture will also cover examples with non-flat surfaces, where the boundary bulges towards or away from the observer, affecting the refraction and image formation.
- 📚 The principles learned can be applied to understand how lenses and mirrors work, as they are refractive surfaces with different indices of refraction.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is refracting surfaces in optics, which involves the behavior of light when it interacts with the boundary between two media with different indices of refraction.
What is the general equation used to find the image distance in the context of refracting surfaces?
-The general equation used to find the image distance (s') is given by \( \frac{n_1}{s} + \frac{n_2}{s'} = \frac{n_2 - n_1}{R} \), where \( n_1 \) and \( n_2 \) are the indices of refraction of the two media, \( s \) is the object distance, and \( R \) is the radius of curvature of the boundary.
How is the magnification of an image determined in the context of refracting surfaces?
-The magnification of an image is determined by the equation \( \text{Magnification} = -\frac{n_1 s'}{n_2 s} \), which takes into account the indices of refraction of the media and the distances of the object and the image from the refracting surface.
What does the sign of the radius of curvature indicate about the shape of the refracting surface?
-A positive radius of curvature indicates that the surface bulges away from the observer, while a negative radius of curvature indicates that the surface bulges towards the observer. A flat surface has an infinite radius of curvature.
In the swimming pool example, why is the radius of curvature considered to be infinite?
-In the swimming pool example, the radius of curvature is considered to be infinite because the boundary between the water and the air is flat, which means there is no curvature.
What is the significance of the negative image distance calculated in the swimming pool example?
-A negative image distance indicates that the image is formed on the same side as the object, which in this case means the image is a virtual image, not physically present but appearing to the observer.
Why do objects in a swimming pool appear the same size as they actually are?
-Objects in a swimming pool appear the same size because the magnification equation results in a value of 1, indicating no change in size between the object and its image.
What happens to the apparent distance of objects when viewed through a flat refracting surface like a swimming pool?
-The apparent distance of objects viewed through a flat refracting surface decreases, making the objects appear closer than they actually are.
How does the index of refraction affect the behavior of light at the boundary between two media?
-The index of refraction affects the speed and direction of light as it passes from one medium to another, which in turn influences the formation and properties of the image, such as its location and magnification.
What are some examples of refracting surfaces that are not flat?
-Examples of non-flat refracting surfaces include lenses and curved mirrors, which have different radii of curvature and can produce different types of images based on their shape and the indices of refraction of the media involved.
How can the principles discussed in the lecture be applied to understand the behavior of light in different optical systems?
-The principles discussed in the lecture can be applied to understand how light is refracted, reflected, and focused in various optical systems, such as lenses, mirrors, and prisms, by analyzing the indices of refraction and the curvature of the surfaces involved.
Outlines
🌟 Optics of Refracting Surfaces
This paragraph introduces the concept of refracting surfaces in optics, where light interacts with a boundary between two mediums with different indices of refraction. The lecture explains how objects can create images on the other side of the boundary, depending on the curvature of the boundary and the refractive indices of the mediums. The key formula for determining image distance (s') is presented, involving the object distance (s), the refractive indices (n1 and n2), and the radius of curvature (R) of the boundary. An example using a swimming pool illustrates the calculation of image distance and magnification, with the depth of the pool and the refractive index of water being key variables in the equation. The outcome shows a virtual image formed at a negative distance, indicating its position on the same side as the object, with the same size due to the magnification being equal to 1.
🔍 Magnification and Image Size in Refracting Surfaces
The second paragraph delves deeper into the implications of the refracting surfaces on the perceived size of objects. It uses the swimming pool example to demonstrate that objects under water appear the same size as they are, due to the magnification equation resulting in a value of 1. This signifies that there is no size distortion when viewing objects through a refracting surface, such as water. The paragraph also hints at further exploration of scenarios where the refracting surface is not flat, suggesting variations in the curvature towards or away from the observer, which will be addressed in subsequent examples to understand their impact on image formation.
Mindmap
Keywords
💡Refraction
💡Index of Refraction
💡Object Distance
💡Image Distance
💡Radius of Curvature
💡Lenses and Mirrors
💡Virtual Image
💡Magnification
💡Focal Length
💡Positive and Negative Curvature
💡Swimming Pool Example
Highlights
Introduction to the topic of refracting surfaces in optics where light interacts with a boundary between two mediums.
Explanation of how the index of refraction and the curvature of the boundary affect the formation of images.
The lensmaker's equation is introduced to calculate image distance given object position and medium properties.
Mention of the significance of the medium's index of refraction in determining the magnification of an image.
Clarification on the positioning of the observer, object, and the impact of the boundary's curvature on the perception of images.
Differentiation between positive and negative radius of curvature and their effects on image formation.
A practical example using a swimming pool to illustrate the principles of refraction and image formation.
Calculation of image distance using the lensmaker's equation with real-world values.
The concept that a flat boundary has an infinite radius of curvature simplifies certain calculations.
Determination of virtual image formation when the calculated image distance is negative.
Explanation of how the magnification equation shows that objects in water appear the same size but closer.
The practical application of understanding refraction in everyday scenarios like looking into a pool.
Introduction to further examples involving non-flat surfaces and their impact on refraction.
The importance of understanding different scenarios in optics for accurate image prediction.
Emphasis on the need to consider the medium's properties and boundary conditions in optical calculations.
The lecture's aim to provide a comprehensive understanding of refracting surfaces and their optical effects.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: