Thin lens equation and problem solving | Geometric optics | Physics | Khan Academy

khanacademymedicine
6 Jul 201412:56
EducationalLearning
32 Likes 10 Comments

TLDRThis educational script explains the thin lens formula and its sign conventions for focal lengths, object distances, and image distances. It clarifies that the focal length is positive for convex lenses and negative for concave lenses, while the object distance is always positive. The image distance's sign depends on its position relative to the object and the observer's perspective. The script also discusses the magnification formula, illustrating how positive and negative values indicate the orientation and size of the image formed by the lens.

Takeaways
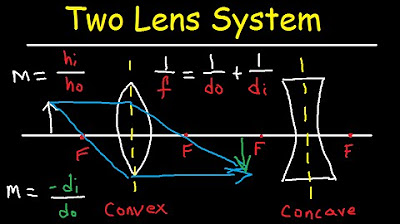
  • 🔍 The thin lens formula is given by 1/f = 1/do + 1/di.
  • 📏 The focal length (f) is positive for convex (converging) lenses and negative for concave (diverging) lenses.
  • 🔧 Object distance (do) is always positive for single lens systems.
  • 👁️ Image distance (di) is positive if the image is on the opposite side of the lens from the object and the same side as the observer's eye.
  • 🔄 Negative image distance indicates the image is on the same side as the object and opposite side of the observer's eye.
  • 📐 The magnification (M) is given by M = -di/do.
  • 🔄 Positive magnification indicates a right-side-up image, while negative magnification indicates an inverted image.
  • 📏 The thin lens formula only provides horizontal distances, not the height of the image or object.
  • 🔍 When solving for di, ensure to invert the final result after algebraic manipulation.
  • 🧮 The magnification formula can help determine the height and orientation of the image based on di and do.
Q & A

  • What is the thin lens formula and why is it used?

    -The thin lens formula is given by 1/f = 1/do + 1/di, where f is the focal length, do is the object distance, and di is the image distance. It is used to calculate the position and properties of the image formed by a thin lens.

  • How does the type of lens determine the sign of the focal length in the thin lens formula?

    -For a convex (converging) lens, the focal length is always positive. For a concave (diverging) lens, the focal length is always negative, regardless of the actual distances involved.

  • What is the significance of the focal point in the context of the thin lens formula?

    -The focal point is the point on each side of the lens where parallel rays of light converge or appear to diverge after passing through or around the lens. The focal length is the distance from the lens center to the focal point.

  • Is there a difference in how the focal length is measured for a convex lens compared to a concave lens?

    -No, the method of measuring the focal length is the same for both types of lenses. The difference lies in the sign of the focal length value used in calculations: positive for a convex lens and negative for a concave lens.

  • What is the rule for determining the sign of the object distance (do) in the thin lens formula?

    -The object distance (do) is always considered positive, regardless of the type of lens or the actual distance of the object from the lens.

  • Can the image distance (di) be negative, and if so, what does it indicate?

    -Yes, the image distance (di) can be negative. A negative image distance indicates that the image is formed on the same side of the lens as the object, which is typical for a virtual image formed by a diverging lens.

  • How is the image distance (di) measured in the context of the thin lens formula?

    -The image distance (di) is measured from the center of the lens to the location of the image, always parallel to the principal axis, regardless of whether the image is real or virtual.

  • What does the sign of the image distance tell us about the location of the image relative to the lens?

    -A positive image distance indicates that the image is on the opposite side of the lens from the object, while a negative image distance means the image is on the same side as the object.

  • How does the thin lens formula relate to the magnification of the image?

    -The thin lens formula does not directly provide information about the size or magnification of the image. Magnification is determined by the ratio of the image distance to the object distance, as given by the formula M = -di/do.

  • What does a positive magnification value indicate about the orientation of the image?

    -A positive magnification value indicates that the image is upright (not inverted) relative to the object.

  • What does a negative magnification value indicate about the orientation of the image?

    -A negative magnification value indicates that the image is inverted (upside down) relative to the object.

Outlines
00:00
🔍 Understanding Thin Lens Formula and Sign Conventions

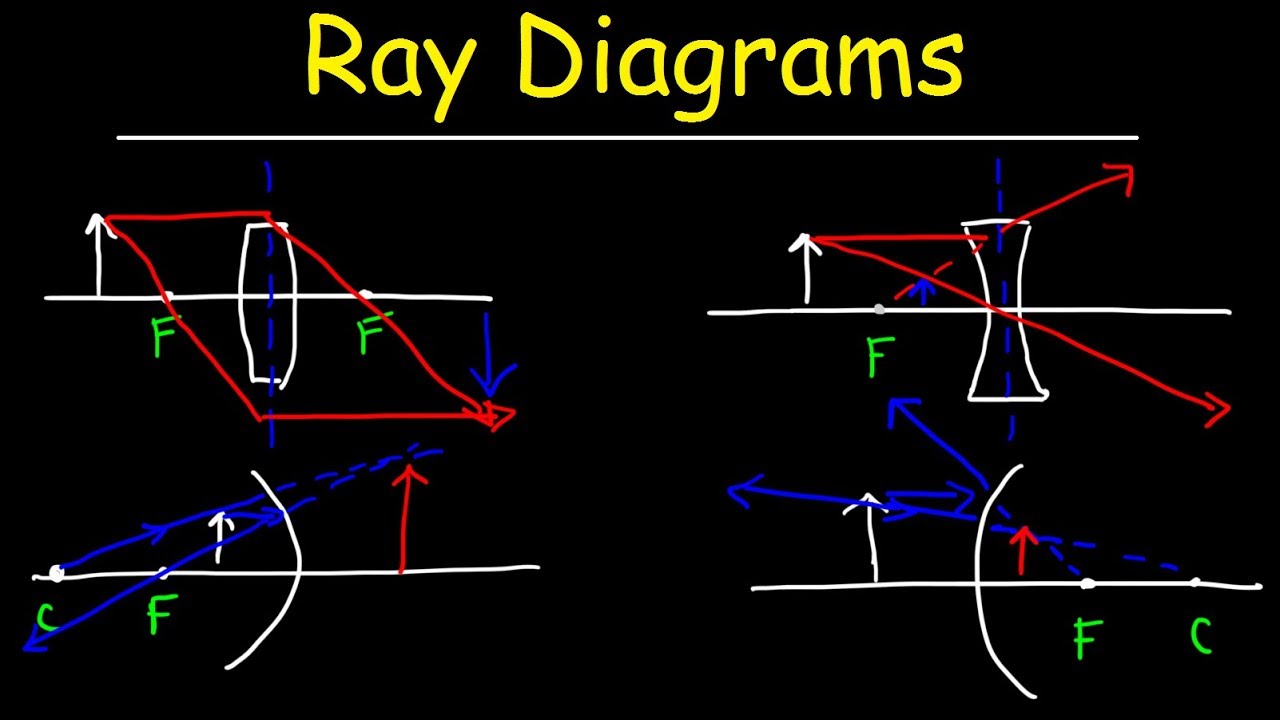
This paragraph explains the thin lens formula and how to determine the sign of focal lengths for both convex (converging) and concave (diverging) lenses. The focal length is always positive for a convex lens and negative for a concave lens. Object distance (d-o) is consistently positive, while image distance (d-i) can be positive or negative depending on the side of the lens relative to the object. The paragraph also clarifies that the formula only deals with horizontal distances and not the height of the image or object.

05:00
👀 Significance of Image Distance in Image Orientation

This section delves into the concept of image distance and its implications on the orientation of the image formed by a lens. It illustrates how a positive image distance indicates the image is on the same side as the observer's eye and the object, resulting in an upright image. Conversely, a negative image distance suggests the image is inverted and on the opposite side of the lens relative to the observer's eye. The explanation includes the use of the magnification formula to determine the size and orientation of the image.

10:03
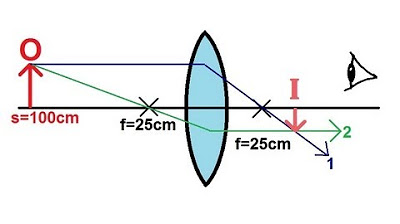
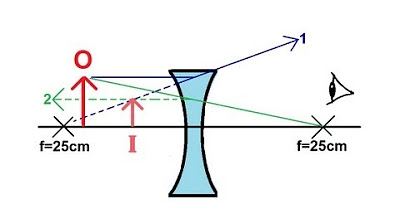
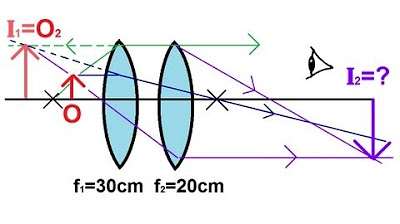
📐 Applying the Thin Lens Equation with an Example

The final paragraph provides a practical application of the thin lens equation using a given diagram and parameters. It demonstrates the process of calculating the image distance for a concave lens with a specific focal length and object distance. The solution shows that a negative image distance results in a right-side up image that is a fourth the size of the object, as determined by the magnification equation. This example solidifies the understanding of how to use the thin lens formula in various scenarios.

Mindmap
Keywords
💡Thin Lens Formula
The Thin Lens Formula is a fundamental equation in optics that relates the focal length of a lens to the distances of the object and the image from the lens. It is expressed as \( \frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i} \), where \( f \) is the focal length, \( d_o \) is the object distance, and \( d_i \) is the image distance. In the video, this formula is central to understanding how lenses form images and is used to calculate the position of the image formed by a lens.
💡Focal Length
Focal length is the distance from the center of a lens to its focal point, where parallel rays of light converge or appear to diverge. It is a key parameter in the Thin Lens Formula and is used to determine the nature of the lens, whether it is converging (convex) or diverging (concave). In the video, the focal length is described as always positive for convex lenses and negative for concave lenses.
💡Convex Lens
A convex lens, also known as a converging lens, bulges outward and is capable of focusing light rays to a single point, creating a real image. The video emphasizes that the focal length of a convex lens is always positive, which is crucial when applying the Thin Lens Formula.
💡Concave Lens
A concave lens is thinner in the middle than at the edges and causes light rays to spread out or diverge. It is used to form virtual images. The video script clarifies that the focal length of a concave lens is always negative, which is an important aspect when using the Thin Lens Formula.
💡Object Distance
Object distance refers to the distance from the center of the lens to the object being viewed. The video script explains that this distance is always positive, regardless of the type of lens, and is a necessary measurement for calculating image distance using the Thin Lens Formula.
💡Image Distance
Image distance is the distance from the center of the lens to the location where the image is formed. The video script explains that this distance can be positive or negative, depending on whether the image is formed on the same side or the opposite side of the lens relative to the object. Understanding image distance is essential for determining the position and orientation of the image.
💡Magnification
Magnification is the ratio of the image size to the object size and is a measure of how much an image is enlarged or reduced by a lens. The video script introduces a formula for magnification, \( M = -\frac{d_i}{d_o} \), which is used to determine whether the image is upright or inverted and its relative size compared to the object.
💡Positive Image Distance
A positive image distance indicates that the image is formed on the same side of the lens as the observer's eye when looking through the lens at the object. The video script uses this concept to explain that a positive image distance results in an inverted image, as the image is on the opposite side of the lens from the object.
💡Negative Image Distance
A negative image distance means the image is formed on the opposite side of the lens from the observer's eye, relative to the object. The video script explains that a negative image distance results in an upright image, as the image is on the same side of the lens as the object.
💡Principal Axis
The principal axis is an imaginary line that passes through the center of a lens and is perpendicular to its faces. It serves as a reference for measuring distances in lens equations. The video script mentions that all distances, whether for object or image, are measured parallel to the principal axis.
💡Real Image
A real image is formed when light rays actually converge at a point and can be projected onto a screen. The video script discusses real images in the context of convex lenses, which can form real images on the opposite side of the lens from the object.
💡Virtual Image
A virtual image is formed when light rays appear to diverge from a point; it cannot be projected onto a screen but can be seen by looking through the lens. The video script mentions virtual images in the context of concave lenses, which form virtual images on the same side as the object.
Highlights

The thin lens formula 1/f = 1/do + 1/di is used for calculating the focal length and distances in lens systems.

Focal length (f) is always positive for convex lenses and negative for concave lenses, regardless of the side of measurement.

The type of lens dictates the sign of the focal length, with convex lenses having a positive focal length and concave lenses a negative one.

Object distance (do) is always positive, as it is measured from the lens to the object.

Image distance (di) can be positive or negative depending on whether the image is on the same or opposite side of the lens relative to the object.

A positive image distance indicates the image is on the opposite side of the lens as the object, and the observer's eye should be on the same side as the image.

A negative image distance means the image is formed on the same side as the object, which is useful for understanding virtual images.

The thin lens formula only provides horizontal distances and does not account for the height of the image or object.

Magnification is calculated using the formula M = -di/do, where a positive magnification indicates an upright image.

A negative magnification results in an inverted image, which is crucial for understanding the orientation of the image formed by the lens.

The sign conventions for the thin lens formula are essential for correctly calculating image properties in optical systems.

An example is provided to demonstrate the application of the thin lens formula and magnification equation in determining image distance and orientation.

In the example, a concave lens with a focal length of -8 cm and an object distance of 24 cm is used to find the image distance.

The solution to the example yields an image distance of -6 cm, indicating a right-side up, reduced-size virtual image.

The magnification equation confirms the image is right-side up and one-fourth the size of the object.

The process of solving the example illustrates the practical application of the thin lens formula in optical calculations.

Transcripts

Browse More Related Video

Multiple Two Lens System with Diverging and Converging Lens

Physics - Optics: Lenses (1 of 4) Converging Lens

Physics - Optics: Lenses (2 of 2) Diverging Lens

Ray Diagrams

GCSE Physics - How to Draw Ray Diagrams #70

Physics - Optics: Lenses (2 of 5) Lens Combinations - Two Converging Lenses

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Thin LensOpticsFocal LengthConverging LensDiverging LensImage DistanceObject DistanceMagnificationPhysics EducationConcept Explanation