Unit VII: Lec 2 | MIT Calculus Revisited: Single Variable Calculus
TLDRThe video script from an MIT OpenCourseWare lecture introduces the concept of 'Positive Series,' focusing on series where every term is non-negative. It discusses preliminary topics such as ordering sets, defining upper and lower bounds, and the properties of monotonic non-decreasing sequences. The lecturer then presents three tests for convergence: the comparison test, the ratio test, and the integral test, providing geometric interpretations and proofs for each. The goal is to determine whether a positive series converges to a limit or diverges to infinity, with the integral test linking series to improper integrals for comparison.
Takeaways
- 📚 The lecture discusses the concept of 'Positive Series' and their significance in mathematical analysis.
- 🔢 It introduces the process of ordering finite sets and the concept of upper and lower bounds, with examples to illustrate these concepts.
- 📉 The professor explains the difference between finite and infinite sets, particularly how the latter can have bounds that are not members of the set itself.
- 🔑 Key definitions are provided, such as upper bound, lower bound, least upper bound (LUB), and greatest lower bound (GLB).
- 📈 The importance of monotonic non-decreasing sequences is discussed, along with the properties that such sequences either diverge to infinity or converge to a limit.
- 🌟 A bounded set of numbers always has both a greatest lower bound and a least upper bound, which is a fundamental property in understanding series.
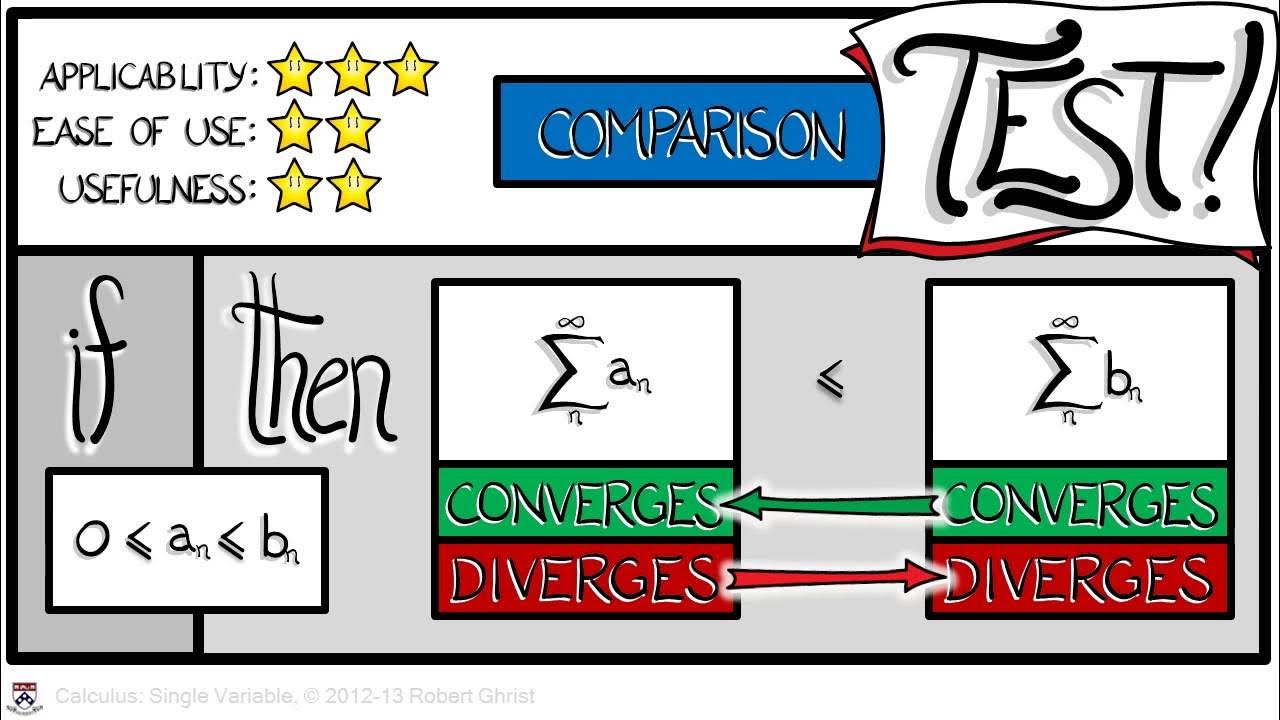
- 📊 The lecture introduces three major tests for the convergence of positive series: the comparison test, the ratio test, and the integral test.
- 📚 The comparison test is explained with examples, highlighting how it can be used to determine the convergence of a series by comparing it with a known convergent or divergent series.
- 📐 The ratio test is introduced, showing how the limit of the ratio of consecutive terms can indicate whether a series converges or diverges.
- 📘 The integral test is presented as a method to compare a positive series with an improper integral, where both converge or diverge together.
- 🔍 The professor emphasizes the practical application of these tests, noting that while they are powerful, they may not always be straightforward to apply without prior knowledge of the series' behavior.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is 'Positive Series', which refers to series where every term is non-negative.
Why is the process of ordering important in the context of this lecture?
-The process of ordering is important as it helps in understanding the concepts of upper and lower bounds, which are fundamental when dealing with infinite sets and series.
What is the difference between an upper bound and a least upper bound (LUB) for a set?
-An upper bound for a set is any number that is greater than or equal to all the elements in the set. A least upper bound (LUB), however, is the smallest number that can be an upper bound for the set.
Can the least upper bound of a set be a member of the set itself?
-No, the least upper bound of a set does not have to be a member of the set itself, as illustrated by the example where the set 'S' consists of numbers 'n' over 'n + 1', where the LUB is 1 but 1 is not a member of 'S'.
What is a monotonic non-decreasing sequence?
-A monotonic non-decreasing sequence is a sequence where each term is greater than or equal to the term that came before it, meaning no term can be smaller than its predecessor.
What are the two possible outcomes for a monotonic non-decreasing sequence that is bounded?
-For a bounded monotonic non-decreasing sequence, the two possible outcomes are that it either diverges to infinity, or it converges to a limit, which is the least upper bound of the sequence.
What is the comparison test for series convergence?
-The comparison test states that if you have a known convergent positive series and another series where each term of the second series is less than or equal to the corresponding term of the first series, then the second series must also converge.
What is the ratio test for series convergence?
-The ratio test involves forming a sequence of ratios between consecutive terms of a series. If the limit of this sequence, denoted as 'rho', is less than 1, the series converges; if 'rho' is greater than 1, the series diverges; and if 'rho' equals 1, the test is inconclusive.
What is the integral test for series convergence?
-The integral test equates a positive series with an improper integral of a decreasing continuous function. If the integral converges, then so does the series, and if the integral diverges, the series does as well.
What is the significance of the integral test in relation to the comparison test?
-The integral test is a companion to the comparison test as it provides another method to determine the convergence of a series by comparing it to the convergence of an improper integral, which can be easier to evaluate in some cases.
Outlines
📚 Introduction to Positive Series and Ordering
The video begins with a male speaker discussing the support for MIT OpenCourseWare and transitions to a professor introducing the topic of 'Positive Series'. The professor explains the preliminary concept of ordering numbers in a set, using an example set 'S' with the numbers 11, 8, 9, 7, and 10. A binary technique is described to find the least member of the set, which is identified as the lower bound, with 7 being the greatest lower bound (GLB) and 11 the least upper bound (LUB) for 'S'. The lecture then contrasts the simplicity of ordering finite sets with the complexities that arise with infinite sets, using the set 'S' with terms 'n/(n+1)' as an example where the LUB is 1, which is not a member of 'S'.
🔢 Understanding Upper and Lower Bounds in Infinite Sets
The second paragraph delves deeper into the concept of upper and lower bounds, especially in the context of infinite sets. The professor provides definitions for upper bounds, least upper bounds (LUB), lower bounds, and greatest lower bounds (GLB). It is established that every bounded set has both a LUB and a GLB, a principle that is pivotal for understanding infinite sets. The paragraph also introduces the concept of a bounded set and the significance of the LUB and GLB not necessarily being members of the set itself, using the examples of the sets 'S' with terms '1/n' and 'n/(n+1)' to illustrate these points.
📈 Monotonic Non-Decreasing Sequences and Their Limits
The third paragraph discusses monotonic non-decreasing sequences, where each term is greater than or equal to the one preceding it. The professor explains that such sequences can either have no upper bound and diverge to infinity or be bounded and converge to a limit, which is the LUB of the sequence. A geometric proof is given to demonstrate that if a monotonic non-decreasing sequence is bounded, its limit exists and is equal to the LUB. The importance of this concept is highlighted in the context of understanding the behavior of sequences and their limits.
📊 The Importance of Monotonic Sequences in Series Convergence
In the fourth paragraph, the professor connects the concept of monotonic non-decreasing sequences to the convergence of series. It is explained that the sequence of partial sums of a series is monotonic non-decreasing if each term of the series is non-negative. The paragraph introduces the idea that a positive series, which is a series with non-negative terms, either diverges to infinity or converges to a limit, which is the LUB of the sequence of partial sums. The professor also mentions that the next part of the lecture will cover tests for determining the convergence of positive series.
📝 The Comparison Test for Series Convergence
The fifth paragraph introduces the comparison test, a method for determining the convergence of a positive series by comparing it with another known series. If a series is term-by-term less than or equal to a known convergent series, then it must also converge. The professor illustrates this with examples and explains the conditions under which the comparison test can be applied. It is noted that while the comparison test is theoretically sound, it may not always be practical if a suitable series for comparison is not readily known.
📚 The Ratio Test and Its Implications for Series Convergence
The sixth paragraph presents the ratio test, another tool for assessing the convergence of a series. The ratio test involves forming a sequence from the ratios of successive terms of the series and examining the limit of this sequence as it approaches infinity. If this limit, denoted as 'rho', is less than 1, the series converges; if 'rho' is greater than 1, the series diverges; and if 'rho' equals 1, the test is inconclusive. The professor provides an example to illustrate the application of the ratio test and emphasizes the difference between the limit of the ratio sequence and the individual terms being less than 1.
📘 The Integral Test and Its Relation to Series Convergence
The seventh and final paragraph of the provided script discusses the integral test, which allows for the comparison of a positive series with an improper integral. The test states that if there is a continuous, decreasing function 'f(x)' such that 'f(n)' equals the n-th term of the series, then the convergence of the series is equivalent to the convergence of the integral from 1 to infinity of 'f(x)' with respect to 'x'. The professor explains this concept with a visual representation, showing how the areas under the curve can be compared to the sum of the series terms to determine convergence. The integral test is highlighted as a powerful method for testing series convergence, especially when combined with the comparison test.
Mindmap
Keywords
💡Creative Commons license
💡Positive Series
💡Ordering
💡Lower Bound and Upper Bound
💡Greatest Lower Bound (GLB)
💡Least Upper Bound (LUB)
💡Monotonic Non-Decreasing Sequence
💡Convergence
💡Comparison Test
💡Ratio Test
Highlights
Introduction to the concept of 'Positive Series' where every term in the series is positive.
Explanation of ordering and the process of finding the least and greatest elements in a set.
Binary technique for ordering elements of a set based on size.
Definition and significance of lower and upper bounds in a set.
Concept of greatest lower bound (GLB) and least upper bound (LUB).
Difference between finite and infinite sets in terms of upper and lower bounds.
Example of a set where the LUB is not a member of the set itself.
Introduction to the definition of an upper bound and its properties.
Explanation of a least upper bound and its relationship to a bounded set.
Definition and importance of a monotonic non-decreasing sequence.
Behavior of monotonic non-decreasing sequences and their limits.
Geometric proof illustrating the limit of a monotonic non-decreasing sequence.
Introduction to the main topic of positive series and their properties.
Description of how the sequence of partial sums relates to the convergence of a series.
Overview of the comparison test for determining the convergence of a series.
Explanation of the ratio test and its application to positive series.
Illustration of the integral test and its use in comparing series with improper integrals.
Fundamental theorems and properties discussed for understanding convergence in positive series.
Conclusion and preview of the next lecture's focus on series that are not positive.
Transcripts
Browse More Related Video
Calculus Chapter 5 Lecture 51 Convergence Tests 1

Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test

A Lot of Series Test Practice Problems

Series Tests - Limit Comparison Test

Calculus 2 Lecture 9.3: Using the Integral Test for Convergence/Divergence of Series, P-Series
Estimating Sums Using the Integral Test and Comparison Test
5.0 / 5 (0 votes)
Thanks for rating: