Unit II: Lec 8 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis MIT lecture explores the concepts of maxima and minima from both analytical and geometric perspectives. Professor Herbert Gross introduces the fundamental theorem for identifying local maxima and minima, emphasizing the importance of the derivative at a point. He cautions against misinterpreting the theorem and illustrates the difference between local and absolute extrema. The lecture also highlights the practical applications of these concepts, such as optimizing the volume of a cylinder under a given constraint, and demonstrates the balance between intuitive and rigorous calculus.
Takeaways
- 📚 The lecture introduces the concept of maxima and minima, also known as high and low points, within the context of calculus.
- 🔍 The fundamental theorem for studying maxima and minima is presented, which states that if 'f of c' is at least as great as 'f of x' for all 'x' in a delta neighborhood of 'c', and 'f prime of c' exists, then 'f prime of c' must be 0.
- 📈 The geometric interpretation of the theorem is explained, illustrating that a positive derivative indicates a rising curve, which cannot represent a maximum within a neighborhood.
- 📉 Similarly, if 'f of c' is less than or equal to 'f of x' in a neighborhood, and the derivative exists, it cannot be a minimum.
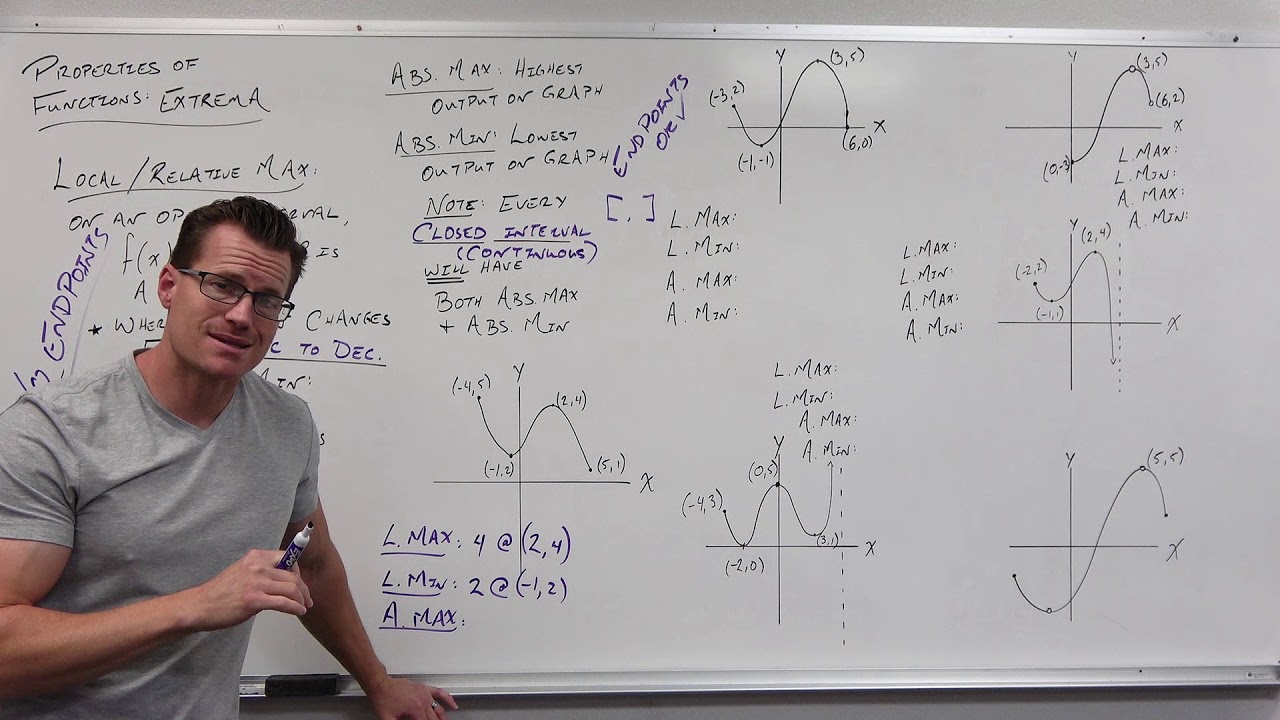
- 👀 The importance of considering 'local' or 'relative' maxima and minima in addition to 'absolute' ones is highlighted, emphasizing the relevance of the domain in practical applications.
- ⚠️ The lecture warns against false converses, where the inverse of a true statement may not hold true, using the example of a person being alive to listen to a lecture, but not every living person listening to the lecture.
- 🈚️ It is cautioned that the existence of 'f prime of c' being 0 does not guarantee a local maximum or minimum, and an example is given where 'f prime of c' is 0 but no extremum exists in the neighborhood.
- 🚫 The potential issue of 'f prime of c' not existing at certain points is discussed, with an example of the absolute value function, where the derivative does not exist at x=0, yet it is a minimum.
- 📐 The difference between open and closed intervals is explored, showing that a continuous function on a closed interval must have its maximum and minimum values at the endpoints or within the interval.
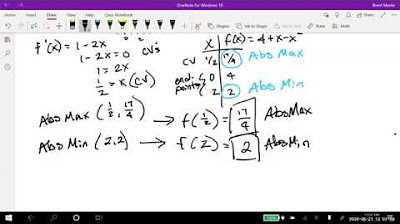
- 📏 An example of a cylinder optimization problem is presented, demonstrating how to apply calculus to find the dimensions that maximize volume under a given constraint.
- 📉 The relationship between the area of a rectangle and the volume of a cylinder formed by revolving the rectangle is discussed, illustrating the non-linear relationship between dimensions and volume.
Q & A
What is the fundamental theorem for the study of maxima and minima as described in the lecture?
-The fundamental theorem states that if 'f of c' is at least as great as 'f of x' for all 'x' in a delta neighborhood of 'c', and 'f prime of c' exists, then 'f prime of c' must be 0. This implies that at a local maximum or minimum where the derivative exists, the derivative is zero.
Why is it important to consider the domain of a function when finding maxima and minima?
-The domain of a function restricts the set of input values that the function can take. When finding maxima and minima, it is important because the highest or lowest points might occur at the boundaries of the domain, especially if the function is continuous on a closed interval.
What is the difference between a local maximum or minimum and an absolute maximum or minimum?
-A local maximum or minimum refers to a point where the function value is higher or lower than all nearby points within a small neighborhood, but not necessarily the highest or lowest value the function can take. An absolute maximum or minimum is the highest or lowest value the function can take over its entire domain.
Why should one be cautious about the converse of the fundamental theorem for maxima and minima?
-One should be cautious because the converse of the theorem, which would state that if 'f prime of c' is 0 then there is a local maximum or minimum, is not necessarily true. A zero derivative does not guarantee a maximum or minimum due to potential exceptions such as points where the derivative does not exist or the function behavior at endpoints.
What is an example of a function where the derivative does not exist at a point, yet it is a minimum?
-An example given in the lecture is the function 'f of x' equal to the absolute value of 'x'. The derivative does not exist at 'x' equals 0, but this point is an absolute minimum because the function changes from decreasing to increasing, creating a 'V' shape with the lowest point at the vertex.
Why is it incorrect to assume that a point where the derivative is zero must be a maximum or minimum?
-It is incorrect because the derivative being zero only indicates a potential candidate for a maximum or minimum. However, without further analysis, such as checking the second derivative or the behavior of the function around that point, one cannot conclude it is indeed a maximum or minimum.
What is the significance of the open interval in the context of the lecture?
-The open interval is significant because it defines the neighborhood around a point where the function's behavior is analyzed for maxima and minima. The open interval excludes the endpoints, which means that when looking for maxima and minima, one must consider the endpoints separately if the interval is closed.
How does the lecture illustrate the difference between an open and a closed interval in terms of function maxima and minima?
-The lecture uses the example of the function 'f of x' equals 'x squared' with different domains. On an open interval from 2 to 3, there are no maxima or minima because the derivative is never zero and the function is continuous without endpoints. On a closed interval from 2 to 3, the endpoints must be checked, and it turns out that the minimum is at 'x' equals 2 and the maximum is at 'x' equals 3.
What is the practical implication of the lecture's discussion on the volume of a cylinder given a fixed sum of radius and height?
-The practical implication is that if you have a constraint on the total height and radius of a cylinder and you want to maximize the volume, you should choose the dimensions where the derivative of the volume function with respect to one of the variables is zero, given the constraint. In the lecture's example, the optimal dimensions are when the radius is 20 and the height is 10.
How does the lecture demonstrate the relationship between the analytical and geometric interpretations of maxima and minima?
-The lecture demonstrates this relationship by first explaining the analytical definition of maxima and minima in terms of derivatives and then illustrating the geometric interpretation with curves and tangents. It shows how the geometric visualization can motivate the analytical proof and vice versa.
Outlines
📚 Introduction to Maxima and Minima
The first paragraph introduces the topic of the lecture, which is the study of maxima and minima, or high and low points, in the context of both analytical and geometric perspectives. The fundamental theorem for analyzing these points is presented, which states that if 'f of c' is at least as great as 'f of x' for all 'x' in a delta neighborhood of 'c', and if 'f prime of c' exists, then 'f prime of c' must be zero. The geometric interpretation is also discussed, illustrating how the derivative's sign can indicate whether a point is a maximum or minimum by showing that a positive derivative indicates an increasing function, and thus cannot be a maximum within a neighborhood.
🔍 Understanding Local vs. Absolute Extrema
The second paragraph delves into the concepts of local and absolute maxima and minima, explaining the difference between them and how constraints can affect which points are considered high or low. The importance of the domain of a function in practical applications is highlighted, and the potential confusion between global and local extrema is addressed. The paragraph also warns against misinterpreting the fundamental theorem by presenting 'three commandments' to avoid common mistakes, such as assuming the converse of the theorem is true or overlooking points where the derivative does not exist.
🚫 Cautionary Tales on Derivatives and Extrema
In the third paragraph, the lecturer emphasizes the importance of being cautious with the conclusions drawn from the fundamental theorem. It is cautioned that a point where the derivative is zero does not necessarily indicate a maximum or minimum, and vice versa, a maximum or minimum does not guarantee that the derivative at that point is zero. Examples are provided to illustrate these points, including a case where the derivative does not exist at a minimum point, and another where the derivative does not exist without indicating a maximum or minimum.
🏛 The Significance of Open and Closed Intervals
The fourth paragraph discusses the difference between open and closed intervals in the context of finding extrema. It explains that while a continuous function on a closed interval must attain its maximum and minimum values somewhere on that interval, the situation is different for open intervals. The importance of checking endpoints in closed intervals is highlighted, using the example of a function defined on the closed interval from 2 to 3, where the function 'f of x' equals 'x squared', and it is shown that the maximum and minimum values occur at the endpoints.
📉 Analyzing the Behavior of Functions at Endpoints
The fifth paragraph continues the discussion on the behavior of functions at endpoints, especially in the context of closed intervals. It explains that while the endpoints of a closed interval may not necessarily represent absolute high or low points, they must be considered as potential candidates for maxima or minima if the function is continuous over that interval. The paragraph also provides an example of a function where the endpoints do not represent the absolute extrema, reinforcing the need to analyze the function's behavior at the endpoints.
📏 Applying Calculus to Optimize a Cylinder's Volume
The sixth paragraph presents an application of the concepts discussed in the lecture by optimizing the volume of a cylinder given a constraint on the sum of its radius and height. The relationship between the volume 'v', the radius 'x', and the height 'y' is derived, and the process of finding the maximum volume by setting the derivative of 'v' with respect to 'x' to zero is explained. The importance of considering the domain of the function and the analytical approach over intuition is emphasized, with a comparison between the analytical solution and an intuitive one.
📈 The Interplay Between Analytical and Graphical Methods
The final paragraph wraps up the lecture by summarizing the key points and emphasizing the relationship between functions, derivatives, and graph plotting. It also discusses the importance of understanding the domain of a function and the computational role of related rates in dealing with max-min problems. The paragraph concludes with a reminder of the method to find high-low points of a function, which involves checking when the derivative is zero, where it fails to exist, and the endpoints if on a closed interval.
Mindmap
Keywords
💡Maxima and Minima
💡Derivative
💡Open Interval
💡Closed Interval
💡Continuous Function
💡Neighborhood
💡First and Second Derivatives
💡Critical Points
💡False Converses
💡Endpoint
💡Volume Optimization
Highlights
Introduction to the concept of maxima and minima in both analytical and geometric perspectives.
Fundamental theorem for studying maxima minima: If 'f of c' is at least as great as 'f of x' for all 'x' in a delta neighborhood of 'c' and 'f prime of c' exists, then 'f prime of c' must be 0.
Geometric interpretation of the fundamental theorem using the concept of open intervals and the behavior of a curve's derivative.
Illustration of how a positive derivative indicates a rising curve, which cannot represent a maximum point.
The importance of considering 'local' or 'relative' maxima and minima in addition to 'absolute' ones, with practical implications.
Three commandments as cautions against misinterpreting the theorem, including the risk of false converses.
Example demonstrating a curve with a horizontal tangent ('f prime of c' is 0) that does not represent a local maximum or minimum.
Discussion on the significance of the existence of 'f prime of c' and its relation to relative high and low points.
The difference between open and closed intervals in the context of finding maxima and minima, with emphasis on the domain of functions.
Explanation of how a continuous function on a closed interval must take on its maximum and minimum values somewhere on that interval.
The necessity to check endpoints in a closed interval for potential maxima and minima when the interior does not yield any candidates.
Application of the maxima and minima theory to a practical problem of optimizing the volume of a cylinder given a constraint on the sum of its radius and height.
Demonstration of how analytical methods can lead to counterintuitive results compared to more intuitive approaches, as shown in the cylinder volume optimization.
The analytical process of finding the maximum volume of a cylinder by setting the derivative of the volume function equal to zero and solving for 'x'.
Graphical representation of the volume function and its derivative, illustrating the location of maxima and the effect of the domain on the function's behavior.
The role of related rates in computational max-min problems and how they can be used without explicitly expressing one variable in terms of another.
Summary of the steps to find high-low points of a function, emphasizing the importance of checking when the derivative is zero, where it doesn't exist, and checking endpoints for closed intervals.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: