Calculus Chapter 1 Lecture 9 BONUS

Penn Online Learning
23 Jun 201612:13
EducationalLearning
32 Likes 10 Comments

TLDRIn this lecture, Professor Greist explores growth rates of functions, introducing the concept of Big O notation. He explains its significance in describing and controlling the growth of functions as they approach infinity or zero. The lecture touches on factorial functions, their extension to non-integer values, and the gamma function. Professor Greist also discusses the practical applications of Big O in computational complexity and error analysis, emphasizing its importance in both pure and applied mathematics. He concludes with examples, including the prime number theorem and Stirling's formula, demonstrating the versatility of Big O notation.

Takeaways
  • 🧑‍🏫 The lecture discusses the growth rates of functions, introducing a hierarchy of growth as x approaches infinity and zero.
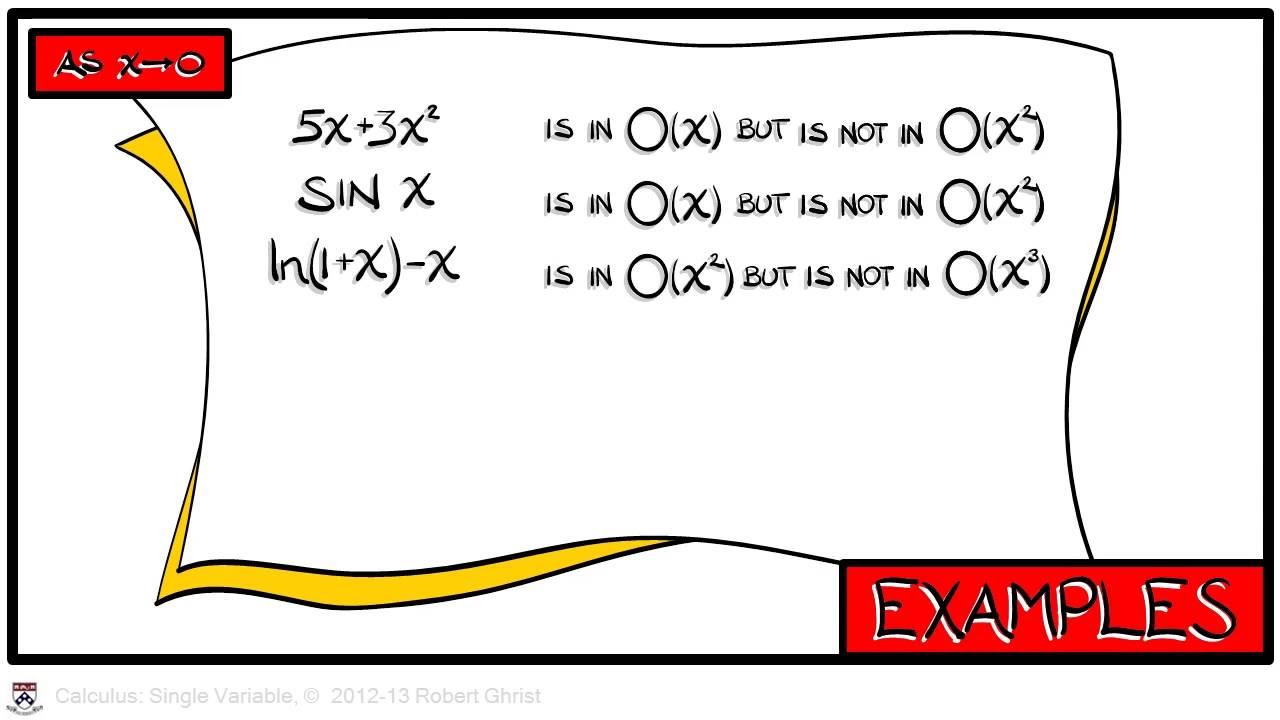
  • 🌀 Big O notation is introduced as a language to describe and control the growth of functions.
  • ❗ The factorial function is explored, including its definition for non-integer values using an integral from 0 to infinity.
  • 🔢 It's noted that factorial growth outpaces exponential growth as x approaches infinity.
  • 🔍 The gamma function is mentioned as related to the definition of the factorial function for non-integer values.
  • 📏 Big O notation is useful for describing the upper bounds of functions and is widely used in applied mathematics.
  • 💻 Big O notation has significant applications in computer science, particularly in computational complexity.
  • ⚙️ An example of algorithm complexity is given, explaining how multiplying two n-digit numbers can be described by Big O of n squared.
  • 🔬 Error analysis in engineering and physics can benefit from Big O notation to determine leading order terms in measurements.
  • 📈 Stirling's formula is introduced to describe the growth rate of x factorial, showcasing an advanced use of Big O notation.
Q & A

  • What is the main focus of the lecture?

    -The main focus of the lecture is on growth rates of functions, the concept of Big O notation, and factorial growth.

  • What is the real definition of the factorial function when X is not an integer?

    -The real definition of X factorial for non-integer X is given by the integral: ∫ (from 0 to ∞) of (T^X * e^-T) dT.

  • How does the factorial function compare to exponential growth as X approaches infinity?

    -The factorial function grows much faster than exponential growth (e^X) as X approaches infinity.

  • What is Big O notation, and why is it important?

    -Big O notation is a mathematical notation used to describe the upper bound of a function's growth rate. It is important because it provides an efficient language to express how functions behave as their input size grows, particularly in fields like computer science and applied mathematics.

  • How is Big O notation used in computer science?

    -In computer science, Big O notation is used to describe the computational complexity of algorithms, specifying how the time or space requirements grow as the input size increases.

  • What is an example of an algorithm's complexity described using Big O notation?

    -An example is the standard algorithm for multiplying two n-digit numbers, which has a complexity of Big O(n^2), indicating a quadratic amount of effort as n increases.

  • How does Big O notation help in error analysis in physics?

    -In physics, Big O notation helps quantify the leading order term of an error, such as the error in kinetic energy measurement due to a small error in velocity, allowing for an understanding of how errors propagate.

  • What is Stirling's formula, and how is it related to factorial growth?

    -Stirling's formula provides an approximation for the factorial function's growth, stating that log(X!) ≈ X log(X) - X + O(log(X)), and a more precise form relates X! to (√(2πX))(X/e)^X with a Big O term for correction.

  • How is the function π(X) related to the prime number theorem?

    -The function π(X) represents the number of primes less than X, and the prime number theorem states that π(X) is asymptotically approximated by X/log(X), with corrections expressed in Big O notation.

  • What is a key aspect students should understand about Big O notation?

    -Students should understand that Big O notation focuses on the leading order behavior of a function's growth, ignoring constant factors and lower-order terms, making it a valuable tool for simplifying complex analysis.

Outlines
00:00
📈 Introduction to Growth Rates and Big O Notation

Professor Greist introduces the lecture on growth rates of functions and the Big O notation. The factorial function is revisited, and its definition through integration is briefly explained. The discussion highlights that factorial growth surpasses exponential growth as x approaches infinity. The gamma function is mentioned as a related topic. The importance of Big O notation in applied mathematics is emphasized, serving as a tool to describe the upper bound of function growth rates.

05:01
🖩 Computational Complexity and Big O Notation

The practical application of Big O notation in computer science is explored. The example of multiplying two n-digit numbers illustrates how Big O helps estimate the computational effort required for an algorithm. The complexity of the standard multiplication algorithm is discussed, showing it to be O(n^2). The utility of Big O notation in error analysis, especially in physics and engineering, is also highlighted through the example of kinetic energy calculation.

10:05
📚 Big O Notation in Pure Mathematics

Big O notation's relevance in pure mathematics is demonstrated through the example of counting prime numbers less than a given number x. The prime number theorem is introduced, stating that the number of primes is asymptotically x/log(x). This example showcases how Big O notation helps describe the density of prime numbers among natural numbers and emphasizes its widespread use across various mathematical and scientific disciplines.

Mindmap
Keywords
💡Factorial Function
The factorial function, denoted as x!, is a mathematical function that multiplies a given positive integer by all the positive integers less than it. In this video, Professor Greist explores how the factorial function can be extended to non-integer values using an integral definition, demonstrating its complex behavior beyond simple multiplication of integers. This concept is central to the discussion, as the factorial growth is shown to outpace exponential growth significantly.
💡Gamma Function
The Gamma function is a complex mathematical concept that extends the factorial function to real and complex numbers. It is defined through an integral from 0 to infinity and satisfies properties similar to factorials, such as Gamma(n) = (n-1)! for positive integers. Professor Greist hints at this function as a more advanced topic in the course, explaining that it aligns with the integral definition of factorials, thus offering a consistent way to define factorial growth for non-integer values.
💡Exponential Growth
Exponential growth refers to the increase in quantity where the growth rate becomes more rapid in proportion to the growing total number or size. In the lecture, exponential growth is compared to factorial growth, and it's demonstrated that factorial growth exceeds exponential growth as x approaches infinity. This is an important concept in understanding the behavior of functions as x increases, especially when considering the hierarchy of growth rates in mathematics.
💡Big O Notation
Big O notation is a mathematical notation used to describe the upper bound of the growth rate of a function. It provides a way to categorize functions according to their growth as x approaches a limit (such as infinity or zero). In this video, Big O is shown to be a critical tool in both pure and applied mathematics, allowing mathematicians to describe how one function dominates another in terms of growth. Professor Greist discusses its application in computational complexity, error analysis, and the analysis of factorial and exponential functions.
💡Computational Complexity
Computational complexity is the study of the resources required to solve computational problems, typically time or space. The lecture uses the example of multiplying two n-digit numbers to illustrate how Big O notation can describe the efficiency of algorithms. This complexity analysis allows computer scientists to estimate how performance scales with input size, which is essential for evaluating the feasibility of algorithms as problems grow larger.
💡Stirling's Approximation
Stirling's Approximation is a formula used to approximate factorials for large values of x. It provides a more manageable expression for x! and is represented as: log(x!) ≈ x log(x) - x, plus a remainder term. This approximation is significant in mathematics, particularly in probability and combinatorics, as it gives insight into the growth rate of the factorial function and how it behaves asymptotically. Professor Greist references Stirling's Approximation to demonstrate a practical method for approximating factorial growth.
💡Prime Number Theorem
The Prime Number Theorem describes the asymptotic distribution of prime numbers among the positive integers. It states that the number of primes less than a given number x approximates x/log(x). In this lecture, Professor Greist uses the Prime Number Theorem to demonstrate how Big O notation can succinctly express mathematical truths about the density of primes, highlighting how primes become less frequent as numbers grow larger. The theorem illustrates a key application of Big O in pure mathematics.
💡Error Analysis
Error analysis is the process of assessing the uncertainty or error in mathematical computations and measurements. The video illustrates error analysis through the kinetic energy formula, examining how small errors in velocity measurement (epsilon) affect the overall kinetic energy calculation. By expanding the expression and identifying leading-order terms in epsilon, Professor Greist shows how Big O notation can help identify dominant error terms, aiding scientists and engineers in understanding and mitigating errors in real-world applications.
💡Hierarchy of Growth Rates
The hierarchy of growth rates is a conceptual framework used to compare the growth of various functions as x approaches infinity or zero. This concept allows mathematicians to understand which functions grow faster than others, providing a language to discuss their relative behavior. The lecture places particular emphasis on factorial and exponential growth, demonstrating that factorial functions grow more rapidly than exponential ones, establishing an order within this hierarchy.
💡Algorithm Efficiency
Algorithm efficiency refers to the computational resources, such as time and space, required by an algorithm to process data. Professor Greist uses the multiplication of two n-digit numbers to illustrate how Big O notation can express the efficiency of algorithms, estimating the work involved as input size increases. By categorizing algorithms into classes like O(n²) or O(n log n), Big O helps determine which algorithms are more efficient and suitable for particular tasks, highlighting its significance in computer science.
Highlights

Introduction to growth rates of functions and their hierarchy as X goes to infinity.

Definition and importance of Big O notation in discussing and controlling growth.

Reconsideration of the factorial function and its definition for non-integer values.

Explanation of the real definition of X factorial involving an integral.

Comparison of factorial growth to exponential growth, emphasizing that factorial growth is faster.

Introduction to the gamma function as a related concept to factorials.

Discussion on how Big O notation is used in applied mathematics and computational complexity.

Example of using Big O to describe the effort needed to multiply two n-digit numbers.

Application of Big O in error analysis in engineering and physics.

Introduction to Sterling's formula for determining the growth rate of X factorial.

Discussion on the usefulness of Sterling's formula in various fields like probability and combinatorics.

Pure mathematics application: Using Big O to state the prime number theorem.

Explanation of how Big O helps in understanding the density of prime numbers within natural numbers.

Encouragement to practice problems involving Big O notation to get used to the concept.

Summary of the importance of Big O notation across pure and applied mathematics, physical and computational sciences.

Transcripts

Browse More Related Video

Calculus Chapter 1 Lecture 9 Orders of Growth

Lec 36 | MIT 18.01 Single Variable Calculus, Fall 2007

Calculus Chapter 1 Lecture 8 l'Hopital's Rule

Calculus Chapter 2 Lecture 10 Derivatives

Calculus Chapter 4 Lecture 43 Probability Densities

Calculus Chapter 5 Lecture 45 Sequences II

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusMathematicsBig OFactorialsGrowth RatesAlgorithmsComputer ScienceTheoremGamma FunctionLecture