Work Energy Theorem: Block on a Slope
TLDRIn this educational video, Physics Ninja tackles the problem of a crate sliding down a ramp, exploring three methods to determine the crate's final speed. First, Newton's second law is applied to find acceleration, followed by kinematic equations. Finally, the Work-Energy Theorem is used, demonstrating its power in solving problems with multiple forces. The video includes step-by-step calculations, emphasizing the importance of understanding angles and force components in work calculations.
Takeaways
- 📚 The video is a physics lesson by 'Physics Ninja', focusing on a crate sliding down a ramp problem.
- 🔍 Two methods are discussed to solve the problem: Newton's second law and kinematics for finding acceleration, and the work-energy theorem for finding the final speed of the crate.
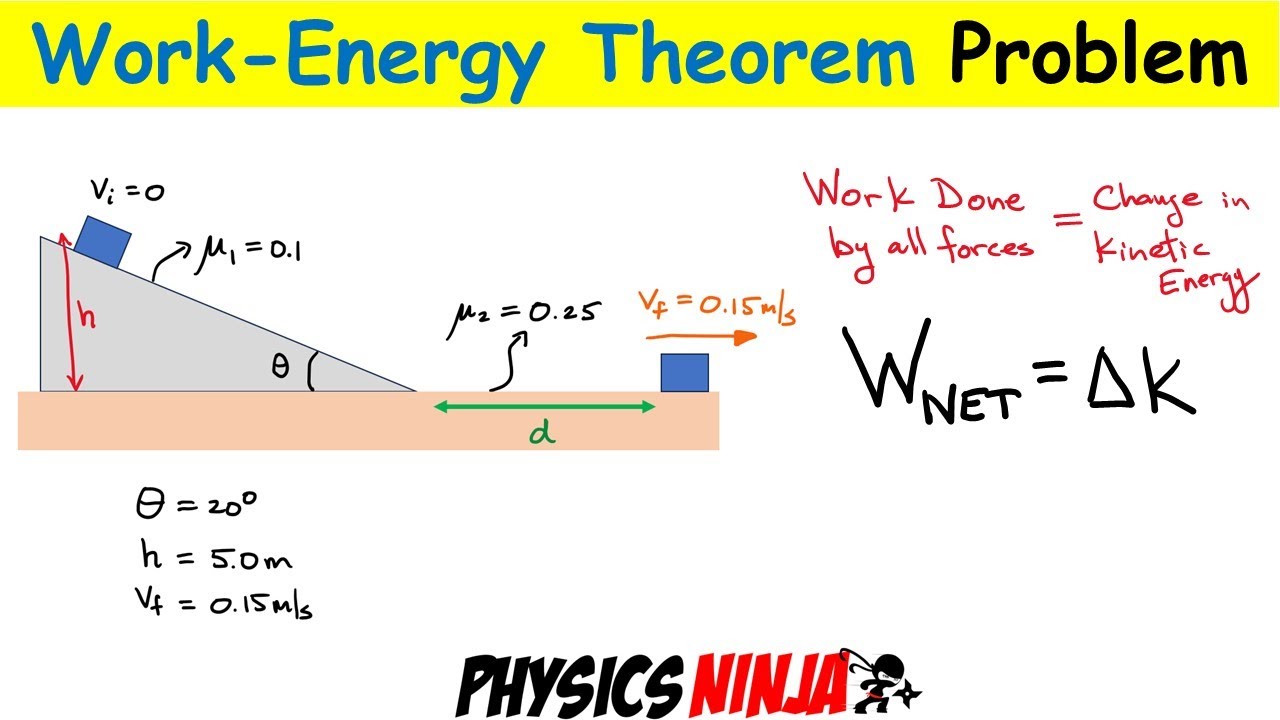
- 📐 The problem involves a 3 kg crate sliding down a 1-meter long ramp with a 30-degree angle, starting from rest, and subject to kinetic friction.
- 🧲 The coefficient of kinetic friction is provided, which is necessary for calculating the friction force acting on the crate.
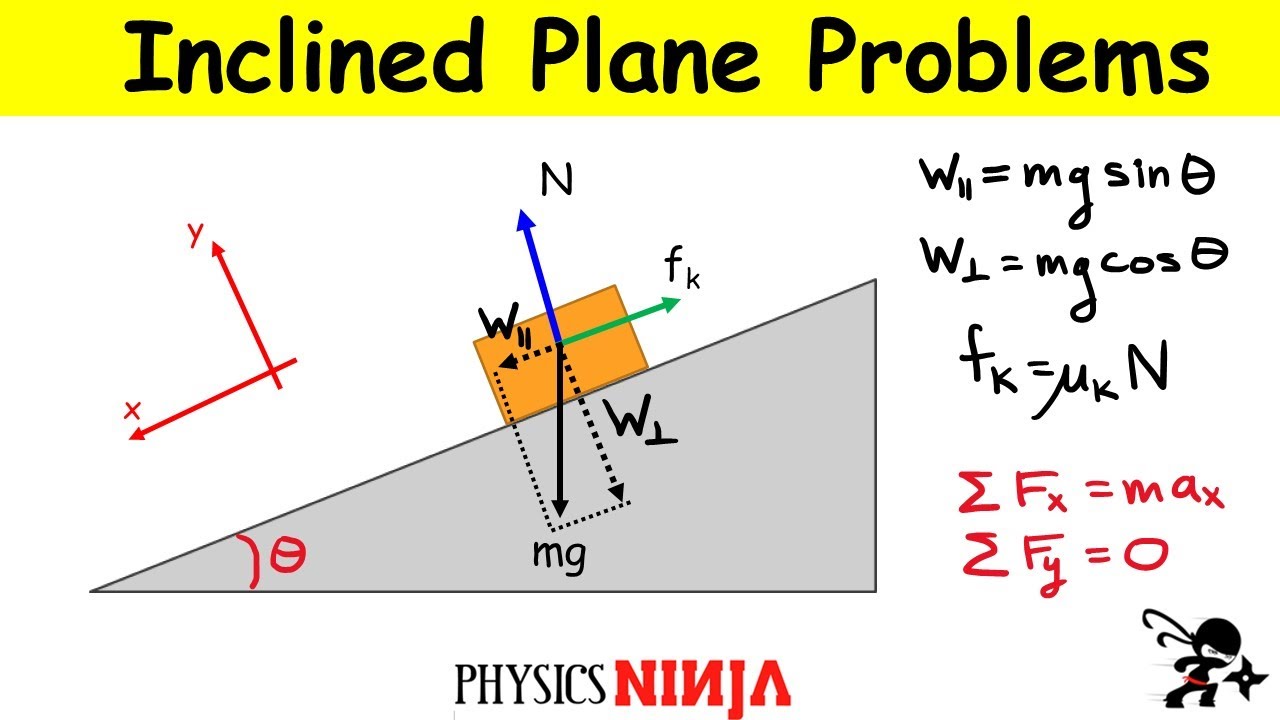
- 📈 The first step in solving the problem is to draw a free body diagram, identifying all forces acting on the crate, including weight, normal force, and friction.
- 📏 The normal force is calculated by considering the perpendicular component of the weight and the angle of the ramp.
- 🔄 Newton's second law is used to find the acceleration of the crate by summing forces along the ramp's direction and equating it to mass times acceleration.
- 📉 The friction force is determined by multiplying the coefficient of kinetic friction by the normal force.
- ⏱ Kinematic equations are used to relate the final velocity of the crate to its initial velocity, acceleration, and displacement.
- 🌐 The work-energy theorem is applied by calculating the work done by gravity and friction, and equating it to the change in kinetic energy of the crate.
- 🔢 The final speed of the crate is calculated using both methods, resulting in the same answer, demonstrating the consistency of physics principles.
Q & A
What are the two methods used to solve the crate sliding down a ramp problem?
-The two methods used are Newton's Second Law combined with kinematics, and the Work-Energy Theorem.
What is the initial setup of the problem involving the crate sliding down the ramp?
-The setup involves a 3 kg crate sliding down a 1-meter long ramp at an angle of 30 degrees, starting from rest with a coefficient of kinetic friction given.
How do you draw the free body diagram for the crate on the ramp?
-The free body diagram includes the weight (mg) acting downwards, the normal force acting perpendicular to the ramp, and the kinetic friction force acting opposite to the direction of motion along the ramp.
How is the normal force calculated in this problem?
-The normal force is calculated using the component of the weight perpendicular to the ramp: N = mg cos(30°). Substituting the values, N = 3 × 9.8 × cos(30°) = 25.5 N.
How is the kinetic friction force determined?
-The kinetic friction force is determined using the formula Fk = μk × N, where μk is the coefficient of kinetic friction and N is the normal force. Substituting the values, Fk = 0.15 × 25.5 = 3.8 N.
How is the acceleration of the crate calculated using Newton's Second Law?
-The acceleration is calculated by summing the forces along the x-direction and using Newton's Second Law: m a = mg sin(30°) - Fk. Simplifying, a = g (sin(30°) - μk cos(30°)). Substituting the values, a = 9.8 × (0.5 - 0.15 × 0.866) = 3.6 m/s².
How is the final speed of the crate determined using kinematics?
-Using the kinematic equation v² = u² + 2a d, where u = 0, a = 3.6 m/s², and d = 1 m. The final speed v = √(2 × 3.6 × 1) = 2.7 m/s.
What is the Work-Energy Theorem and how is it applied here?
-The Work-Energy Theorem states that the net work done on an object is equal to its change in kinetic energy. It is applied by calculating the work done by gravity and friction, summing these to find the net work, and equating this to the change in kinetic energy to find the final speed.
How do you calculate the work done by gravity in this scenario?
-The work done by gravity is Wg = mg cos(60°) × d. Substituting the values, Wg = 3 × 9.8 × cos(60°) × 1 = 14.7 J.
How do you calculate the work done by the kinetic friction force?
-The work done by the kinetic friction force is Wf = -Fk × d = -3.8 × 1 = -3.8 J.
What is the final speed of the crate using the Work-Energy Theorem?
-The net work done is the sum of the work done by gravity and friction: Wnet = 14.7 - 3.8 = 10.9 J. Using Wnet = ΔKE = ½ m v², solving for v gives v = √(2 × 10.9 / 3) = 2.7 m/s.
Outlines
📚 Introduction to Crate Sliding Down a Ramp Problem
The video begins with an introduction to a physics problem involving a crate sliding down a ramp. The presenter, Physics Ninja, outlines the plan to solve the problem using Newton's second law to find acceleration and kinematics to determine the final speed of the crate. Additionally, the work-energy theorem will be applied to solve the problem considering multiple forces. The video encourages viewers to support the channel by liking and subscribing. The problem involves a 3 kg crate sliding down a 1-meter long ramp at a 30-degree angle from rest, with friction accounted for using the coefficient of kinetic friction.
🔍 Setting Up the Free Body Diagram and Finding Normal Force
The presenter proceeds to draw a free body diagram for the crate, identifying the forces acting on it: weight, normal force, and kinetic friction. The weight is decomposed into components parallel and perpendicular to the ramp. The normal force is then calculated using the perpendicular component of the weight, which is found to be 25.5 Newtons. The kinetic friction force is determined using the coefficient of kinetic friction (0.15) and the normal force, resulting in approximately 3.8 Newtons.
🚀 Applying Newton's Second Law to Find Acceleration
Using Newton's second law, the presenter calculates the acceleration of the crate down the ramp. The forces along the x-direction (parallel to the ramp) are summed, considering the weight component parallel to the ramp and the opposing force of kinetic friction. The acceleration is found to be approximately 3.6 meters per second squared after substituting the values for mass, gravitational acceleration, and the coefficients.
📐 Solving for Speed Using Kinematics and Work-Energy Theorem
The presenter then addresses the main goal of the problem: finding the speed of the crate at the bottom of the ramp. Two methods are used: basic kinematics and the work-energy theorem. The kinematic approach uses the constant acceleration and displacement to find the final velocity, resulting in approximately 2.7 meters per second. The work-energy theorem is then introduced, emphasizing the calculation of work done by constant forces and setting up the equation to solve for the final speed.
🔧 Calculating Work Done by Forces and Final Speed
The final part of the video focuses on applying the work-energy theorem to find the crate's speed. The work done by gravity, friction, and the normal force is calculated, considering the angles between the forces and the displacement vector. The work done by the normal force is zero due to the 90-degree angle, and the work done by friction is negative. The work done by gravity is calculated using the 60-degree angle between the force of gravity and the displacement. The final speed is then found by solving the work-energy equation, confirming the earlier result of approximately 2.7 meters per second.
Mindmap
Keywords
💡Physics Ninja
💡Crate Sliding Down a Ramp
💡Newton's Second Law
💡Kinematics
💡Work-Energy Theorem
💡Free Body Diagram
💡Normal Force
💡Friction Force
💡Acceleration
💡Displacement
💡Kinetic Friction Coefficient
Highlights
The video explores the crate sliding down a ramp problem using Newton's second law and kinematics.
Introduction of the work-energy theorem as a method to solve for the crate's speed at the bottom of the ramp.
A three-kilogram crate sliding down a ramp with a length of one meter and a 30-degree angle.
The crate starts from rest, implying an initial velocity of zero.
The problem incorporates kinetic friction with a given coefficient.
Drawing a free body diagram to visualize forces acting on the crate.
Identifying the normal force and its calculation based on the coordinate system chosen.
Breaking down the weight of the crate into components parallel and perpendicular to the ramp.
Calculating the normal force using the perpendicular component of the weight.
Determining the friction force using the coefficient of kinetic friction and the normal force.
Applying Newton's second law to find the crate's acceleration down the ramp.
Using kinematic equations to relate acceleration, initial velocity, and displacement for calculating final velocity.
Solving for the crate's speed at the bottom of the ramp using basic kinematics.
Recalling the concept of work done by a constant force and its calculation.
Applying the work-energy theorem to find the final speed of the crate.
Calculating the work done by gravity, normal force, and friction force on the crate.
The work-energy theorem simplifies to a single equation for finding the crate's speed.
The video concludes by demonstrating the power of the work-energy theorem in solving complex problems with multiple forces.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: